Bentrokan inelastik dalam dimensi dan contoh

Itu Guncangan tidak elastis Atau tabrakan tidak elastis adalah interaksi yang singkat dan intens antara dua objek di mana jumlah gerakan dipertahankan, tetapi bukan energi kinetik, di mana persentase diubah menjadi beberapa jenis energi lainnya.

Guncangan atau tabrakan sering di alam. Partikel subatomik bertabrakan dengan kecepatan sangat tinggi, sementara banyak olahraga dan permainan terdiri dari tabrakan berkelanjutan. Bahkan galaksi mampu bertabrakan.

Gambar 1. Tabrakan mobil uji. Sumber: Pixabay

Sebenarnya jumlah gerakan dipertahankan dalam segala jenis tabrakan, selama partikel bertabrakan oleh sistem yang terisolasi. Jadi dalam hal ini tidak ada masalah. Sekarang, benda memiliki energi kinetik yang terkait dengan gerakan yang mereka miliki. Apa yang bisa terjadi dengan energi itu saat mogok?

Kekuatan internal yang terjadi selama bentrokan antara benda -benda itu intens. Ketika dinyatakan bahwa energi kinetik tidak dipertahankan, itu berarti bahwa ia diubah menjadi jenis energi lain: misalnya, dalam energi suara (tabrakan perangkat memiliki suara yang khas).

Lebih banyak kemungkinan penggunaan energi kinetik: panas dengan gesekan, dan tentu saja deformasi yang tak terhindarkan yang diderita oleh benda saat bertabrakan, seperti badan mobil pada gambar di atas.

[TOC]

Contoh tabrakan inelastik 

- Dua massa plastisin yang bertabrakan dan bertemu bersama, bergerak seperti satu bagian setelah kecelakaan.

- Bola karet yang memantul di dinding atau lantai. Bola cacat saat mempengaruhi permukaan.

Tidak semua energi kinetik diubah menjadi jenis energi lain, kecuali dalam beberapa pengecualian. Objek dapat tetap dengan sejumlah energi ini. Nanti kita akan melihat bagaimana menghitung persentase.

Ketika potongan -potongan yang bertabrakan dikaitkan, tabrakan disebut sempurna tidak elastis, dan keduanya biasanya berakhir bersatu.

Tabrakan yang sangat tidak elastis dalam dimensi

Tabrakan gambar menunjukkan dua objek dari massa yang berbeda M₁ Dan M₂, bergerak satu sama lain dengan kecepatan v_I1 Dan v_I2 masing -masing. Semuanya terjadi pada horizontal, yaitu, itu adalah tabrakan dalam dimensi, yang paling sederhana untuk dipelajari.

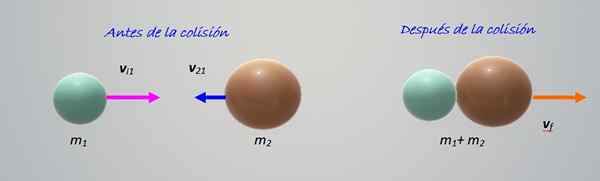Gambar 2. Tabrakan antara dua partikel dari massa yang berbeda. Sumber: Made sendiri.

Objek bertabrakan dan kemudian bersatu bergerak ke kanan. Ini adalah tabrakan yang sangat tidak elastis, jadi sudah cukup bahwa kita menjaga jumlah gerakan:

P_{salah satu} = P_F

Jumlah gerakan adalah vektor yang unitnya n.S. Dalam situasi yang dijelaskan, notasi vektor dapat dikeluarkan karena tabrakan dalam dimensi:

Ini dapat melayani Anda: Eksperimen Fisika Mudah (Universitas Primer)

MV_{salah satu} = MV_F

Jumlah pergerakan sistem adalah jumlah vektor dari jumlah pergerakan masing -masing partikel.

M₁ v_I1  + M₂ v_I2 = (m₁ + M₂) v_F

Kecepatan terakhir diberikan oleh:

v_F = (m₁ v_I1  + M₂ v_I2)/ (M₁ + M₂)

Koefisien restitusi

Ada jumlah yang dapat menunjukkan seberapa elastisnya tabrakan. Ini tentang koefisien restitusi, yang didefinisikan sebagai rasio negatif antara kecepatan relatif partikel setelah kecelakaan dan kecepatan relatif sebelum kecelakaan.

Biarkan u₁ dan kamu₂ Kecepatan masing -masing partikel. Dan jadilah v₁ dan v₂ Kecepatan akhir masing -masing. Secara matematis koefisien restitusi dapat dinyatakan sebagai berikut:

Koefisien restitusi adalah jumlah tambahan, karena itu adalah rasio antara kecepatan. Tetapi informasi yang diberikan sangat menarik:

- Jika ε = 0 setara dengan menyatakan itu v₂ = v₁. Itu berarti bahwa kecepatan akhir adalah sama dan bentrokannya tidak elastis, seperti yang dijelaskan pada bagian sebelumnya.

- Ketika ε = 1 berarti kecepatan relatif baik sebelum dan sesudah kecelakaan tidak berubah, dalam hal ini bentrokannya elastis.

- Dan jika 0 < ε < 1 parte de la energía cinética de la colisión se transforma en alguna otra de las energías mencionadas anteriormente.

Bagaimana menentukan koefisien restitusi?

Koefisien restitusi tergantung pada kelas bahan yang terlibat dalam tabrakan. Tes yang sangat menarik untuk menentukan seberapa elastis bahan untuk membuat bola adalah menjatuhkan bola pada permukaan yang tetap dan mengukur ketinggian rebound.

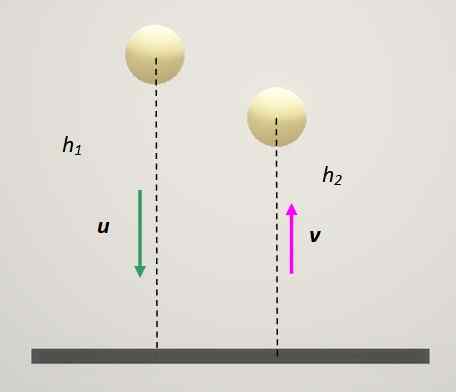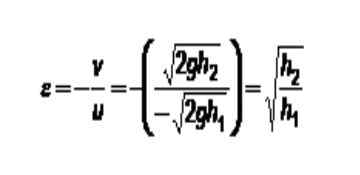
Gambar 3. Metode untuk menentukan koefisien restitusi. Sumber: Made sendiri.

Dalam hal ini pelat tetap selalu memiliki kecepatan 0. Jika indeks 1 ini ditugaskan untuk ini dan bola adalah: Indeks 2 tetap:

Kecepatan awal tergantung pada ketinggian H₁ dari mana dia menjatuhkan:

Tanda negatif menunjukkan arah turun. Dan kecepatan akhir terkait dengan ketinggian maksimum H₂ yang mencapai rebound:

Mengganti koefisien restitusi yang Anda miliki:

Ledakan

Pada awalnya telah disarankan bahwa semua energi kinetik dapat diubah dengan pindah ke jenis energi lainnya. Bagaimanapun, energi tidak hancur. Mungkinkah benda -benda yang datang dengan gerakan bertabrakan dan bergabung bersama membentuk satu objek yang tiba -tiba sedang istirahat? Ini tidak begitu mudah untuk dibayangkan.

Itu dapat melayani Anda: Dinamika: Sejarah, Studi, Hukum, dan Teori Apa

Namun, mari kita bayangkan apa yang terjadi mundur, seperti dalam film yang terlihat di belakang. Kemudian objek awalnya beristirahat dan kemudian meledak fragmentasi menjadi beberapa bagian. Situasi ini sangat mungkin: ini adalah ledakan.

Sehingga ledakan dapat dianggap sebagai tabrakan tidak elastis yang dilihat ke belakang tepat waktu. Jumlah gerakan juga dipertahankan, mampu menegaskan itu:

P_{salah satu} = P_F

Contoh terpecahkan

-Latihan 1

Diketahui dari pengukuran bahwa koefisien restitusi baja adalah 0.90. Bola baja dijatuhkan dari tinggi 7 m di atas pelat tetap. Menghitung:

a) Sampai ketinggian berapa memantul.

b) Berapa lama waktu yang dibutuhkan antara kontak pertama dengan permukaan dan yang kedua.

Larutan

a) Persamaan yang sebelumnya disimpulkan di bagian tentang penentuan koefisien restitusi digunakan:

Tinggi Bersih H₂:

0.90² . 7 m = 5.67 m

b) untuk menaikkan 5.67 meter kecepatan yang diberikan oleh:

Darimana:

Dan waktu yang diperlukan untuk mencapai ketinggian ini adalah:

T _Max = v_{salah satu}/ g = (10.54/9.8 s) = 1.08 s.

Waktu yang diperlukan untuk kembali adalah sama, oleh karena itu total waktu untuk mengunggah 5.67 meter dan kembali ke titik awal adalah dua kali waktu maksimum:

T_penerbangan = 2.15 s.

-Latihan 2

Gambar tersebut menunjukkan blok kayu massa yang tergantung pada sisa benang dengan panjang l sebagai pendulum. Ini disebut pendulum balistik dan berfungsi untuk mengukur kecepatan v masuk massa massa m. Semakin tinggi kecepatan peluru yang berdampak pada blok, pada ketinggian yang lebih tinggi ini akan dibangun.

Bullet gambar tertanam di blok, oleh karena itu adalah guncangan yang benar -benar tidak elastis.

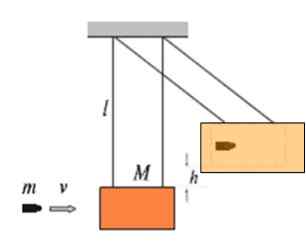Gambar 4. Pendulum balistik.

Asumsikan bahwa 9 9.72 g Dampak terhadap Blok Massa 4.60 kg, lalu set naik menjadi 16.8 cm dari posisi ekuilibrium. Berapa kecepatannya v dari peluru?

Larutan

Selama tabrakan jumlah gerakan dipertahankan dan atau_F Ini adalah kecepatan set, setelah peluru tertanam di blok:

P_{salah satu} = P_F

Blok awalnya beristirahat, sedangkan peluru diarahkan ke target dengan kecepatan v:

M.v + m.0 = (m + m) u_F

 

Tidak diketahui atau_F Bahkan, tetapi setelah tabrakan, energi mekanik dipertahankan, ini adalah jumlah energi potensial gravitasi dan energi kinetik K:

Dapat melayani Anda: jumlah vektor: metode grafis, contoh, latihan terpecahkan

Energi mekanik awal = energi mekanik akhir

DAN_mo = E_Mf

ATAU_{salah satu} + K_{salah satu} = U_F + K_F

Energi potensial gravitasi tergantung pada ketinggian di mana set mencapai. Untuk posisi ekuilibrium, ketinggian awal adalah yang diambil sebagai tingkat referensi, oleh karena itu:

ATAU_{salah satu} = 0

Berkat peluru, set memiliki energi kinetik K_{salah satu}, yang menjadi energi potensial gravitasi saat set mencapai ketinggian maksimum H. Energi kinetik diberikan oleh:

K = ½ mV²

Awalnya energi kinetik adalah:

K_{salah satu} = (1/2) (m+m) u_F²

Ingatlah bahwa peluru dan blok membentuk satu objek massa tunggal M+ m. Energi potensial gravitasi ketika mereka telah mencapai pada ketinggian maksimum adalah:

ATAU_F = (m + m) GH

Karena itu:

K_{salah satu} = U_F

(1/2) (m+m) u_F² = (m + m) GH

Sekarang hasil ini diganti dalam ekspresi untuk v yang dibersihkan di awal, dari konservasi jumlah gerakan:

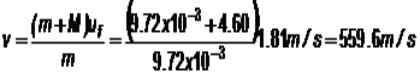
-Latihan 3

Objek gambar meledak dalam tiga fragmen: dua massa m yang sama dan satu massa yang lebih besar 2m. Gambar menunjukkan kecepatan masing -masing fragmen setelah ledakan. Apa tujuan awal objek?

Gambar 5. Batu yang meledak dalam 3 fragmen. Sumber: Made sendiri.

Larutan

Masalah ini membutuhkan penggunaan dua koordinat: X Dan Dan, Karena dua fragmen memiliki kecepatan vertikal, sedangkan sisanya memiliki kecepatan horizontal.

Massa total objek adalah jumlah massa semua fragmen:

M = m + m + 2m = 4m

Jumlah gerakan dipertahankan baik pada sumbu x dan pada sumbu y, diusulkan secara terpisah:

1. 4m. atau_X= m v₃
2. 4m. atau_Dan = m. 2v₁ - 2m. v₁

Perhatikan bahwa fragmen besar bergerak ke bawah dengan kecepatan v1, untuk menunjukkan fakta ini tanda negatif telah ditempatkan.

Dari persamaan kedua segera mengikuti itu atau_Dan = 0, Dan yang pertama segera jelas UX:

Tujuan awal objek adalah u_{salah satu} = u_X = v₃/4.

Referensi

1. Giancoli, d.  2006. Fisika: Prinsip dengan aplikasi. 6^th. Ed Prentice Hall. 175-181
2. Rex, a. 2011. Dasar -dasar fisika. Pearson. 135-155.
3. Serway, r., Vulle, c. 2011. Dasar -dasar fisika. 9^na Pembelajaran Cengage. 172 -182
4. Tipler, hlm. (2006) Fisika untuk Sains dan Teknologi. Edisi ke -5. Volume 1. Editorial dikembalikan. 217-238
5. Tippens, hlm. 2011. Fisika: Konsep dan Aplikasi. Edisi ke -7. Bukit MacGraw. 185 -195