Sirkuit Listrik Campuran

Kami menjelaskan apa itu sirkuit campuran, karakteristiknya, bagian, simbol dan memberikan beberapa contoh

Apa itu sirkuit campuran?

Dia Sirkuit Listrik Campuran Ini adalah salah satu yang berisi elemen yang terhubung baik secara seri maupun paralel, sehingga, ketika menutup sirkuit, ketegangan dan arus yang berbeda ditetapkan di masing -masing.

Sirkuit dirancang dengan berbagai tujuan dan elemennya termasuk dalam dua kategori: aset dan kewajiban.

Elemen aktif dari sirkuit adalah generator atau tegangan atau sumber arus, langsung atau alternatif. Di sisi lain, elemen pasif adalah resistensi, kapasitor atau kapasitor dan kumparan. Baik satu dan yang lainnya mengakui koneksi secara seri dan paralel, serta kombinasi ini.

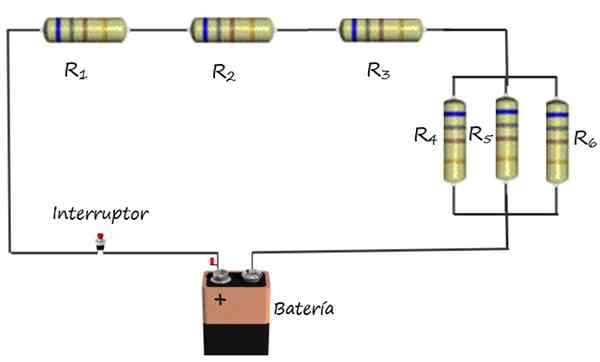
Gambar teratas menunjukkan, sebagai contoh, hubungan campuran hambatan listrik dengan baterai dan sakelar. Resistensi r₁, R₂ dan r₃ Mereka dikaitkan secara seri, sedangkan resistor r₄, R₅ dan r₆ Mereka terhubung secara paralel.

Koneksi lain yang mungkin, berbeda dari asosiasi serial-paralel, adalah delta (atau segitiga) dan bintang, sering digunakan dalam mesin listrik yang diberi makan dengan arus bolak-balik.

Karakteristik sirkuit campuran

Secara umum, berikut ini diamati di sirkuit campuran:

• Umpan sirkuit dapat melalui generator langsung (baterai) atau alternatif.
• Dianggap bahwa kabel atau kabel yang menyatukan elemen yang berbeda tidak menawarkan resistensi saat ini.
• Tegangan dan arus dapat konstan atau variabel dalam waktu. Huruf kapital digunakan untuk menunjukkan nilai konstan, dan huruf kecil saat variabel.
• Dalam sirkuit campuran murni resistif, resistensi deret arus melalui adalah sama, sedangkan dalam resistensi paralel secara umum itu berbeda. Untuk menghitung arus dan tegangan melalui setiap resistansi, sirkuit biasanya direduksi menjadi resistansi yang unik, disebut resistansi setara atau r_Persamaan .

Itu dapat melayani Anda: pengurangan vektor: metode grafis, contoh, latihan

Resistensi seri

Resistensi secara paralel

• Jika sirkuit terdiri dari kapasitor N, ketika kapasitansi setara C dikaitkan secara seri_Persamaan hasil:

Kapasitor Seri

Kapasitor paralel

• Kumparan atau induktor mengikuti aturan asosiasi yang sama dengan resistensi. Dengan demikian, ketika Anda ingin mengurangi asosiasi kumparan seri untuk mendapatkan induktansi setara l_Persamaan, Rumus berikut digunakan:

Induktor serial

Induktor secara paralel

• Untuk menyelesaikan sirkuit campuran dengan resistor, hukum Ohm dan undang -undang Kirchoff digunakan. Dalam sirkuit resistif sederhana, hukum Ohm sudah cukup, tetapi untuk jaringan yang lebih kompleks itu perlu hadir.

Hubungan antara tegangan dan arus

Bergantung pada elemen sirkuit, ada hubungan antara tegangan atau tegangan melalui elemen dengan intensitas arus yang melewati itu:

Resistensi r

Hukum Ohm digunakan:

v_R(t) = r ∙ i_R(T)

Kapasitor c

Induktansi l

Bagian dari sirkuit campuran

Dalam sirkuit listrik, bagian -bagian berikut dibedakan:

Simpul

Titik serikat antara dua atau lebih kabel konduktif yang menghubungkan beberapa aktif atau kewajiban sirkuit.

Cabang

Elemen, apakah aktif atau kewajiban, yang berada di antara dua knot berturut -turut.

Mesh

Bagian tertutup dari sirkuit berjalan tanpa melewati dua kali melalui titik yang sama. Itu mungkin atau mungkin tidak memiliki tegangan atau generator arus.

Hukum atau aturan kirchoff

Aturan kirchoff berlaku baik baik arus dan tegangan konstan atau jika mereka tergantung pada waktu. Meskipun mereka biasanya disebut hukum, mereka sebenarnya adalah aturan untuk menerapkan prinsip konservasi ke sirkuit listrik.

Dapat melayani Anda: fisika keadaan padat: sifat, struktur, contoh

Aturan pertama

Ini menetapkan prinsip konservasi beban, menunjukkan bahwa jumlah intensitas saat ini yang memasuki simpul, setara dengan jumlah intensitas yang keluar dari itu:

∑ i_{pintu masuk} = ∑ i_KELUAR

Aturan kedua

Pada kesempatan ini prinsip konservasi energi ditetapkan, ketika menyatakan bahwa jumlah aljabar dari ketegangan dalam bagian tertutup sirkuit (mesh) adalah nol.

∑ vi = 0

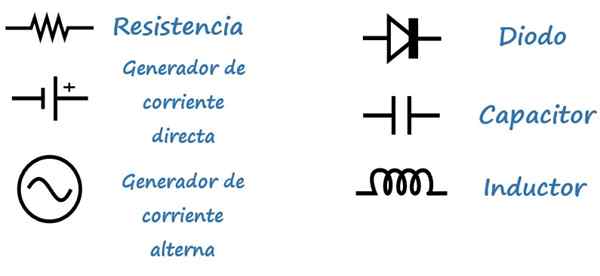
Simbol

Untuk memfasilitasi analisis sirkuit, simbol -simbol berikut digunakan:

Contoh sirkuit campuran

Contoh 1

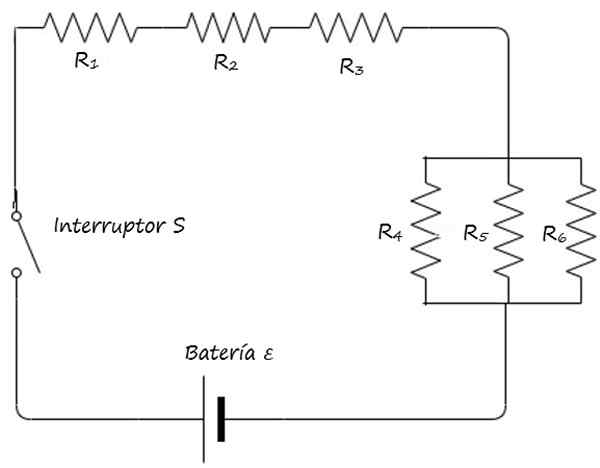
Gambarlah sirkuit campuran dari figur start compact, dengan menggunakan simbol yang dijelaskan di atas.

Menjawab

Contoh 2

Di sirkuit contoh 1 Anda memiliki nilai berikut untuk resistor dan baterai:

R₁ = 50 Ω; R₂ = 100 Ω; R₃ = 75 Ω, r₄ = 24 Ω, r₅ = 48 Ω; R₆ = 48 Ω; ε = 100 V

Untuk sirkuit yang ditunjukkan, baterai dianggap ideal, yaitu, tidak memiliki resistensi internal. Biasanya baterai asli memiliki resistansi internal kecil yang ditarik secara seri dengan baterai dan diperlakukan sama dengan resistensi lainnya di sirkuit.

Hitung yang berikut:

• a) resistansi yang setara dari sirkuit.
• b) nilai arus yang keluar dari baterai.
• c) tegangan dan arus di masing -masing resistensi.

Menjawab

Kelompok Perlawanan Pertama: R₁ = 50 Ω; R₂ = 100 Ω; R₃ = 75 Ω terhubung secara seri, oleh karena itu, resistansi yang setara adalah R₁₂₃:

R₁₂₃ = R₁ + R₂ + R₃ = 50 Ω + 100 Ω + 75 Ω = 225 Ω

Itu dapat melayani Anda: Hukum Ketiga Termodinamika: Rumus, Persamaan, Contoh

Adapun kelompok resistensi r₄ = 24 Ω, r₅ = 48 Ω; R₆ = 48 Ω, terhubung secara paralel dan rumus yang sesuai harus diterapkan:

 Buram timbal balik atau terbalik dari hasil sebelumnya adalah resistansi yang setara untuk grup:

R₄₅₆ = 12 Ω

Sirkuit yang disederhanakan yang diperoleh ditunjukkan dalam grafik berikut, terdiri dari dua resistensi seri dengan baterai atau baterai. Dua resistensi ini ditambahkan untuk menemukan resistansi setara dari sirkuit R asli_Persamaan:

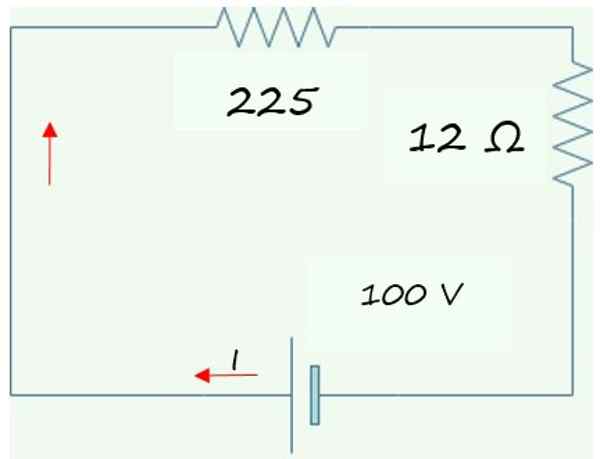
R_Persamaan= 225 Ω + 12 Ω = 237 Ω

Jawaban b

Arus yang meninggalkan baterai (dengan konvensi selalu ditarik oleh kutub positif) dihitung dengan sirkuit yang disederhanakan, yang terdiri dari resistansi setara R_Persamaan Seri dengan baterai, yang diterapkan oleh hukum Ohm:

ε = i · r

I = ε / r = 100 V / 237 Ω = 0.422 a

Jawaban c

Tegangan dan arus di masing -masing resistensi SA Hitung oleh hukum Ohm. Hal pertama yang diamati adalah bahwa arus yang keluar dari baterai benar -benar melintasi resistensi r₁ , R₂ dan r₃ Dan sebaliknya, itu dibagi dengan melintasi r₄ , R₅ dan r₆.

Tegangan v₁, V₂ dan v₃ adalah:

V₁  = 0.422 A × 50 Ω = 21.1 v
V₂  = 0.422 A × 100 Ω = 42.2 v
V₃  = 0.422 A × 75 Ω = 31.7 v

Untuk bagiannya, Voltajes v₄, V₅ dan v₆ Mereka memiliki nilai yang sama, karena resistensi secara paralel:

V₄ = V₅ = V₆ = 0.422 A × 12 Ω = 5.06 v

Dan arus masing -masing adalah:

yo₄ = 5.06 V / 24 Ω = 0.211 a

yo₅ = I₆ = 5.06 V / 48 Ω = 0.105 a

Perhatikan bahwa dengan menambahkan saya₄, yo₅ dan saya₆ Total arus yang keluar dari baterai diperoleh lagi.