Konsep Koefisien Konsepsi, Formula, Perhitungan, Contoh

Dia koefisien restitusi Itu adalah hasil bagi antara kecepatan ngebut relatif dan kecepatan relatif mendekati dua badan yang bertabrakan. Saat mayat disatukan setelah tabrakan, hasil bagi ini kosong. Dan unit ini bernilai jika tabrakannya sangat elastis.

Misalkan dua bidang massa padat M1 dan massa M2 masing -masing bahwa mereka menderita tabrakan. Tepat sebelum tabrakan, bola memiliki kecepatan V1 Dan V2 Mengenai sistem referensi inersia tertentu. Tepat setelah menabrak kecepatan mereka berubah menjadi V1 ' Dan V2 '.

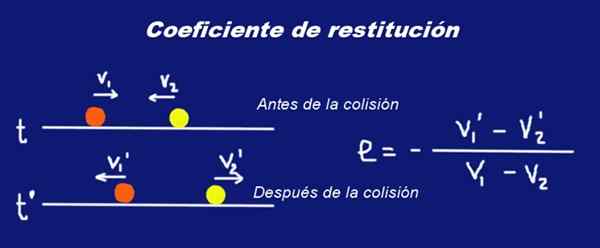Gambar 1. Tabrakan dua bidang massa M1 dan M2 dan koefisien restitusi mereka dan. Disiapkan oleh Ricardo Pérez.

Surat telah ditempatkan Huruf tebal Dalam kecepatan untuk menunjukkan bahwa mereka adalah jumlah vektor.

Eksperimen menunjukkan bahwa setiap tabrakan memenuhi hubungan berikut:

V1 ' - V2 '= -Dan (V1 - V2)

Di mana Dan Itu adalah bilangan real antara 0 dan 1, disebut koefisien restitusi dari tabrakan. Ekspresi sebelumnya ditafsirkan sebagai berikut: 

Kecepatan relatif dari dua partikel sebelum tabrakan sebanding dengan kecepatan relatif dari dua partikel setelah tabrakan, konstanta proporsionalitas adalah (-e), di mana E adalah koefisien ganti rugi dari tabrakan.

[TOC]

Untuk apa koefisien restitusi?

Kegunaan koefisien ini terletak pada mengetahui Tingkat inelastisitas dari tabrakan. Jika tabrakannya sangat elastis koefisiennya akan menjadi 1, sedangkan dalam tabrakan yang benar -benar tidak elastis koefisiennya akan bernilai 0, karena dalam hal ini, kecepatan relatif setelah tabrakan adalah nol.

Secara timbal balik, jika koefisien restitusi tabrakan dan kecepatan partikel diketahui sebelumnya, maka kecepatan dapat diprediksi setelah tabrakan tersebut terjadi. 

Dapat melayani Anda: 13 contoh hukum pertama Newton dalam kehidupan nyata

Momentumnya

Dalam tabrakan, selain hubungan yang ditetapkan oleh koefisien restitusi, ada hubungan mendasar lainnya, yang merupakan Konservasi Momentum.

Momentumnya P dari sebuah partikel, atau jumlah gerakan seperti yang disebut juga, itu adalah produk dari massa M partikel untuk kecepatannya V. Yaitu momentum P Itu adalah jumlah vektor.

Dalam tabrakan momentum linier P Sistem ini sama tepat sebelum dan tepat setelah tabrakan, karena gaya eksterior tercela melawan kekuatan interaksi internal yang singkat namun intens selama tabrakan. Tapi konservasi momentum tidak cukup P sistem untuk menyelesaikan masalah umum tabrakan.

Dalam kasus yang disebutkan sebelumnya, bahwa dari dua bola M1 dan M2 yang bertabrakan, konservasi momentum linier ditulis seperti ini:

 M1 V1 + M2 V2 = M1 V1 ' + M2 V2 ' .

Tidak ada cara untuk menyelesaikan masalah tabrakan jika koefisien restitusi tidak diketahui. Konservasi momentum, meskipun perlu, tidak cukup untuk memprediksi kecepatan setelah tabrakan.

Ketika masalah menyatakan bahwa tubuh bergerak bersama setelah tabrakan, secara implisit mengatakan bahwa koefisien restitusi adalah 0.

Gambar 2. Dalam bola biliar ada tabrakan koefisien restitusi sedikit kurang dari 1. Sumber: Pixabay.

Koefisien Energi dan Restitusi 

Jumlah fisik penting lainnya yang terlibat dalam tabrakan adalah energi. Selama tabrakan ada pertukaran energi kinetik, energi potensial dan jenis energi lainnya, seperti energi kalori.

Sebelum dan sesudah tabrakan energi interaksi potensial praktis nol, sehingga keseimbangan energi melibatkan energi kinetik partikel sebelum dan sesudah Q disebut energi yang hilang.

Itu bisa melayani Anda: model atom Heisenberg

Untuk dua bidang massa M1 dan M2 yang bertabrakan dengan keseimbangan energi sebelum dan sesudah tabrakan ditulis seperti ini:

½ M1 V1^2 + ½ m2 V2^2 = ½ m1 V1 '^2 + ½ m2 V2 '^2 + q

Ketika kekuatan interaksi selama tabrakan murni konservatif, itu terjadi itu Total energi kinetik Dari partikel yang bertabrakan diawetkan, yaitu, itu sama sebelum dan sesudah tabrakan (q = 0). Ketika ini terjadi, dikatakan bahwa tabrakan sangat elastis.

Dalam kasus tabrakan elastis, energi tidak hilang. Dan juga koefisien restitusi memuaskan: E = 1. 

Sebaliknya, dalam tabrakan inelastik yang ≠ 0 dan 0 ≤ e < 1. Sabemos, por ejemplo, que la colisión de las bolas de billar no es perfectamente elástica porque el sonido que se emite durante el impacto es parte de la energía disipada.

Agar masalah tabrakan ditentukan secara sempurna, perlu mengetahui koefisien restitusi, atau secara bergantian jumlah energi yang dihamburkan selama tabrakan.

Koefisien restitusi tergantung pada sifat dan jenis interaksi antara kedua badan selama tabrakan.

Di sisi lain, kecepatan relatif tubuh sebelum tabrakan akan menentukan intensitas interaksi dan karenanya pengaruhnya terhadap koefisien restitusi. 

Bagaimana koefisien restitusi dihitung?

Untuk mengilustrasikan bagaimana koefisien restitusi dari tabrakan dihitung, kami akan mengambil kasus sederhana:

Misalkan tabrakan dua bidang massa M1 = 1 kg Dan M2 = 2 kg Langkah itu pada gesekan lurus (seperti pada Gambar 1).

Lingkungan pertama mempengaruhi kecepatan awal V1 = 1 m/s Tentang yang kedua yang awalnya beristirahat, yaitu V2 = 0 m/s.

Ini dapat melayani Anda: Hukum Termodinamika Pertama: Rumus, Persamaan, Contoh

Setelah tabrakan mereka bergerak seperti ini: yang pertama berhenti (V1 '= 0 m/s) dan yang kedua bergerak ke kanan dengan kecepatan V2 '= 1/2 m/s.

Untuk menghitung koefisien restitusi dalam tabrakan ini, kami menerapkan hubungan:

V1 ' - V2 ' = -Dan ( V1 - V2 ) 

0 m/s - 1/2 m/s = - e (1 m/s - 0 m/s) => - 1/2 = - e => e = 1/2 .

Contoh

Dalam tabrakan satu dimensi dari dua bidang dari bagian sebelumnya, koefisien restitusi dihitung menghasilkan E = ½ .

Karena e ≠ 1 Tabrakannya tidak elastis, yaitu, energi kinetik sistem tidak dipertahankan dan ada sejumlah energi yang dihilangkan Q (misalnya pemanasan bola karena tabrakan).

Tentukan nilai energi yang hilang dalam joule. Juga menghitung persentase fraksi energi yang hilang.

Larutan

Energi kinetik awal Sphere 1 adalah: 

K1i = ½ m1 v1^2 = ½ 1 kg (1 m/s)^2 = ½ j

Sedangkan dari Sphere 2 adalah nol untuk awalnya sedang istirahat.

Jadi energi kinetik awal sistem adalah Ki = ½ J.

Setelah tabrakan hanya bola kedua bergerak dengan kecepatan v2 '= ½ m/s, sehingga energi kinetik akhir dari sistem adalah:

Kf = ½ m2 v2 '^2 = ½ 2 kg (½ m/s)^2 = ¼ j

Artinya, energi yang dihamburkan dalam tabrakan adalah:

Q = ki - kf = (½ j - ¼ j) = 1/4 j

Dan fraksi energi yang dihamburkan dalam tabrakan ini dihitung sebagai berikut:

F = q / ki = ¼ / ½ = 0,5 Artinya 50% energi sistem telah dihilang karena tabrakan inelastik yang koefisien restitusi adalah 0,5.

Referensi

1. Bauer, w. 2011. Fisika untuk Teknik dan Ilmu Pengetahuan. Volume 1. MC Graw Hill.
2. Figueroa, d. 2005. Seri: Fisika untuk Sains dan Teknik. Volume 1. Kinematika. Diedit oleh Douglas Figueroa (USB).
3. Knight, r. 2017. Fisika untuk Ilmuwan dan Teknik: Pendekatan Strategi. Pearson.
4. Sears, Zemansky. 2016. Fisika Universitas dengan Fisika Modern. 14. Ed. Volume 1.
5. Wikipedia. Jumlah gerakan.Pulih dari: is.Wikipedia.org.