Kongruensi Angka Kongruen, Kriteria, Contoh, Latihan

Itu kesesuaian, Dalam geometri, ia menunjukkan bahwa jika dua figur datar memiliki bentuk dan dimensi yang sama, ini kongruen. Misalnya, dua segmen kongruen saat panjangnya sama. Sudut yang kongruen juga memiliki ukuran yang sama, meskipun tidak berorientasi pada cara yang sama di pesawat.

Istilah "kongruensi" berasal dari bahasa Latin Kongruentia, yang artinya korespondensi. Dengan demikian, dua tokoh kongruen berhubungan persis satu dengan yang lain.

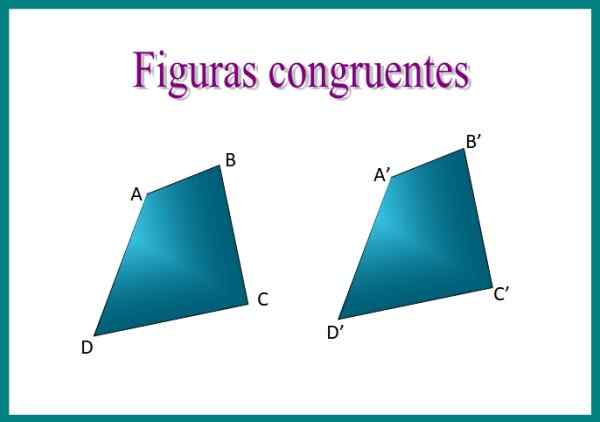
Gambar 1. ABCD Quadrilaterals dan A'B'C'D 'dari sosok itu kongruen: Sisi mereka memiliki ukuran yang sama, serta sudut internal mereka. Sumber: f. Zapata.

Misalnya, jika kita tumpang tindih dua segi empat dari gambar, kita akan menemukan bahwa mereka kongruen, karena disposisi sisi mereka identik dan mereka mengukur hal yang sama.

Saat menempatkan quadrilateral ABCD dan A'B'C'D 'satu di yang lain, angkanya akan bertepatan dengan tepat. Sisi yang cocok dipanggil Sisi homolog salah satu sesuai Dan untuk mengekspresikan kesesuaian simbol ≡ digunakan. Kemudian kita dapat mengatakan bahwa ABCD ≡ a'b'c'd '.

[TOC]

Kriteria Kongruensi

Karakteristik berikut adalah umum untuk poligon kongruen:

-Bentuk dan ukuran yang sama.

-Langkah -langkah identik dari sudut Anda.

-Tingkat yang sama di masing -masing sisinya.

Dalam hal dua poligon yang dipertanyakan secara teratur, yaitu, bahwa semua pihak dan sudut internal mengukur hal yang sama, kongruensi dijamin ketika salah satu kondisi berikut dipenuhi:

-Sisinya kongruen

-Itu apothem memiliki ukuran yang sama

-Dia radio dari setiap poligon mengukur hal yang sama

Apothem dari poligon biasa adalah jarak antara pusat dan salah satu sisi, sedangkan jari -jari sesuai dengan jarak antara pusat dan titik atau sudut gambar.

Kriteria kongruensi sering digunakan karena banyak bagian dan bagian dari semua jenis diproduksi secara seri dan harus memiliki bentuk dan ukuran yang sama. Dengan cara ini mereka dapat dengan mudah diganti jika diperlukan, misalnya mur, sekrup, lembaran atau batu berbatu di jalanan di jalan.

Dapat melayani Anda: aturan Simpson: formula, demonstrasi, contoh, latihanGambar 2. Cobblestones jalanan adalah figur kongruen, karena bentuk dan dimensinya persis sama, meskipun orientasi mereka di lantai dapat berubah. Sumber: Pixabay.

Kesesuaian, identitas dan kesamaan

Ada konsep geometris yang terkait dengan kongruensi, misalnya Angka yang identik dan angka serupa, yang tidak selalu menyiratkan bahwa angka -angka itu kongruen.

Perhatikan bahwa angka -angka kongruen identik, namun segi empat dari Gambar 1 dapat berorientasi dengan cara yang berbeda di pesawat dan masih terus kongruen, karena orientasi yang berbeda tidak mengubah ukuran sisi mereka atau sudut mereka. Dalam hal ini mereka akan berhenti identik.

Konsep lainnya adalah kesamaan angka: dua angka datar serupa jika mereka memiliki bentuk yang sama dan sudut internal mereka mengukur sama, meskipun ukuran angka mungkin berbeda. Jika ini masalahnya, angkanya tidak kongruen.

Contoh Kongruensi

- Kesesuaian sudut

Seperti yang kami sebutkan di awal, sudut yang kongruen memiliki ukuran yang sama. Ada beberapa cara untuk mendapatkan sudut yang kongruen:

Contoh 1

Dua baris dengan titik umum menentukan dua sudut, disebut Sudut yang berlawanan dengan simpul. Sudut -sudut ini memiliki ukuran yang sama, oleh karena itu mereka kongruen.

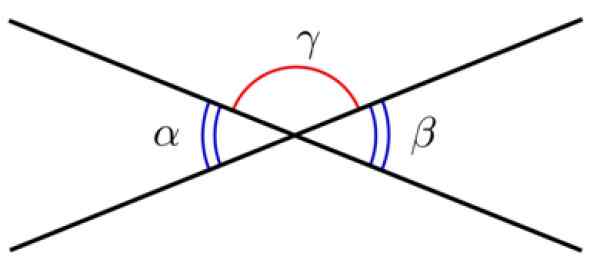Gambar 3. Sudut yang berlawanan dengan simpul. Sumber: Wikimedia Commons.

Contoh 2

Ada dua garis paralel ditambah garis T yang memotong mereka berdua. Seperti pada contoh sebelumnya, ketika garis ini memotong paralelnya menghasilkan sudut kongruen, satu di setiap baris ke sisi kanan dan dua lainnya di sisi kiri. Gambar menunjukkan α dan α₁, Di sebelah kanan garis T, Mereka kongruen.

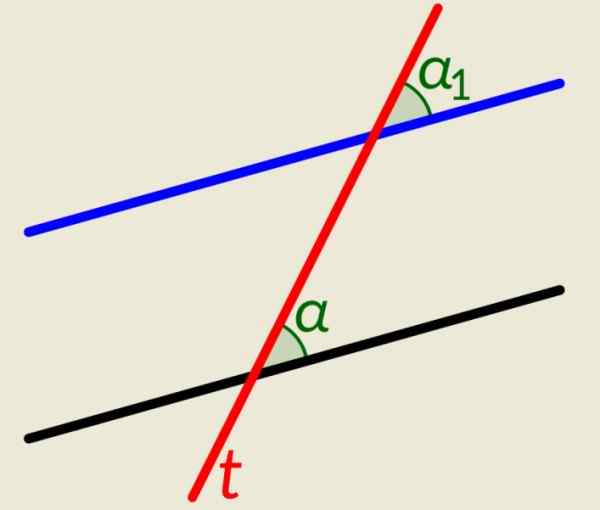Gambar 4. Sudut yang ditunjukkan pada gambar itu kongruen. Sumber: Wikimedia Commons. Lfahlberg/cc by-sa (https: // createveCommons.Org/lisensi/by-sa/3.0).

Contoh 3

Dalam jajaran genjang ada empat sudut internal, yang kongruen dua hingga dua. Mereka adalah orang -orang di antara simpul yang berlawanan, seperti yang ditunjukkan pada gambar berikut, di mana kedua sudut hijau itu kongruen, serta dua sudut berwarna merah.

Dapat melayani Anda: Acutangle Triangle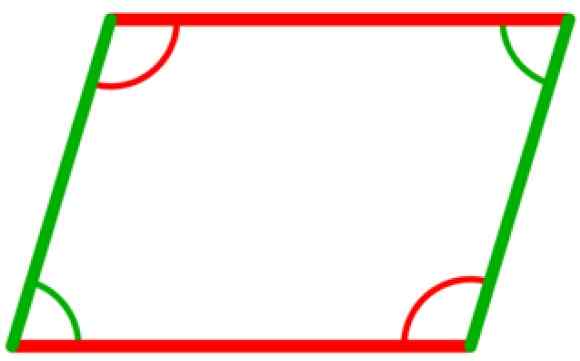Gambar 5. Sudut internal jajaran genjang adalah kongruen dua hingga dua. Sumber: Wikimedia Commons.

- Kongruensi segitiga

Dua segitiga bentuk identik dan ukuran yang sama kongruen. Untuk memverifikasi ini ada tiga kriteria yang dapat diperiksa untuk mencari kongruensi:

-Kriteria LLL: Tiga sisi segitiga memiliki langkah -langkah yang sama, oleh karena itu l₁ = L '₁; L₂ = L '₂ dan saya₃ = L '_3.

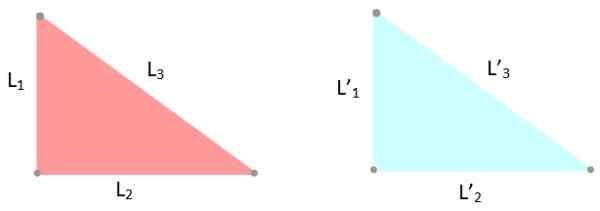Gambar 6. Contoh segitiga kongruen, yang sisinya mengukur hal yang sama. Sumber: f. Zapata.

-Kriteria alla y aal: Segitiga memiliki dua sudut internal yang sama dan sisi antara sudut ini memiliki ukuran yang sama.

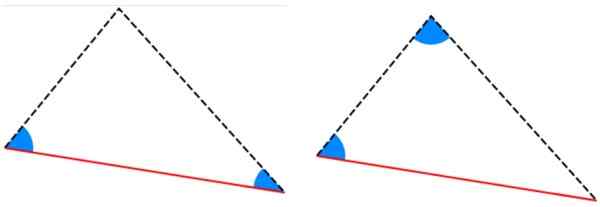Gambar 7. Kriteria ala dan aal untuk kongruensi segitiga. Sumber: Wikimedia Commons.

-Kriteria lal: Dua sisi identik (sesuai) dan di antaranya ada sudut yang sama.

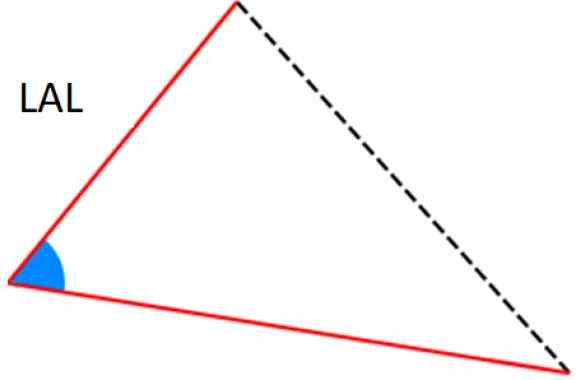Angka 8. Kriteria lal untuk kongruensi segitiga. Sumber: Wikimedia Commons.

Latihan terpecahkan

- Latihan 1

Pada gambar berikut dua segitiga ditunjukkan: ΔABC dan ΔECF. Diketahui bahwa ac = ef, bahwa ab = 6 dan bahwa cf = 10. Selain itu sudut ∡BAC dan ∡FEC adalah kongruen dan sudut ∡ACB dan ∡FCB juga merupakan.

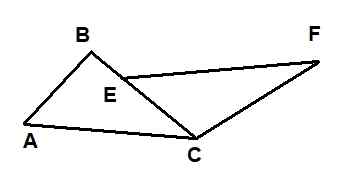Gambar 9. Segitiga untuk contoh diselesaikan 1. Sumber: f. Zapata.

Maka panjang segmen BE sama dengan:

(i) 5 

(Ii) 3

(Iii) 4 

(Iv) 2

(v) 6

Larutan

Karena dua segitiga memiliki satu sisi dengan panjang yang sama AC = EF antara sudut yang sama ∡BAC = ∡CEF dan ∡BCA = ∡Cfe dapat dikatakan bahwa kedua segitiga itu kongruen dengan kriteria sayap.

Yaitu ΔBac ≡ ΔCef, jadi Anda harus:

Ba = Ce = ab = 6

Bc = cf = 10

AC = EF

Tetapi segmen yang ingin Anda hitung adalah menjadi = bc - ec = 10 - 6 = 4.

Sehingga jawaban yang benar adalah (III).

- Latihan 2

Tiga segitiga ditunjukkan pada gambar. Diketahui juga bahwa keduanya menunjukkan sudut masing -masing 80º dan bahwa segmen AB = PD dan AP = CD. Temukan nilai sudut x yang ditunjukkan pada gambar.

Itu dapat melayani Anda: grafik polybal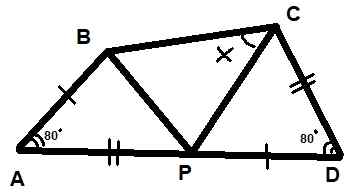Gambar 10. Segitiga untuk contoh diselesaikan 2. Sumber: f. Zapata.

Larutan

Anda harus menerapkan sifat -sifat segitiga, yang dirinci langkah demi langkah.

Langkah 1

Dimulai dengan kriteria untuk kongruensi segitiga lal, dapat dikatakan bahwa segitiga BAP dan PDC kongruen:

ΔBap ≡ ΔPDC

Langkah 2

Di atas mengarah untuk menegaskan bahwa bp = pc, oleh karena itu segitiga ΔBPC adalah sama sekali dan ∡pcb = ∡pbc = x.

Langkah 3

Jika kita menghubungi γ di sudut BPC, itu mengikuti itu:

2x + γ = 180º

Langkah 4

Dan jika kita memanggil β ke sudut APB dan DCP dan α ke sudut ABP dan DPC, itu harus:

α + β + γ = 180º (karena APB adalah sudut datar).

Langkah 5

Selain itu, α + β + 80º = 180º dengan jumlah sudut internal segitiga APB.

Langkah 6

Menggabungkan semua ekspresi yang harus Anda lakukan:

α + β = 100º

Langkah 7

Dan maka dari itu:

γ = 80º.

Langkah 8

Akhirnya itu berarti:

2x + 80º = 180º

Dengan x = 50º.

Referensi

1. Baldor, a. 1973.Geometri datar dan ruang. Budaya Amerika Tengah.
2. Yayasan CK-12. Poligon Kongruen. Diperoleh dari: CK 12.org.
3. Nikmati matematika. Definisi: Radio (Poligon). Pulih dari: nikmatiMaticaticas.com.
4. Referensi Terbuka Matematika. Menguji Poligon untuk Kongruensi. Pulih dari: mathpenref.com.
5. Wikipedia. Kongruensi (geometri). Pulih dari: is.Wikipedia.org.
6. Zapata, f. Segitiga, sejarah, elemen, klasifikasi, properti. Diperoleh dari: Lifer.com.