Properti set terbatas, contoh, latihan diselesaikan

Itu dipahami oleh Set terbatas Semua diatur dengan jumlah elemen terbatas atau akuntansi. Contoh set terbatas adalah kelereng yang terkandung dalam tas, set rumah di lingkungan, atau set P dibentuk oleh dua puluh (20) bilangan alami:

P = 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12,13, 14, 16, 17, 18, 19, 20 

Set bintang alam semesta pasti sangat besar, tetapi tidak diketahui pasti apakah itu terbatas atau tak terbatas. Namun, himpunan planet tata surya terbatas.

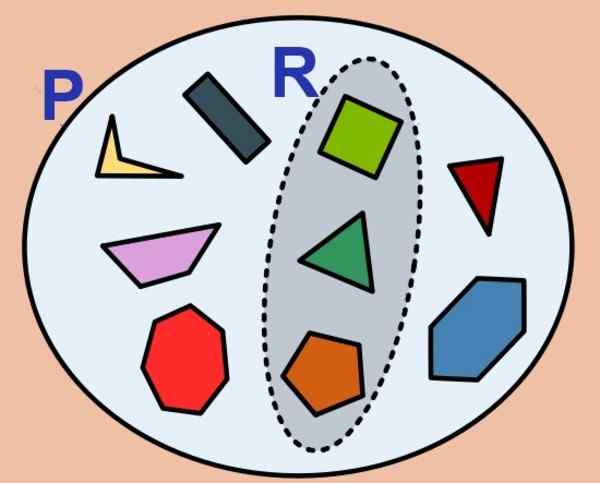
Gambar 1. Himpunan poligon terbatas dan subset dari yang biasa juga. (Wikimedia Commons)

Jumlah elemen set terbatas disebut kardinalitasnya dan untuk set P Itu dilambangkan seperti ini: kartu (P) salah satu #P. Set kosong tidak memiliki kardinalitas dan dianggap sebagai set yang terbatas.

[TOC]

Properti

Di antara sifat set terbatas adalah sebagai berikut:

1- Persatuan Hasil Hasil Hasil Dalam Set Baru.

2- Jika dua set terbatas dicegat, itu adalah set terbatas baru.

3- Subset set terbatas terbatas dan kardinalitasnya kurang dari atau sama dengan set asli.

4- Set kosong adalah set yang terbatas.

Contoh

Ada banyak contoh set terbatas. Di antara beberapa contoh adalah sebagai berikut:

Mengatur M dari bulan -bulan dalam setahun, yang dapat diperpanjang sebagai berikut:

M = Januari, Februari, Maret, April, Mei, Juni, Juli, Agustus, September, Oktober, November, Desember, Kardinalitas M adalah 12.

Mengatur S hari -hari dalam seminggu: S = Senin, Selasa, Rabu, Kamis, Jumat, Sabtu, Minggu. Kardinalitas S adalah 7.

Dapat melayani Anda: Hubungan Proporsionalitas: Konsep, Contoh dan Latihan

Mengatur N Dari huruf -huruf alfabet Spanyol itu adalah set yang terbatas, set ini dengan ekstensi ditulis seperti ini:

N = A, b, c, d, e, f, g, h, i, j, k, l, m, n, ñ, o, p, q, r, s, t, u, v, w, w, W, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, W, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, w, x, y, z dan itu Kardinalitas adalah 27.

Mengatur V Dari vokal dalam bahasa Spanyol itu adalah subset dari set:

V ⊂ N Oleh karena itu adalah set yang terbatas.

Set terbatas V Cara diperpanjang ditulis seperti ini: V = a, e, i, o, u dan kardinalitasnya 5.

Set dapat diungkapkan dengan pemahaman. Mengatur F Terdiri dari huruf kata "terbatas" adalah contoh:

F = x / x adalah huruf kata "terbatas"

Set ini diekspresikan secara luas adalah:

F = f, i, n, t, o yang kardinalitasnya 5 dan oleh karena itu adalah set yang terbatas.

Lebih banyak contoh

Warna pelangi adalah contoh himpunan terbatas lainnya, set C dari warna -warna ini adalah:

C = merah, oranye, kuning, hijau, cyan, biru, violet dan kardinalitasnya adalah 7.

Set fase F Dari bulan adalah contoh lain yang terbatas:

F = Bulan Baru, Kamar Tumbuh, Bulan Purnama, Kamar Waning Set ini memiliki kardinalitas 4.

Gambar 2. Planet -planet tata surya membentuk set yang terbatas. (Pixabay)

Set terbatas lainnya adalah yang dibentuk oleh planet -planet tata surya:

P = Merkurius, Venus, Bumi, Mars, Jupiter, Saturnus, Uranus, Neptunus, Pluto Cardinality 9.

Latihan terpecahkan

Latihan 1

Set berikut diberikan a = x∊ r / x^3 = 27. Ekspresikan dengan kata -kata dan tulis dengan ekstensi, tunjukkan kardinalitasnya dan katakan apakah itu terbatas atau tidak.

Dapat melayani Anda: elips

Larutan: Set A adalah himpunan bilangan real x sedemikian rupa sehingga X diangkat ke kubus sebagai hasilnya 27.

Persamaan x^3 = 27 memiliki tiga solusi: yaitu x1 = 3, x2 = (-3/2 + 3√3/2 i) dan x3 = (-3/2-3√3/2 i). Dari tiga solusi hanya X1 yang nyata, sedangkan dua lainnya adalah bilangan kompleks.

Karena definisi set A mengatakan bahwa x milik bilangan real, maka solusi dalam bilangan kompleks bukan bagian dari set.

Set yang diperluas adalah:

A = 3, yang merupakan set kardinalitas 1 yang terbatas.

Latihan 2

Tulis secara simbolis (dengan pemahaman) dan secara luas himpunan b bilangan real yang lebih besar dari 0 (nol) dan lebih sedikit atau sama dari 0 (nol). Tunjukkan kardinalitas Anda dan apakah itu terbatas atau tidak.

Larutan: B = x∊ r / 0 < x <= 0

Set B kosong karena bilangan real x tidak dapat secara bersamaan lebih besar dan kurang dari nol, serta 0 dan juga kurang dari 0.

B = dan kardinalitasnya adalah 0. Set kosong adalah set yang terbatas.

Latihan 3

Set solusi dari persamaan tertentu diberikan. Set dengan pemahaman ditulis seperti ini:

S = x∊ r / (x -3) (x^2 - 9x + 20) = 0

Tuliskan set ini secara luas, tunjukkan kardinalitas Anda dan tunjukkan apakah itu set yang terbatas atau tidak.

Larutan: Pertama, dengan menganalisis ekspresi yang menggambarkan himpunan S, diperoleh bahwa itu adalah satu set nilai x nyata yang merupakan solusi dari persamaan:

(x -3) (x^2 - 9x + 20) = 0 (*)

Solusi dari persamaan ini adalah x = 3, yang merupakan bilangan real dan karenanya milik S. Tetapi ada lebih banyak solusi yang dapat diperoleh mencari solusi dari persamaan kuadrat:

Dapat melayani Anda: distribusi f: karakteristik dan latihan diselesaikan

(x^2 - 9x + 20) = 0

Ekspresi sebelumnya dapat menjadi faktor sebagai berikut:

(x - 4) (x - 5) = 0

Yang membawa kita ke dua solusi lagi dari persamaan asli (*) yaitu x = 4 dan x = 5. Singkatnya, Persamaan (*) memiliki solusi 3, 4 dan 5.

Set S yang diekspresikan secara luas adalah seperti ini:

S = 3, 4, 5, yang memiliki kardinalitas 3 dan karenanya merupakan set yang terbatas.

Latihan 4

Ada dua set a = 1, 5, 7, 9, 11 dan b = x ∊ n / x adalah par ^ x x < 10 .

Secara eksplisit menulis set B dan temukan serikat pekerja dengan himpunan a. Temukan juga intersepsi kedua set ini dan simpulkan.

Larutan: Set B terdiri dari bilangan alami sedemikian rupa sehingga mereka bahkan dan juga lebih rendah dari nilai 10, oleh karena itu bersama B secara luas ditulis sebagai berikut:

B = 2, 4, 6, 8

Persatuan Set A dengan Set B adalah:

A U B = 1, 2, 4, 5, 6, 7, 8, 9, 11

dan intersepsi set A dengan set B ditulis seperti ini:

A ⋂ b = = Ø adalah set kosong. 

Perlu dicatat bahwa persatuan dan intersepsi dari dua set terbatas ini mengarah ke set baru, yang pada gilirannya juga terbatas.

Referensi

1. Sumber, a. (2016). Matematika Dasar. Pengantar Perhitungan. Lulu.com.
2. Garo, m. (2014). Matematika: Persamaan Kuadrat: Bagaimana Memecahkan Persamaan Kuadratik. Marilù Garo.
3. Haeussler, e. F., & Paul, R. S. (2003). Matematika untuk Administrasi dan Ekonomi. Pendidikan Pearson.
4. Jiménez, J., Rodríguez, m., Estrada, r. (2005). Matematika 1 Sep. Ambang.
5. Berharga, c. T. (2005). Kursus Matematika 3o. Progreso editorial.
6. Matematika 10 (2018). "Contoh set terbatas". Diperoleh dari: Mathematics10.bersih
7. Rock, n. M. (2006). Aljabar saya mudah! Begitu mudah. Team Rock Press.
8. Sullivan, J. (2006). Aljabar dan Trigonometri. Pendidikan Pearson.
9. Wikipedia. Set terbatas. Pulih dari: is.Wikipedia.com