Integrasi makna konstan, perhitungan dan contoh

Itu Integrasi Konstan Ini adalah nilai tambah untuk perhitungan antiderivatif atau integral, berfungsi untuk mewakili solusi yang membentuk primitif dari suatu fungsi. Mengekspresikan ambiguitas yang melekat di mana fungsi apa pun memiliki jumlah primitif yang tak terbatas.

Misalnya jika fungsi diambil: f (x) = 2x + 1 dan kami mendapatkan antiderivatifnya:

∫ (2x+1) dx = x² + X + C ; Di mana C Ini adalah Integrasi Konstan dan secara grafis mewakili terjemahan vertikal antara kemungkinan yang tak terbatas dari primitif. Benar untuk mengatakan itu (x² + x) Itu A dari f primitif (x).

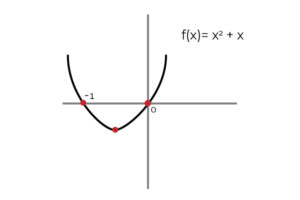Sumber: Penulis

Dengan cara yang sama Anda dapat mendefinisikan (x² + X + C ) sebagai primitif f (x).

[TOC]

Properti terbalik

Dapat dicatat bahwa ketika diturunkan ekspresi (x² + x) fungsi f (x) = 2x + 1 diperoleh. Ini karena sifat terbalik antara derivasi dan integrasi fungsi. Properti ini memungkinkan untuk mendapatkan rumus integrasi mulai dari diferensiasi. Yang memungkinkan verifikasi integral melalui turunan yang sama.

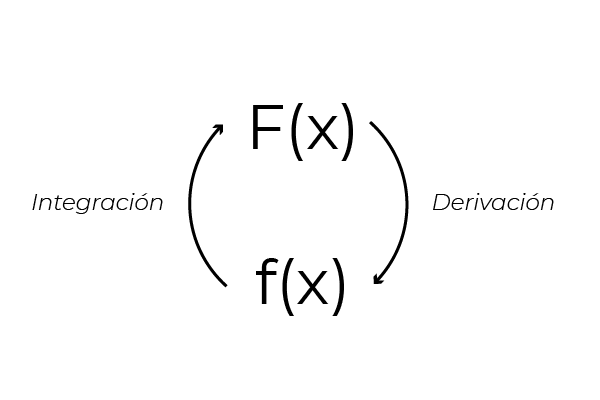Sumber: Penulis

Namun (x² + x) Ini bukan satu -satunya fungsi yang turunannya sama dengan (2x + 1).

1. D (X² + x)/ dx = 2x + 1
2. D (X² + x + 1)/ dx = 2x + 1
3. D (X² + x + 2)/ dx = 2x + 1
4. D (X² + x + 3)/ dx = 2x + 1
5. D (X² + X + C)/ dx = 2x + 1

Di mana 1, 2, 3 dan 4 mewakili primitif tertentu dari f (x) = 2x + 1. Sedangkan 5 mewakili integral atau primitif f (x) = 2x + 1.

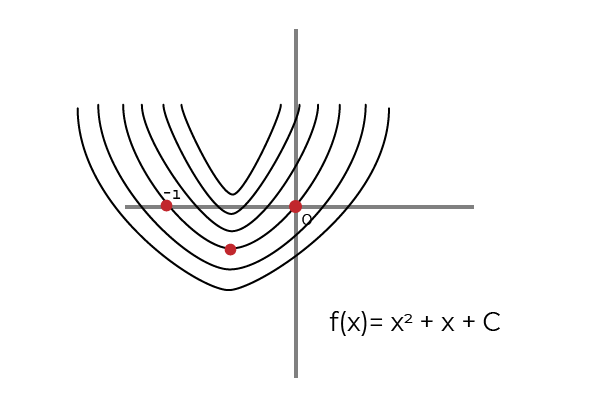Sumber: Penulis

Primitif suatu fungsi dicapai melalui antidivasi atau proses integral. Di mana f akan menjadi f primitif jika berikut ini terpenuhi

• y = ∫ f (x) dx = F (x) + c; C = Integrasi Konstan
• F '(x) = f (x)

Dihargai bahwa suatu fungsi memiliki turunan tunggal, tidak seperti primitifnya yang tak terbatas yang dihasilkan dari integrasi.

Integral yang tidak terbatas

 ∫ f (x) dx = f (x) + c

Ini sesuai dengan keluarga kurva dengan pola yang sama, yang mengalami ketidaksesuaian dalam nilai gambar setiap titik (x, y). Setiap fungsi yang memenuhi pola ini akan menjadi primitif individu dan himpunan semua fungsi dikenal sebagai Integral yang tidak terbatas.

Nilai dari Integrasi Konstan Itu akan menjadi salah satu yang membedakan setiap fungsi dalam praktik.

Itu Integrasi Konstan Ini menunjukkan perpindahan vertikal di semua grafik yang mewakili primitif dari suatu fungsi. Di mana paralelisme diamati di antara mereka, dan fakta itu C Itu adalah nilai perpindahan.

Menurut Praktik Umum Integrasi Konstan Itu dilambangkan dengan huruf "C" setelah penambahan, meskipun dalam praktiknya itu acuh tak acuh jika konstanta menambah atau mengurangi. Nilai sebenarnya dapat ditemukan dengan berbagai cara menurut berbeda kondisi awal.

Makna lain dari konstanta integrasi

Sudah ada pembicaraan tentang bagaimana Integrasi Konstan diterapkan di cabang Kalkulus integral; Mewakili keluarga kurva yang mendefinisikan integral yang tidak terbatas. Tetapi banyak ilmu dan cabang lainnya telah menetapkan nilai -nilai yang sangat menarik dan praktis dari Integrasi Konstan, yang telah memfasilitasi pengembangan beberapa studi.

Dapat melayani Anda: trapesium persegi panjang: sifat, hubungan dan formula, contoh

Dalam fisik Konstanta integrasi dapat mengambil beberapa nilai sesuai dengan sifat data. Contoh yang sangat umum adalah mengetahui fungsinya V (t) yang mewakili kecepatan dari sebuah partikel versus waktu t. Diketahui bahwa saat menghitung v (t) primitif fungsi diperoleh R (t) yang mewakili posisi dari partikel versus waktu.

Itu Integrasi Konstan akan mewakili nilai posisi awal, yaitu pada saat ini t = 0.

Demikian pula, jika fungsinya diketahui PADA)  yang mewakili percepatan dari partikel versus waktu. Primitif a (t) akan menghasilkan fungsi v (t), di mana Integrasi Konstan Itu akan menjadi nilai kecepatan awal v₀.

Dalam ekonomi, dengan memperoleh primitif fungsi biaya dengan integrasi. Itu Integrasi Konstan akan mewakili biaya tetap. Dan begitu banyak aplikasi lain yang pantas diferensial dan integral kalkulus.

Bagaimana integrasi konstan dihitung?

Untuk perhitungan Integrasi Konstan, Akan selalu perlu mengetahui kondisi awal. Yang bertanggung jawab untuk mendefinisikan primitif mana yang mungkin sesuai.

Dalam banyak aplikasi ini diperlakukan sebagai variabel independen untuk waktu (t), di mana konstanta C mengambil nilai yang menentukan kondisi awal dari kasus tertentu.

Jika contoh awal diambil: ∫ (2x+1) dx = x² + X + C

Kondisi awal yang valid dapat untuk mengkondisikan grafik untuk melewati koordinat tertentu. Misalnya, diketahui bahwa primitif (x² + X + C) Pergi melalui titik (1, 2)

F (x) = x² + X + C; Ini adalah solusi umum

F (1) = 2

Kami mengganti solusi umum dalam kesetaraan ini

F (1) = (1)² + (1) + C = 2

Di mana mudah disimpulkan C = 0

Dengan cara ini primitif yang sesuai untuk kasus ini adalah F (x) = x² + X

Ada berbagai jenis latihan numerik yang bekerja dengannya Konstanta Integrasi. Faktanya, kalkulus diferensial dan integral tidak berhenti diterapkan dalam investigasi saat ini. Di berbagai tingkat akademik yang dapat Anda temukan; Dari perhitungan awal, melalui fisika, kimia, biologi, ekonomi, antara lain.

Itu juga dihargai dalam studi Persamaan diferensial, Dimana Integrasi Konstan Anda dapat mengambil berbagai nilai dan solusi, ini karena beberapa rujukan dan integrasi yang dilakukan dalam hal ini.

Contoh

Contoh 1

1. Sebuah meriam yang terletak 30 meter tinggi tunas secara vertikal ke atas proyektil. Diketahui bahwa kecepatan proyektil awal adalah 25 m/s. Menentukan:

• Fungsi yang mendefinisikan posisi proyektil sehubungan dengan waktu.
• Waktu penerbangan atau waktu di mana partikel memainkan tanah.

Itu dapat melayani Anda: 8 jenis kesalahan pengukuran (dengan contoh)

Diketahui bahwa dalam akselerasi gerakan bujursangkar yang bervariasi secara seragam adalah nilai konstan. Ini adalah kasus peluncuran proyektil, di mana akselerasi akan menjadi gravitasi

G = - 10 m/s²

Diketahui juga bahwa akselerasi adalah yang kedua yang berasal dari posisi, menunjukkan integrasi ganda ke dalam resolusi latihan, sehingga mendapatkan dua Konstanta Integrasi.

A (t) = -10

V (t) = ∫a (t) dt = ∫ (-10t) dt = -10t + C₁

Kondisi awal latihan menunjukkan bahwa kecepatan awal adalah v₀ = 25 m/s. Ini adalah kecepatan pada saat waktu t = 0. Dengan cara ini terpenuhi bahwa:

V (0) = 25 = -10 (0) + C₁   Dan C₁ = 25

Fungsi kecepatan didefinisikan

V (t) = -10t + 25; Anda dapat melihat kesamaan dengan formula mRUV (v_F = V₀ + A x t)

Dalam homolog, fungsi kecepatan terintegrasi untuk mencapai ekspresi yang mendefinisikan posisi:

R (t) = ∫V (t) dt = ∫ (-10t+25) dt = -5t² + 25t + C₂

R (t) = -5t² + 25t + C₂  (Posisi primitif)

Posisi awal r (0) = 30 m diketahui. Maka primitif khusus dari proyektil dihitung.

R (0) = 30m = -5 (0)² + 25 (0) + C₂ . Di mana C₂ = 30

Bagian pertama diselesaikan sejak itu R (t) = -5t² + 25t + 30  ; Ekspresi ini homolog dari rumus perpindahan dalam mruv r (t) = r₀ + V₀T - gt²/2

Untuk bagian kedua persamaan kuadratik harus diselesaikan: -5t² + 25t + 30 = 0

Karena kondisi partikel untuk mencapai tanah (posisi = 0)

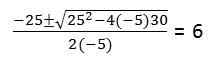Sumber: Penulis

Sebenarnya persamaan kelas 2 melempar 2 solusi t: 6, -1. Nilai t = -1 diabaikan karena ini adalah satuan waktu yang domainnya tidak termasuk angka negatif.

Dengan cara ini bagian kedua di mana waktu penerbangan sama dengan 6 detik diselesaikan.

Contoh 2

2. Temukan f (x) primitif yang memenuhi kondisi awal:

• f "(x) = 4; f '(2) = 2; f (0) = 7

Dengan informasi dari turunan kedua F "(x) = 4 Proses antidivasi dimulai

f '(x) = ∫f "(x) dx

∫4 dx = 4x + c₁

Kemudian, mengetahui kondisi f '(2) = 2 hasil:

4 (2) + C₁ = 2

C₁ = -6 dan f '(x) = 4x - 8

Lanjutkan dengan cara yang sama untuk yang kedua Integrasi Konstan

f (x) = ∫f '(x) dx
∫ (4x - 8) dx = 2x² - 8x + c₂

Kondisi awal f (0) = 7 diketahui dan lanjutkan:

2 (0)² - 8 (0) + C₂ = 7

C₂ = 7 dan f (x) = 2x² - 8x + 7

• f "(x) = x² ; f '(0) = 6; f (0) = 3

Mirip dengan masalah sebelumnya kami mendefinisikan turunan pertama dan fungsi asli dari kondisi awal.

f '(x) = ∫f "(x) dx

∫ (x²) Dx = (x³/3) + C₁

Dengan kondisi f '(0) = 6 hasil:

Dapat melayani Anda: Teori Set: Karakteristik, Elemen, Contoh, Latihan

(0³/3) + C₁ = 6; Di mana₁ = 6 dan f '(x) = (x³/3) + 6

Lalu yang kedua Integrasi Konstan

f (x) = ∫f '(x) dx

∫ [(x³/3) + 6] dx = (x⁴/12) + 6x + c₂

Kondisi awal f (0) = 3 diketahui dan lanjutkan:

[(0)⁴/12] + 6 (0) + C₂ = 3; Di mana₂ = 3

Primitif tertentu diperoleh

f (x) = (X⁴/12) + 6x + 3

Contoh 3

3. Tentukan fungsi primitif yang diberikan turunan dan titik grafik:

• dy/dx = 2x - 2 yang melewati titik (3, 2)

Penting untuk diingat bahwa turunannya merujuk pada kemiringan garis garis singgung ke kurva pada titik tertentu. Di mana tidak benar untuk mengasumsikan bahwa grafik turunannya menyentuh titik yang ditunjukkan, karena itu milik grafik fungsi primitif.

Dengan cara ini kami mengekspresikan persamaan diferensial sebagai berikut:

dy = (2x - 2) DX  ; Kemudian saat menerapkan kriteria antidivasi yang Anda miliki:

∫dy = ∫ (2x - 2) dx

y = x² - 2x + c

Menerapkan kondisi awal:

2 = (3)² - 2 (3) + C

C = -1

Diperoleh: f (x) = x² - 2x - 1

• dy/dx = 3x² - 1 yang melewati titik (0, 2)

Kami mengekspresikan persamaan diferensial sebagai berikut:

dy = (3x² - 1) DX  ; Kemudian saat menerapkan kriteria antidivasi yang Anda miliki:

 ∫dy = ∫ (3x² - 1) DX

y = x³ - x + c

Menerapkan kondisi awal:

2 = (0)² - 2 (0) + C

C = 2

Diperoleh: f (x) = x³ - x + 2

Latihan yang diusulkan

Latihan 1

1. Temukan f (x) primitif yang memenuhi kondisi awal:

• f "(x) = x; f '(3) = 1; f (2) = 5
• f "(x) = x + 1; f '(2) = 2; f (0) = 1
• f "(x) = 1; f '(2) = 3; f (1) = 10
• f "(x) = -x; f '(5) = 1; f (1) = -8

Latihan 2

2. Balon yang naik dengan kecepatan 16 kaki/s melepaskan jaket pasir dari ketinggian 64 kaki di atas permukaan tanah.

• Tentukan waktu penerbangan
• Apa yang akan menjadi vektor v_F Saat Anda menyentuh lantai?

Latihan 3

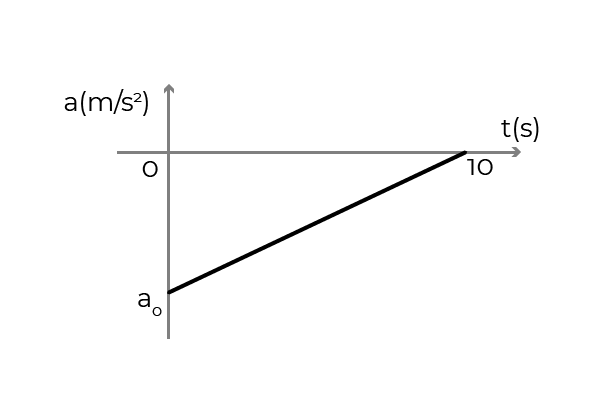
3. Gambar tersebut menunjukkan grafik akselerasi - waktu mobil yang bergerak dalam arti positif sumbu x. Mobil itu bepergian ke kecepatan konstan 54 km/jam ketika pengemudi menerapkan rem untuk berhenti dalam 10 detik. Menentukan:

• Percepatan awal mobil
• Kecepatan mobil pada t = 5s
• Perpindahan mobil selama pengereman

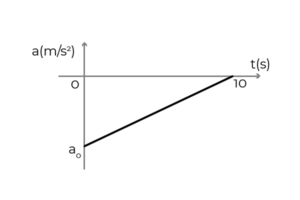Sumber: Penulis

Latihan 4

4. Tentukan fungsi primitif yang diberikan turunan dan titik grafik:

• dy/dx = x yang melewati titik (-1, 4)
• dy/dx = -x² + 1 yang melewati titik (0, 0)
• dy/dx = -x + 1 yang melewati titik (-2, 2)

Referensi

1. Kalkulus integral. Metode integral dan integrasi yang tidak ditentukan. Wilson, Velásquez Bastidas. Universitas Magdalena 2014
2. Stewart, J. (2001). Perhitungan variabel. Transenden awal. Meksiko: Thomson Learning.
3. Jiménez, r. (2011). Matematika VI. Kalkulus integral. Meksiko: Pendidikan Pearson.
4. Fisika i. MC Graw Hill