Proporsionalitas konstan apa itu, perhitungan, latihan

Itu Proporsionalitas konstan Ini adalah elemen numerik relasional, yang digunakan untuk menentukan pola kesamaan antara 2 besaran yang secara bersamaan diubah. Sangat umum untuk mewakili itu sebagai fungsi linier generik melalui ekspresi f (x) = k.X. Namun, ini bukan satu -satunya representasi dari kemungkinan proporsionalitas.

Sebagai contoh, hubungan antara x dan y dalam fungsi y = 3x memiliki konstanta proporsionalitas sama dengan 3. Ini menunjukkan bahwa ketika variabel independen X tumbuh, begitu pula variabel dependen dan, dalam tiga kali lipat dari nilai sebelumnya.

Perubahan yang diterapkan dalam satu variabel, memiliki dampak langsung di sisi lain, sehingga ada nilai yang dikenal sebagai konstan proporsionalitas. Ini berfungsi untuk menghubungkan berbagai magnitudo yang diperoleh kedua variabel.

[TOC]

Apa konstanta proporsionalitas dan tipe

Menurut tren dalam mengubah variabel, proporsionalitas dapat diklasifikasikan menjadi 2 jenis.

Proporsionalitas langsung

Menyarankan hubungan searah antara dua besaran. Di dalamnya, jika variabel independen menyajikan beberapa pertumbuhan, variabel dependen juga akan tumbuh. Demikian pula, setiap penurunan variabel independen akan menyebabkan penurunan besarnya dan.

Misalnya, fungsi linier yang digunakan dalam pengantar; Y = 3x, sesuai dengan rasio langsung proporsionalitas. Ini karena peningkatan variabel independen x akan menyebabkan peningkatan tiga dalam nilai sebelumnya yang diambil oleh variabel dependen dan.

Demikian pula, variabel dependen akan mengurangi triple nilainya ketika x turun dalam besarnya.

Nilai konstanta proporsionalitas "k" dalam hubungan langsung didefinisikan sebagai k = y/x.

Proporsionalitas terbalik atau tidak langsung

Dalam jenis fungsi ini, hubungan antara variabel disajikan dengan cara antonim, di mana pertumbuhan atau penurunan variabel independen masing -masing sesuai dengan penurunan atau pertumbuhan variabel dependen.

Itu dapat melayani Anda: dekomposisi bilangan alami (contoh dan latihan)

Misalnya, fungsi f (x) = k/x adalah hubungan terbalik atau tidak langsung. Karena nilai variabel independen mulai meningkat, nilai k akan dibagi dengan angka yang tumbuh, membuat variabel dependen berkurangnya nilai sesuai dengan proporsinya.

Menurut nilai yang diambil oleh K, kecenderungan fungsi terbalik proporsional dapat ditentukan. Jika k> 0, maka fungsinya akan berkurang di semua bilangan real. Dan grafiknya akan berlokasi di kuadran 1 dan ke -3.

Sebaliknya, jika nilai k negatif atau kurang dari nol, fungsinya akan meningkat dan grafiknya akan ditemukan di kuadran ke -2 dan 4.

Bagaimana itu dihitung?

Ada konteks yang berbeda di mana definisi konstanta proporsionalitas mungkin diperlukan. Dalam kasus yang berbeda, data yang berbeda tentang masalah akan ditampilkan, di mana studi ini akhirnya akan menunjukkan nilai k.

Dengan cara generik, yang disebutkan di atas dapat direkapitulasi. Nilai k sesuai dengan dua ekspresi sesuai dengan jenis proporsionalitas yang ada:

- Langsung: k = y/x

- Terbalik atau tidak langsung: k = y.X

Menurut grafik Anda

Terkadang hanya grafik fungsi yang akan diketahui sebagian atau sepenuhnya. Dalam kasus ini perlu, dengan analisis grafik, tentukan jenis proporsionalitas. Maka kita harus mendefinisikan koordinat yang memungkinkan untuk memverifikasi nilai x dan y untuk diterapkan pada rumus k yang sesuai.

Grafik yang mengacu pada proporsionalitas langsung adalah tipe linier. Di sisi lain, grafik fungsi proporsional terbalik biasanya berbentuk hiperbolas.

Menurut Tabel Nilai

Dalam beberapa kasus ada tabel nilai dengan nilai yang sesuai dengan setiap iterasi dari variabel independen. Biasanya ini menyiratkan realisasi grafik selain mendefinisikan nilai k.

Dapat melayani Anda: distribusi frekuensi: cara membuat tabel, contoh, olahraga

Menurut ekspresi analitik

Menunjukkan ekspresi yang mendefinisikan secara analitik. Secara langsung nilai k bisa jelas, atau juga dapat disimpulkan dari ekspresi itu sendiri.

Sebagai aturan tiga langsung atau majemuk

Dalam model latihan lain ada data tertentu, yang merujuk pada hubungan antara nilai -nilai. Ini membuat penerapan tiga langsung atau senyawa untuk mendefinisikan data lain yang diperlukan di tahun ini.

Sejarah

Konsep proporsionalitas selalu ada. Tidak hanya dalam pikiran dan pekerjaan matematikawan yang hebat, tetapi dalam kehidupan sehari -hari populasi, karena kepraktisan dan penerapannya.

Sangat umum untuk memenuhi situasi yang membutuhkan pendekatan proporsionalitas. Ini disajikan dalam setiap kasus di mana variabel dan fenomena dibandingkan yang menjaga hubungan tertentu.

Melalui garis waktu kita dapat mengkarakterisasi momen historis, di mana kemajuan matematika mengenai proporsionalitas telah diterapkan.

- Abad kedua a.C. Sistem penyimpanan fraksi dan proporsi di Yunani diadopsi.

- Abad ke -5 a.C. Proporsi yang menghubungkan sisi dan diagonal persegi juga ditemukan di Yunani.

- 600 a.C. Tales de Mileto menyajikan teorema tentang proporsionalitas.

- Tahun 900. Sistem desimal yang sebelumnya digunakan oleh India dalam alasan dan proporsi diperpanjang. Kontribusi yang dibuat oleh orang Arab.

- XVII Century. Kontribusi merujuk pada proporsi dalam perhitungan Euler tiba.

- XIX Century. Gauss memberikan konsep bilangan dan proporsi yang kompleks.

- Abad ke dua puluh. Proporsionalitas sebagai model fungsi ditentukan oleh gula dan deulofeo.

Latihan terpecahkan

Latihan 1

Diperlukan untuk menghitung nilai variabel x, y, z dan g. Mengetahui hubungan proporsional berikut:

3x + 2y - 6z + 8g = 1925

Dapat melayani Anda: variabel acak kontinu

x/3 = y/8 = z/3 = g/5

Nilai relatif dari konstanta proporsionalitas didefinisikan. Ini dapat diperoleh dari hubungan kedua, di mana nilai yang membagi setiap variabel menunjukkan hubungan atau alasan mengenai k.

X = 3k y = 2k z = 3k g = 5k

Nilai diganti dalam ekspresi pertama, di mana sistem baru akan dievaluasi dalam variabel k tunggal.

3 (3k) + 2 (2k) - 6 (3k) + 8 (5k) = 1925

9K + 4K -18K + 40K = 1925

35k = 1925

K = 1925/35 = 55

Menggunakan nilai konstanta proporsionalitas ini kita dapat menemukan gambar yang mendefinisikan masing -masing variabel.

x = 3 (55) = 165 y = 2 (55) = 110

Z = 3 (55) = 165 g = 5 (55) = 275

Latihan 2

Hitung konstanta proporsionalitas dan ekspresi yang mendefinisikan fungsi, mengingat grafiknya.

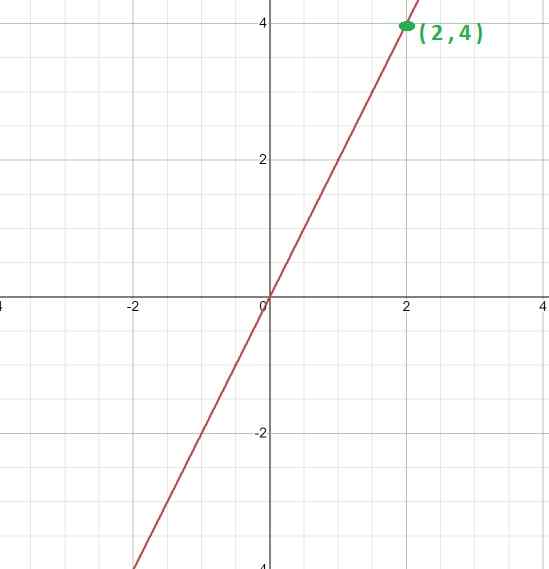
Pertama, grafik dianalisis, karakter liniernya terbukti. Ini menunjukkan bahwa itu adalah fungsi dengan proporsionalitas langsung dan bahwa nilai k akan diperoleh melalui ekspresi k = y/x

Kemudian titik yang dapat ditentukan dari grafik dipilih, yaitu, di mana koordinat yang menyusunnya bisa tepat.

Untuk kasus ini, intinya diambil (2, 4). Di mana kita dapat membangun hubungan berikut.

K = 4/2 = 2

Sehingga ekspresi didefinisikan oleh fungsi y = kx, yang untuk kasus ini akan

F (x) = 2x

Referensi

1. Matematika untuk Listrik & Elektronik. Kata. Arthur Kramer. Pembelajaran Cengage, 27 Jul. 2012
2. Visi 2020: Peran strategis penelitian operasional. N. Ravichandran. Penerbit Allied, 11 September. 2005
3. Pengetahuan Gramatikal dan Aritmatika dari Asisten Administrasi Negara.e-book. Mad-eduform
4. Penguatan Matematika untuk Dukungan dan Diversifikasi Kurikuler: Untuk Dukungan dan Diversifikasi Kurikuler. Mª Lourdes Lázaro Soto. Narcea Ediciones, 29 Agustus. 2003
5. Logistik dan Manajemen Komersial. Maria José Escudero Serrano. Edisi paraninfo, s.KE., 1 September. 2013