Berapa banyak solusi yang dimiliki persamaan kuadratik?

Persamaan kuadratik atau persamaan tingkat kedua dapat memiliki nol, satu atau dua solusi nyata, tergantung pada koefisien yang muncul dalam persamaan tersebut. Jika Anda mengerjakan bilangan kompleks, maka Anda dapat mengatakan bahwa setiap persamaan kuadratik memiliki dua solusi.

Untuk memulai persamaan kuadratik, ini adalah persamaan dari bentuk ax²+bx+c = 0, di mana a, b dan c adalah bilangan real dan x adalah variabel.

Dikatakan bahwa X1 adalah solusi dari persamaan kuadratik sebelumnya jika ketika mengganti x oleh x1 persamaannya terpenuhi, yaitu, jika a (x1) ²+b (x1)+c = 0.

Jika Anda memiliki misalnya persamaan x²-4x+4 = 0, maka x1 = 2 adalah solusinya, karena (2) ² (2) +4 = 4-8+4 = 0.

Sebaliknya, jika x2 = 0 diganti, diperoleh (0) ²-4 (0) +4 = 4 dan sebagai 4 ≠ 0 lalu x2 = 0 bukan solusi dari persamaan kuadratik.

Solusi dari persamaan kuadratik

Jumlah solusi dari persamaan kuadratik dapat dipisahkan dalam dua kasus yang adalah:

1.- Dalam bilangan real

Saat bekerja dengan bilangan real, persamaan kuadratik dapat memiliki:

-Solusi Nol: Artinya, tidak ada bilangan real yang memenuhi persamaan kuadratik. Sebagai contoh, persamaan yang diberikan x²+1 = 0, tidak ada bilangan real sehingga memenuhi persamaan tersebut, karena kedua x² lebih besar dari atau sama dengan nol dan 1 lebih ketat dari nol, sehingga jumlahnya akan lebih besar akan lebih besar akan menjadi lebih besar Ketat dari nol.

-Solusi berulang: Ada satu nilai nyata yang memenuhi persamaan kuadratik. Misalnya, satu-satunya solusi persamaan x²-4x+4 = 0 adalah x1 = 2.

-Dua solusi berbeda: Ada dua nilai yang memenuhi persamaan kuadratik. Misalnya, x²+x -2 = 0 memiliki dua solusi berbeda yaitu x1 = 1 dan x2 = -2.

2.- Dalam bilangan kompleks

Saat bekerja dengan bilangan kompleks, persamaan kuadrat selalu memiliki dua solusi, yaitu Z1 dan Z2 di mana Z2 adalah konjugat Z1. Selain itu, mereka dapat diklasifikasikan sebagai:

-Kompleks: Solusi dari bentuk z = p ± qi, di mana p dan q adalah bilangan real. Kasing ini sesuai dengan kasus pertama dari daftar sebelumnya.

-Kompleks murni: Itu adalah ketika bagian nyata dari solusi sama dengan nol, yaitu bahwa solusi memiliki bentuk z = ± qi, di mana q adalah bilangan real. Kasing ini sesuai dengan kasus pertama dari daftar sebelumnya.

-Kompleks dengan bagian imajiner sama dengan nol: Itu adalah ketika bagian kompleks dari solusi sama dengan nol, yaitu bahwa solusinya adalah bilangan real. Kasing ini sesuai dengan dua kasus terakhir dari daftar sebelumnya.

Bagaimana solusi dari persamaan kuadrat yang dihitung?

Untuk menghitung solusi dari persamaan kuadratik, rumus yang dikenal sebagai "resolusi" digunakan, yang mengatakan bahwa solusi persamaan AX²+BX+C = 0 diberikan dengan ekspresi gambar berikut:

Jumlah yang muncul di dalam akar kuadrat disebut diskriminan persamaan kuadratik dan dilambangkan dengan huruf "D".

Persamaan kuadrat akan memiliki:

-Dua solusi nyata ya, dan hanya ya, d> 0.

-Solusi nyata berulang jika, dan hanya jika, d = 0.

-Nol solusi nyata (atau dua solusi kompleks) ya, dan hanya ya, D<0.

Contoh

-Solusi persamaan x²+x-2 = 0 diberikan oleh:

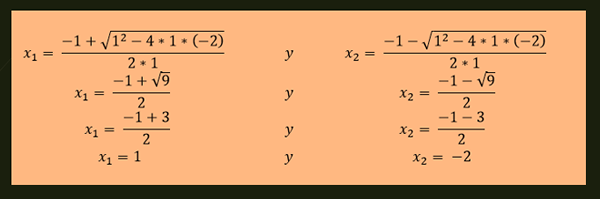
-Persamaan X²-4X+4 = 0 memiliki solusi berulang yang diberikan oleh:

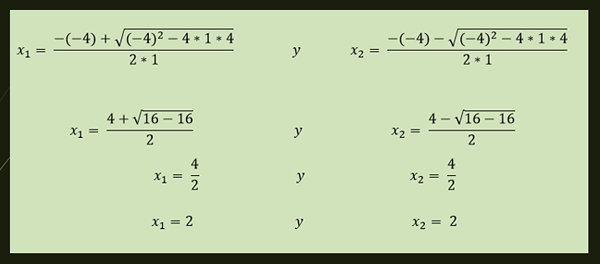
-Solusi persamaan x²+1 = 0 diberikan oleh:

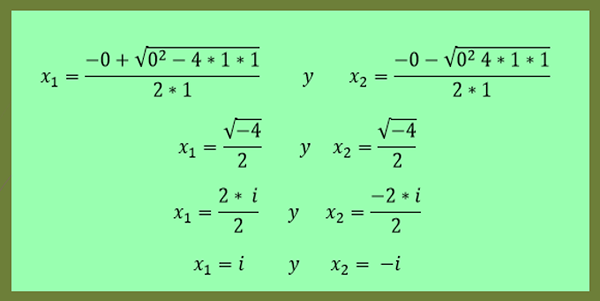
Seperti yang dapat dilihat dalam contoh terakhir ini, X2 adalah konjugat X1.