Halaman rumah
Matematika
DECAGON REGULER, tidak beraturan, properti, contoh

Matematika

DECAGON REGULER, tidak beraturan, properti, contoh

Dia decagon Ini adalah sosok datar dengan poligon -berbentuk 10 sisi dan 10 simpul atau ujung. Decagon dapat menjadi teratur atau tidak teratur, dalam kasus pertama semua sisi dan sudut internal memiliki ukuran yang sama, sedangkan di sisi kedua dan/atau sudutnya berbeda satu sama lain.

Gambar 1 menunjukkan contoh dekagon dari masing -masing jenis dan seperti yang bisa kita lihat, decagon biasa sangat simetris.

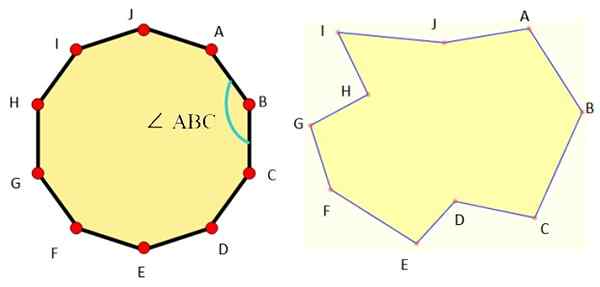Gambar 1. Di sebelah kiri decagon biasa dan di sebelah kanan decagon yang tidak teratur. Sumber: Wikimedia Commons/F. Zapata/Mathpenref.

Elemen dasar semua decagon adalah:

-Sisi, garis garis yang saat bergabung dengan decagon.

-Simpul, atau titik di antara setiap sisi berturut -turut.

-Sudut internal dan eksternal di antara sisi yang berdekatan.

-Diagonals, segmen yang menyatukan dua simpul yang tidak berurutan.

Vertices disebut dengan huruf kapital, seperti yang ditunjukkan pada Gambar 1, di mana huruf pertama alfabet digunakan, tetapi huruf apa pun dapat digunakan.

Sisi dilambangkan dengan dua huruf simpul di antaranya, misalnya sisi AB adalah satu di antara simpul A dan B. Dengan cara yang sama dilakukan dengan diagonal, jadi kami memiliki AF diagonal, yang bergabung dengan titik A dan F.

Untuk sudut kami menggunakan simbol ini: ∠, mirip dengan l yang miring. Misalnya, sudut ∠ ABC adalah yang verteksnya adalah B dan yang sisinya adalah segmen AB dan BC.

[TOC]

Decagon biasa

Di Decagon biasa, semua sisi memiliki ukuran yang sama, serta sudut internal. Oleh karena itu dikatakan sama sisi (sisi yang sama) dan pigura yg sudutnya sama (Sudut yang sama). Itu adalah sosok yang sangat simetris

Sudut interior decagon biasa

Untuk menemukan ukuran sudut internal poligon biasa, termasuk decagon biasa, formula berikut digunakan:

$I=\frac(n-2)\times 180^^on$

Di mana:

-Saya adalah ukuran sudut dalam derajat.

-n adalah jumlah sisi poligon. Dalam kasus decagon n = 10.

Dapat melayani Anda: heptagon

Mengganti n = 10 dalam formula sebelumnya kita mendapatkan yang berikut:

$I=\frac(10-2)\times 180^^o10=144^^o$

Sekarang, dikatakan bahwa poligon adalah cembung Jika langkah -langkah sudutnya kurang dari 180º, jika tidak, poligonnya cekung. Seperti sudut internal setiap decagon reguler berukuran 144º dan kurang dari 180º, maka itu adalah poligon cembung.

Jumlah sudut internal

Jumlah ukuran sudut internal poligon apa pun, dalam derajat:

S = (n-2) x 180º; n selalu lebih besar dari 2

Dalam formula ini kita harus:

-S adalah jumlah dari ukuran sudut internal.

-n adalah jumlah sisi. Untuk decagon n = 10

Menerapkan rumus untuk n = 10 hasil:

S = (10 - 2) x 180º = 1440º

Sudut eksterior

Sudut luar terbentuk antara satu sisi dan ekstensi sisi yang berdekatan, mari kita lihat:

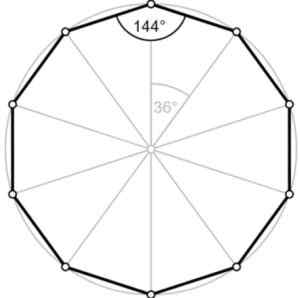
Gambar 2.- Sudut eksternal decagon reguler berukuran 36º. Air mancur. Wikimedia Commons/F. Zapata.

Sudut ∠ ABC ditambah sudut eksternal menambahkan 180º, yaitu, mereka Tambahan. Oleh karena itu sudut eksternal sama dengan 180º-144º = 36º, seperti yang kita lihat pada gambar.

Jumlah diagonal

Seperti yang dinyatakan sebelumnya, diagonal adalah segmen yang menyatukan simpul non -berturut -turut. Berapa banyak diagonal yang bisa kita lacak di sebuah decagon? Ketika jumlah simpul kecil, mereka dapat dengan mudah dihitung, tetapi ketika angka itu meningkat, Anda dapat kehilangan akun.

Untungnya ada formula untuk mengetahui jumlah diagonal yang dimiliki poligon N sisi:

$D=\fracn(n-3)2$

Untuk decagon kami mengganti n = 10 dan dapatkan:

D = 10 x (10 - 3) /2 = 35

Di decagon biasa, semua diagonal dipotong pada satu titik, yang merupakan pusat gambar:

Gambar 3. Sudut dan diagonal decagon biasa. Sumber: Wikimedia Commons.

Tengah

Pusat poligon didefinisikan sebagai titik sama dari setiap simpul. Pada gambar sebelumnya, pusat bertepatan dengan titik persimpangan semua diagonal.

Perimeter

Jika decagon biasa memiliki sisi A, perimeter P adalah jumlah dari semua sisi:

Dapat melayani Anda: 90 pembagi: Apa itu dan penjelasan

P = 10.ke

Daerah

Mengetahui panjangnya ke Di samping, area decagon biasa dihitung oleh:

$A=\left (\frac52 \right )cot\left ( \frac\pi 10 \right )a^2$

Formula perkiraan untuk area tersebut adalah:

$A=\frac10a^24 \times tg\left ( \frac\pi 10 \right )\simeq 7.694a^2$

Dan opsi ketiga untuk menemukan area tersebut adalah dengan panjang apothem l_KE. Ini adalah segmen yang bergabung dengan titik tengah di satu sisi dengan pusat poligon.

Dalam hal ini, area tersebut dapat dihitung menggunakan rumus:

$A=\fracP.L__A2=\frac10a\times L_A2$

Decagon tidak teratur

Decagon yang tidak teratur bukanlah hal yang sama atau sama, dan secara umum tidak memiliki simetri dari gambar reguler, meskipun beberapa dekagon mungkin memiliki sumbu simetri.

Mereka juga bisa cembung atau cekung, jika ada sudut internal yang lebih besar dari 180º.

Dekagon yang tidak teratur dari Gambar 1 adalah cekung, karena beberapa sudut internalnya lebih besar dari 180º. Jelaslah bahwa ada banyak kombinasi sudut dan sisi yang menimbulkan decagon yang tidak teratur.

Bagaimanapun, terpenuhi bahwa:

-Sudut internal decagon yang tidak teratur juga menambahkan 1440º.

-Ini juga memiliki 35 diagonal.

Area deason tidak teratur oleh penentu Gauss

Secara umum tidak ada formula unik untuk menemukan area poligon yang tidak teratur, karena sisi dan sudutnya berbeda. Namun, Anda dapat menemukan mengetahui koordinat simpul dan menghitung Penentu Gauss:

-Mari kita hubungi (x_N , Dan_N) ke koordinat simpul, dengan N bervariasi dari 1 hingga 10.

-Anda dapat mulai dari titik mana pun, ke koordinat mana yang akan ditetapkan (x x₁, Dan₁). Sekarang Anda harus mengganti nilai setiap koordinat dalam rumus ini:

$A=\left |\frac(x_1y_2-x_2y_1)+(x_2y_3-x_3y_2)+(x_3y_4-x_4y_3)+… (x_ny_1-x_1y_n)2 \right |$

Di mana penentu justru operasi antara tanda kurung.

-Penting untuk diperhatikan bahwa penentu terakhir melibatkan simpul pertama bersama dengan yang terakhir. Untuk Decagon, akan seperti ini:

(X₁₀Dan₁ - X₁Dan₁₀)

Dapat melayani Anda: interpolasi lagrange

Penting: Bilah adalah nilai absolut dan berarti bahwa hasil akhir selalu dengan tanda positif.

Prosedur ini bisa melelahkan ketika angka tersebut memiliki banyak simpul, dalam kasus DECAGON ada 10 operasi, sehingga disarankan untuk membuat tabel atau daftar.

Olahraga diselesaikan

Hitung area decagon tidak teratur yang ditunjukkan pada gambar. Koordinat simpul adalah A, B, C ... J, yang nilainya ditunjukkan ke kiri.

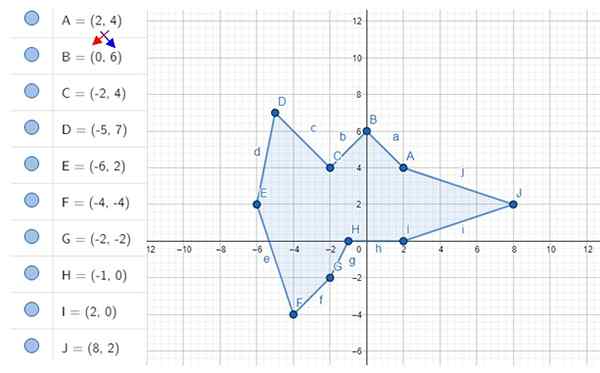Gambar 4. Decagon yang tidak teratur dan simpulnya. Sumber: f. Zapata dengan Geogebra.

Larutan

-Kami membuat masing -masing dari 10 operasi:

2 × 6 - 4 × 0 = 12 - 0 = 12
0 × 4 - 6 × (-2) = 0 + 12 = 12
(-2) × 7- 4 × (-5) = -14 + 20 = 6
(-5) × 2 -7 × (-6) = -10 + 42 = 32
(-6) × (-4) -2 × (-4) = 24 + 8 = 32
(-4) × (-2)-(-4) × (-2) = 8-8 = 0
(-2) × 0-(-2) × (-1) = 0 -2
(-1) × 0 - 0 × (2) = 0 - 0 = 0
2 × 2 - 0 × 8 = 4 - 0 = 4
8 × 4 -2 × 2 = 32 - 4 = 28

-Kami menambahkan hasilnya:

12 + 12 + 6 + 32 + 32 + 0 + (-2) + 0 + 4 + 28 = 124

Hasil positif diperoleh bahkan tanpa batang nilai absolut, tetapi jika negatif, hal yang sama diubah.

-Hasil sebelumnya dibagi dengan 2 dan itu adalah luas poligon:

A = 124/2 = 62

Properti Decangon

Di bawah ini adalah ringkasan sifat umum decagon, baik secara teratur atau tidak teratur:

-Memiliki 10 sisi dan 10 simpul.

-Jumlah sudut internal adalah 1440º.

-Ada 35 diagonal.

-Perimeter adalah jumlah dari semua sisi.

-Anda dapat membuat segitiga di dalam segmen menggambar poligon dari titik ke orang lain. Dalam sebuah decagon dimungkinkan untuk menggambar 8 segitiga dengan cara ini, seperti yang ditunjukkan di bawah ini:

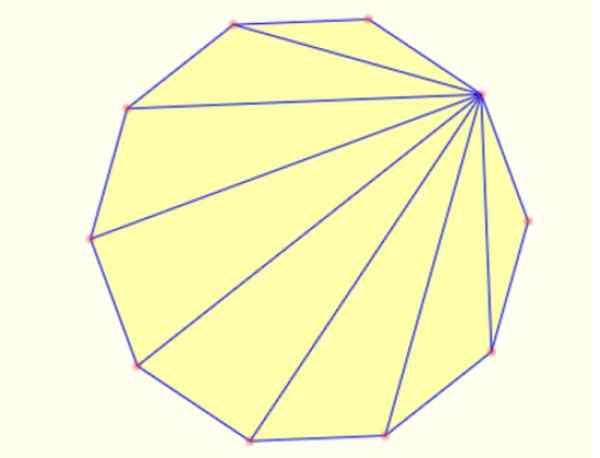Gambar 5. Segitiga internal di decagon biasa. Sumber: Mathpenref.

Referensi

Alexander, d. 2013. Geometri. Ke -5. Edisi. Pembelajaran Cengage.
Decagon.com. Decagon. Pulih dari: decagon.com
Referensi Terbuka Matematika. Decagon. Pulih dari: mathpenref.com.
Matematika Sangaku. Elemen poligon dan klasifikasinya. Pulih dari: sangakoo.com.
Wikipedia. Decagon. Pulih dari: is.Wikipedia.com.