Berasal dari perhitungan cotangent, demonstrasi, latihan

Itu Diturunkan cotangent Itu sama dengan kebalikan dari kuadrat panen “-csc²". Formula ini disebabkan oleh hukum turunan menurut definisi dan diferensiasi fungsi trigonometri. Itu dilambangkan sebagai berikut:

D (ctg u) = -csc² atau . du

Di mana "du" melambangkan ekspresi yang berasal dari fungsi argumen, sehubungan dengan variabel independen.

Sumber: Pixabay.com

[TOC]

Bagaimana itu dihitung?

Prosedur untuk mengembangkan turunan ini cukup sederhana. Hanya mengidentifikasi argumen dan jenis fungsi yang diwakilinya.

Misalnya, ekspresi CTG (F/G) menyajikan pembagian dalam argumennya. Ini membutuhkan diferensiasi tentang u/v, setelah mengembangkan zip.

Cotangent adalah fungsi timbal balik dari garis singgung. Aljabar ini berarti bahwa:

(1/tg x) = ctg x

Ctg x = cos x / sen x

Tidak benar untuk mengatakan bahwa fungsi cotangent adalah "terbalik" dari garis singgung. Ini karena fungsi terbalik dari garis singgung menurut definisi adalah busur singgung.

(Tg^-1 x) = arctg x

Menurut trigonometri Pythagoras, cotangent terlibat dalam bagian berikut:

CTG x = (cos x) / (sin x)

CTG² X + 1 = csc² X

Menurut trigonometri analitik menanggapi identitas berikut:

CTG (A + B) = (1 - TG a . Tg b) / (tg a + tg b)

CTG (A - B) = (1 + TG a . Tg b) / (tg a - tg b)

CTG (2A) = (1 - TG² a) / (2tg a)

Karakteristik fungsi cotangent

Penting untuk menganalisis berbagai karakteristik fungsi f (x) = CTG X untuk dapat menentukan aspek yang diperlukan untuk mempelajari diferensiasi dan penerapannya.

Asimtot vertikal

Fungsi cotangent tidak didefinisikan dalam nilai -nilai yang membuat ekspresi "sen" nol. Karena CTG x = (cos x) / (sin) yang setara, ia akan memiliki ketidakpastian di semua "nπ" dengan n milik bilangan bulat.

Itu dapat melayani Anda: geometri analitik

Yaitu, dalam masing -masing nilai x = nπ ini akan ada asimptot vertikal. Saat nilai pendekatan cotangent, dan saat mendekati hak, fungsi akan meningkat tanpa batas waktu.

Domain

Domain fungsi cotangent diekspresikan oleh set x ∈ R / x ≠ nπ, n ∈ Z. Ini dibaca sebagai "X milik set bilangan real sedemikian rupa sehingga, x berbeda dari nπ, dengan n milik seluruh seluruh angka".

Jangkauan

Peringkat fungsi cotangent mencakup dari kurang hingga lebih tak terbatas. Itulah mengapa dapat disimpulkan bahwa peringkatnya adalah himpunan angka N nyata.

Frekuensi

Fungsi cotangent bersifat periodik dan periodenya sama dengan π. Dengan cara ini kesetaraan CTG x = CTG (x + nπ) dipenuhi, di mana n milik z.

Perilaku

Ini adalah fungsi yang aneh, karena ctg (-x) = - ctg x. Dengan cara ini diketahui bahwa fungsi menyajikan simetri sehubungan dengan asal koordinat. Ini juga menyajikan penurunan setiap interval yang terletak di antara 2 asimtot vertikal berturut -turut.

Itu tidak memiliki nilai maksimum atau minimum, karena pendekatannya terhadap asimtot vertikal memiliki perilaku di mana fungsi tumbuh atau berkurang tanpa batas waktu.

Nol atau akar fungsi cotangent ditemukan dalam kelipatan ganjil π/2. Ini berarti bahwa CTG x = 0 dipenuhi dalam nilai -nilai bentuk x = nπ/2 dengan keseluruhan.

Demonstrasi

Ada 2 cara untuk menunjukkan turunan dari fungsi cotangent.

Demonstrasi diferensial trigonometri

Turunan fungsi cotangent ditunjukkan dari yang setara di payudara dan cosenos.

Dapat melayani Anda: Aljabar Boolean: Sejarah, Teorema dan Deposulat, Contoh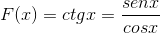

Ini tentang turunan dari divisi fungsi

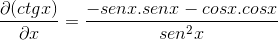
Setelah menurunkan faktor dikelompokkan dan identitas Pythagoras dicari untuk ditiru

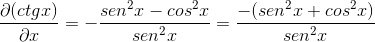
Mengganti identitas dan menerapkan timbal balik ekspresi diperoleh

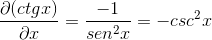
Definisi Definisi Derivatif

Ekspresi berikut sesuai dengan turunan menurut definisi. Di mana jarak antara 2 titik fungsi mendekati nol.

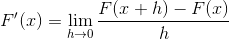
Mengganti Cotangente Anda harus:

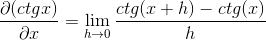
Identitas berlaku untuk jumlah argumen dan timbal balik

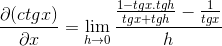
Fraksi pembilang dioperasikan secara tradisional

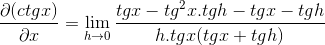
Menghilangkan elemen yang berlawanan dan menarik faktor umum diperoleh

Menerapkan identitas dan timbal balik Pythagoras

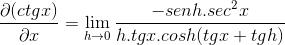
Elemen yang dievaluasi dalam X adalah konstan sehubungan dengan batas, oleh karena itu mereka dapat meninggalkan argumen ini. Kemudian batas trigonometri diterapkan.

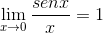
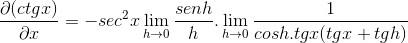
Batas dievaluasi

Maka itu memperhitungkan sampai mencapai nilai yang diinginkan

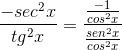
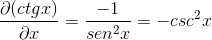
Ini ditunjukkan oleh turunan Cotangente sebagai kebalikan dari kuadrat pemanen.

Latihan terpecahkan

Latihan 1

Menurut fungsi f (x), tentukan ekspresi f '(x)

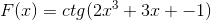
Derivasi yang sesuai diterapkan menghormati aturan rantai

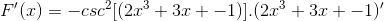
Mendapatkan argumen

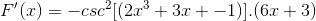
Terkadang perlu menerapkan identitas timbal balik atau trigonometri untuk mengadaptasi solusi.

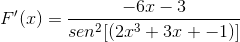
Latihan 2

Tentukan ekspresi diferensial yang sesuai dengan f (x)

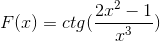
Menurut formula derivasi dan menghormati aturan rantai

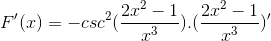
Argumen diturunkan, sedangkan sisanya tetap sama

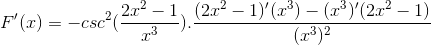
Mendapatkan semua elemen

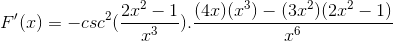
Beroperasi dengan cara tradisional produk dari basis yang sama

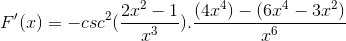
Elemen yang sama ditambahkan dan faktor umum diekstraksi

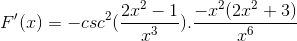
Tanda disederhanakan dan dioperasikan. Memberi jalan pada ekspresi yang benar -benar diturunkan

Dapat melayani Anda: perbedaan antara fraksi umum dan angka desimal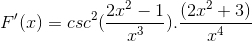

Referensi

1. Seri Trigonometrik, Volume 1. KE. Zygmund. Cambridge University Press, 2002
2. Kalkulus variabel tunggal. Ron Larson, Bruce H. Edwards. Pembelajaran Cengage, 10 Nov. 2008
3. Kalkulus dengan trigonometri dan geometri analitik. John h. Saxon, John Saxon, Frank Wang, Diana Harvey. Saxon Publishers, 1988
4. Analisis multivariabel. Sable Shirali, Harkrishan Lal Vasudeva. Springer Science & Business Media, 13 Desember. 2010
5. Dinamika Sistem: Pemodelan, Simulasi, dan Kontrol Sistem Mekatronik. Dean c. Karnopp, Donald L. Margolis, Ronald C. Rosenberg. John Wiley & Sons, 7 Mar. 2012
6. Kalkulus: Matematika dan Pemodelan. William Bauldry, Joseph R. Fiedler, Frank R. Giordano, Ed Lodi, Rick Vitray. Addison Wesley Longman, 1 Januari. 1999