Derivatif berturut -turut

Apa turunannya yang berurutan?

Itu Derivatif berturut -turut Mereka adalah yang berasal dari suatu fungsi setelah turunan kedua. Proses untuk menghitung turunan berturut -turut adalah sebagai berikut: Ada fungsi F, yang dapat kita dapatkan dan mendapatkan fungsi yang diturunkan f '. Untuk turunan ini dari kita dapat memperolehnya lagi, memperoleh (f ')'.

Fungsi baru ini disebut turunan kedua; Semua turunan yang dihitung dari yang kedua berturut -turut; Ini, juga disebut orde yang lebih tinggi, memiliki aplikasi besar, seperti memberikan informasi tentang stroke grafik fungsi, uji turunan kedua untuk ujung relatif dan penentuan seri tak terbatas.

Definisi

Menggunakan notasi Leibniz, kami memiliki turunan dari fungsi "y" sehubungan dengan "x" adalah dy/dx. Untuk mengekspresikan turunan kedua "y" menggunakan notasi Leibniz, kami menulis sebagai berikut:

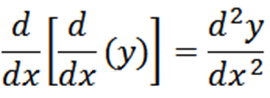
Secara umum, kita dapat mengekspresikan turunan berturut -turut sebagai berikut dengan notasi Leibniz, di mana N mewakili urutan turunan.

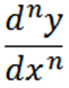
Notasi lain yang digunakan adalah sebagai berikut:

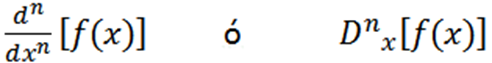
Beberapa contoh di mana kita dapat melihat notasi yang berbeda adalah:

Contoh 1

Dapatkan semua turunan dari fungsi F yang ditentukan oleh:

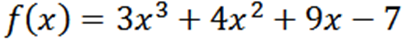
Menggunakan teknik rujukan biasa, kami memiliki bahwa f adalah:

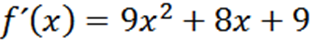
Mengulangi proses kita bisa mendapatkan turunan kedua, turunan ketiga dan sebagainya.

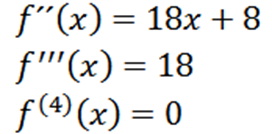
Perhatikan bahwa turunan keempat adalah nol dan turunan nol adalah nol, jadi kita harus:

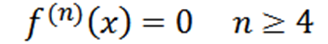
Contoh 2

Hitung yang keempat yang berasal dari fungsi berikut:

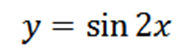
Menurunkan fungsi yang kita miliki sebagai hasilnya:

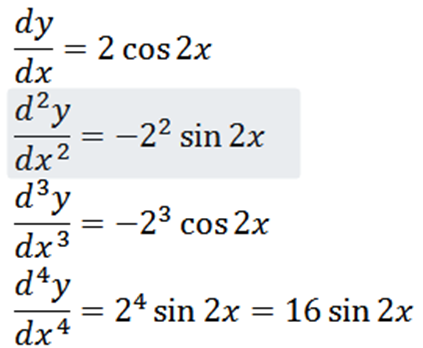
Kecepatan dan percepatan

Salah satu motivasi yang mengarah pada penemuan turunannya adalah pencarian definisi kecepatan instan. Definisi formal adalah sebagai berikut:

Dapat melayani Anda: bilangan primo: karakteristik, contoh, latihan

Biarkan y = f (t) fungsi yang grafiknya menjelaskan lintasan partikel dalam sekejap T, Kemudian kecepatannya pada saat t diberikan oleh:

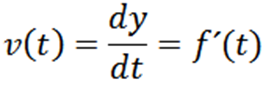
Setelah kecepatan partikel diperoleh, kita dapat menghitung akselerasi instan, yang didefinisikan sebagai berikut:

Akselerasi partikel sesaat yang lintasannya diberikan oleh y = f (t) adalah:

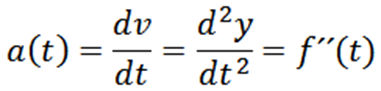
Contoh 1

Partikel bergerak pada garis sesuai dengan fungsi posisi:

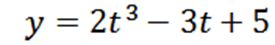
Di mana "y" diukur dalam meter dan "t" dalam hitungan detik.

• Pada saat apa kecepatan Anda adalah 0?
• Pada saat apa akselerasinya adalah 0?

Dengan mendapatkan fungsi posisi "y", kami memiliki kecepatan dan akselerasinya masing -masing diberikan oleh:

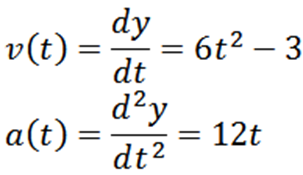
Untuk menjawab pertanyaan pertama, itu cukup untuk menentukan kapan fungsi V V adalah nol; ini:

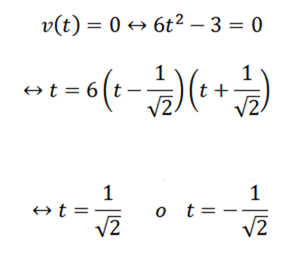
Kami melanjutkan dengan pertanyaan berikutnya analog:

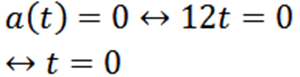
Contoh 2

Sebuah partikel bergerak pada garis sesuai dengan persamaan gerakan berikut:

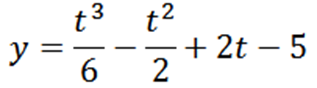
Tentukan "t, y" dan "v" saat a = 0.

Mengetahui kecepatan dan akselerasi itu diberikan oleh

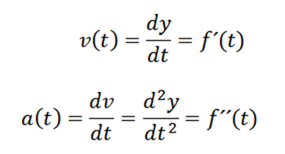
Kami melanjutkan untuk mendapatkan dan memperoleh:

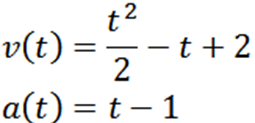
Melakukan a = 0, kami memiliki:

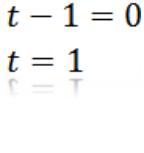
Di mana kita dapat menyimpulkan bahwa nilai t sehingga a sama dengan nol adalah t = 1.

Kemudian, mengevaluasi t = 1 posisi dan fungsi fungsi, kita harus:

Aplikasi

Derivasi Mplícita

Derivatif berturut -turut juga dapat diperoleh dengan derivasi implisit.

Contoh

Mengingat elips berikut, temukan "y":

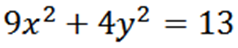
Secara implisit berasal sehubungan dengan x, kami memiliki:

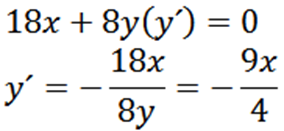
Kemudian, kembali secara implisit sehubungan dengan X, memberi kita:

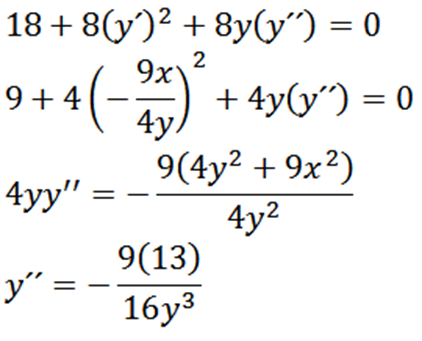
Akhirnya, kami memiliki:

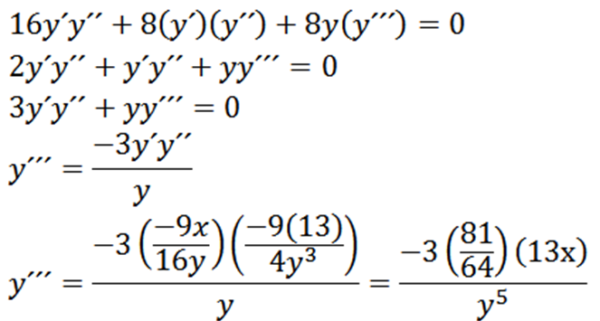
Ekstrem relatif

Penggunaan lain yang dapat kita berikan pada turunan urutan kedua adalah dalam perhitungan ujung relatif suatu fungsi.

Dapat melayani Anda: berapa banyak sumbu simetri yang dimiliki lingkaran?

Kriteria turunan pertama untuk ekstrem lokal memberi tahu kita bahwa jika kita memiliki fungsi F kontinu dalam interval (a, b) dan ada C yang termasuk interval yang disebutkan sehingga dibatalkan dalam C (yaitu, c itu adalah titik kritis), salah satu dari tiga kasus ini dapat terjadi:

• Jika f '(x)> 0 untuk setiap x milik (a, c) dan f' (x)<0 para x perteneciente a (c,b), entonces f(c) es un máximo local.
• Jika f '(x) 0 untuk x milik (c, b), maka f (c) adalah minimum lokal.
• Jika f '(x) memiliki tanda yang sama (a, c) dan dalam (c, b), itu menyiratkan bahwa f (c) bukan ujung lokal.

Menggunakan kriteria turunan kedua, kita dapat mengetahui jika sejumlah fungsi kritis adalah minimum maksimum atau lokal, tanpa harus melakukan apa tanda fungsi pada interval yang disebutkan di atas.

Kriteria drift kedua memberi tahu kita bahwa jika f '(c) = 0 dan bahwa f "(x) kontinu dalam (a, b), itu terjadi jika f" (c)> 0 maka f (c) adalah a Minimum lokal dan jika f "(c) < 0 entonces f(c) es un máximo local.

Jika f "(c) = 0, kita tidak dapat menyimpulkan apapun.

Contoh

Mengingat fungsi f (x) = x⁴ + (4/3) x³ - 4x², Temukan kerabat maksimum dan minimum F yang menerapkan kriteria turunan kedua.

Pertama kami menghitung f '(x) dan f "(x) dan kami memiliki:

f '(x) = 4x³ + 4x² - 8x

f "(x) = 12x² + 8x - 8

Sekarang, f '(x) = 0 ya, dan hanya jika 4x (x + 2) (x - 1) = 0, dan ini terjadi ketika x = 0, x = 1 atau x = - 2.

Untuk menentukan apakah angka -angka kritis yang diperoleh relatif ekstrem yang hanya dievaluasi dalam f "dan dengan demikian mengamati tandanya.

Dapat melayani Anda: heptagon

f "(0) = - 8, jadi f (0) adalah maksimum lokal.

f "(1) = 12, jadi f (1) adalah minimum lokal.

f "(- 2) = 24, jadi f (- 2) adalah minimum lokal.

Seri Taylor

Menjadi fungsi yang didefinisikan sebagai berikut:

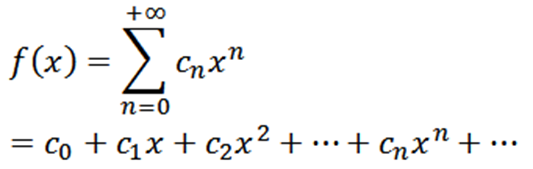
Fungsi ini memiliki jari-jari konvergensi R> 0 dan telah berasal dari semua pesanan di (-r, r). Derivatif berturut -turut dari F memberi kita:

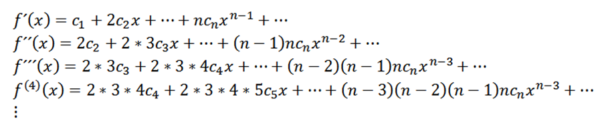
Mengambil x = 0, kita bisa mendapatkan nilai c_N tergantung pada turunannya sebagai berikut:

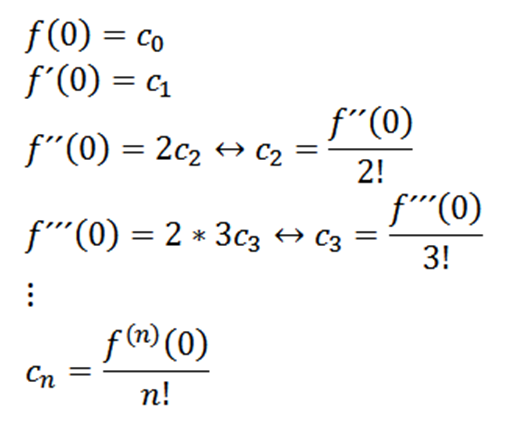
Jika kita mengambil n = 0 sebagai fungsi f (yaitu, f^0 = f), maka kita dapat menulis ulang fungsi sebagai berikut:

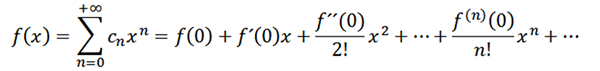
Sekarang mari kita pertimbangkan fungsinya sebagai serangkaian kekuatan di x = a:

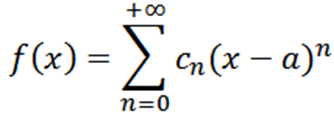
Jika kami melakukan analisis yang analog dengan yang sebelumnya, kami harus menulis fungsi f sebagai:

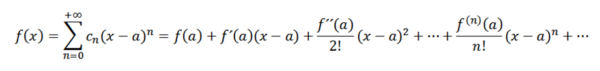
Seri ini dikenal sebagai Taylor F dalam seri. Ketika a = 0 kita memiliki kasus tertentu yang disebut seri MacLaurin. Jenis seri ini sangat penting matematis terutama dalam analisis numerik, karena berkat ini kita dapat mendefinisikan fungsi di komputer seperti E^X , sin (x) dan cos (x).

Contoh

Dapatkan Seri Maclaurin untuk E^X.

Perhatikan bahwa jika f (x) = e^X, lalu f^(N)(x) = e^X dan f^(N)(0) = 1, jadi seri Maclaurin Anda adalah: