Matematika

Ketidaksetaraan segitiga demonstrasi, contoh, latihan diselesaikan

Ketidaksetaraan segitiga demonstrasi, contoh, latihan diselesaikan

Itu disebut Ketidaksetaraan segitiga ke properti yang memenuhi dua bilangan real yang terdiri dari nilai absolut dari jumlahnya selalu kurang dari atau sama dengan jumlah nilai absolutnya. Properti ini juga dikenal sebagai ketidaksetaraan Minkowski atau ketidaksetaraan segitiga.

Properti angka ini disebut ketidaksetaraan segitiga karena dalam segitiga itu terjadi bahwa panjang satu sisi selalu kurang dari atau sama dengan jumlah dua lainnya, bahkan jika ketidaksetaraan ini tidak selalu berlaku di bidang segitiga.

Gambar 1. Nilai absolut dari jumlah dua angka selalu kurang dari atau sama dengan jumlah nilai absolutnya. (Disiapkan oleh r. Pérez)

Ada beberapa demonstrasi ketidaksetaraan segitiga dalam bilangan real, tetapi dalam hal ini kita akan memilih A berdasarkan sifat -sifat nilai absolut dan binomial kuadrat.

Dalil: Untuk semua pasangan angka ke Dan B Milik bilangan real, itu harus:

| A + B | ≤ | A | + | B |

[TOC]

Demonstrasi

Kami mulai dengan mempertimbangkan anggota pertama dari ketidaksetaraan, yang akan ditebang:

| A + B |^2 = (A + B)^2 = A^2 + 2 A B + B^2 (EC. 1)

Pada langkah sebelumnya, properti telah digunakan bahwa angka apa pun yang tinggi ke kuadrat sama dengan nilai absolut dari angka tersebut tinggi ke kuadrat, yaitu: | x |^2 = x^2. Pengembangan binomial persegi juga telah digunakan.

Semua angka X Itu kurang dari atau sama dengan nilai absolutnya. Jika angkanya positif, itu layak untuk kesetaraan, tetapi jika angkanya negatif, itu akan selalu kurang dari angka positif. Dalam hal ini nilai absolutnya sendiri, artinya itu dapat dinyatakan itu x ≤ | x |.

Dapat melayani Anda: pemrograman non -linier: metode dan latihan

Produk (a b) Itu adalah angka, oleh karena itu diterapkan bahwa (a b) ≤ | A B |. Saat properti ini diterapkan pada (EC. 1) Kami memiliki:

| A + B |^2 = A^2 + 2 (A B) + B^2 ≤ A^2 + 2 | A B | + B^2 (EC. 2)

Mempertimbangkan itu | A B | = | A || B | La (EC. 2) Ini dapat ditulis sebagai berikut:

 | A + B |^2 ≤ A^2 + 2 | A || B | + B^2 (EC. 3)

Tetapi seperti yang telah kami katakan sebelumnya bahwa kuadrat angka sama dengan nilai absolut angka tinggi ke kuadrat, maka Persamaan 3 dapat ditulis ulang sebagai berikut:

 | A + B |^2 ≤ | A |^2 + 2 | A | | B | + | B |^2 (EC. 4)

Pada anggota kedua ketidaksetaraan, produk yang luar biasa diakui, yang ketika diterapkan mengarah pada:

 | A + B |^2 ≤ (| A | + | B |)^2 (EC. 5)

Dalam ungkapan sebelumnya, harus dicatat bahwa nilai -nilai yang akan dinaikkan pada kedua anggota ketidaksetaraan juga positif bahwa itu juga harus dipenuhi bahwa:

 | A + B | ≤ (| a |+ | b |) (EC. 6)

Ekspresi sebelumnya adalah persis apa yang ingin Anda tunjukkan.

Contoh

Selanjutnya kita akan memeriksa ketimpangan segitiga dengan beberapa contoh.

Contoh 1

Nilai diambil a = 2 dan nilai b = 5, yaitu angka positif dan kami memverifikasi apakah ketidaksetaraan terpenuhi atau tidak.

 | 2 + 5 | ≤ | 2 |+ | 5 |

 | 7 | ≤ | 2 |+ | 5 |

7 ≤ 2+ 5

Kesetaraan diverifikasi, oleh karena itu teorema ketimpangan segitiga telah terpenuhi.

Contoh 2

Nilai -nilai berikut dipilih a = 2 dan b = -5, yaitu angka positif dan negatif lainnya, kami memeriksa apakah ketidaksetaraan terpenuhi atau tidak.

Dapat melayani Anda: trinomial

 | 2 - 5 | ≤ | 2 |+ | -5 |

 | -3 | ≤ | 2 |+ | -5 |

 3 ≤ 2 + 5

Ketidaksetaraan terpenuhi, oleh karena itu teorema ketimpangan segitiga telah diverifikasi.

Contoh 3

Nilai diambil A = -2 dan nilai b = 5, yaitu angka negatif dan positif lainnya, kami memverifikasi apakah ketidaksetaraan terpenuhi atau tidak.

 | -2 + 5 | ≤ | -2 |+ | 5 |

 | 3 | ≤ | -2 |+ | 5 |

 3 ≤ 2 + 5

Ketidaksetaraan diverifikasi, oleh karena itu teorema telah terpenuhi.

Contoh 4

Nilai -nilai berikut A = -2 dan B = -5 dipilih, yaitu, keduanya angka negatif dan kami memeriksa apakah ketidaksetaraan terpenuhi atau tidak.

 | -2 - 5 | ≤ | -2 |+ | -5 |

 | -7 | ≤ | -2 |+ | -5 |

 7 ≤ 2+ 5

Kesetaraan diverifikasi, oleh karena itu teorema ketimpangan Minkowsk telah terpenuhi.

Contoh 5

Nilai diambil a = 0 dan nilai b = 5, yaitu angka nol dan positif lainnya, maka kami memeriksa apakah ketidaksetaraan terpenuhi atau tidak.

 | 0 + 5 | ≤ | 0 |+ | 5 |

 | 5 | ≤ | 0 |+ | 5 |

 5 ≤ 0+ 5

Kesetaraan terpenuhi, oleh karena itu teorema ketimpangan segitiga telah diverifikasi.

Contoh 6

Nilai diambil A = 0 dan nilai b = -7, yaitu angka nol dan positif lainnya, maka kami memeriksa apakah ketidaksetaraan terpenuhi atau tidak.

 | 0 - 7 | ≤ | 0 |+ | -7 |

 | -7 | ≤ | 0 |+ | -7 |

 7 ≤ 0+ 7

Kesetaraan diverifikasi, oleh karena itu teorema ketimpangan segitiga telah terpenuhi.

Latihan terpecahkan

Dalam latihan berikut secara geometris mewakili ketidaksetaraan segitiga atau ketidaksetaraan Minkowski untuk angka A dan B.

Dapat melayani Anda: papomudas

Angka A akan direpresentasikan sebagai segmen pada sumbu x, asal atau bertepatan dengan nol sumbu x dan ujung lainnya dari segmen (pada titik p) akan berada dalam arah positif (ke kanan) dari x sumbu jika a> 0, tapi untuk < 0 estará hacia la dirección negativa del eje X, tantas unidades como indique su valor absoluto.

Demikian pula, angka B akan direpresentasikan sebagai segmen yang asalnya pada titik p. Ujung lain, yaitu, titik yang akan ke kanan p jika b positif (b> 0) dan titik Q akan menjadi | B | unit di sebelah kiri p jika b<0.

Latihan 1

Secara grafis mewakili ketidaksetaraan segitiga untuk a = 5 dan b = 3 | A + B | ≤ | A | + | B |, makhluk C = a + b. 

Solusi 1: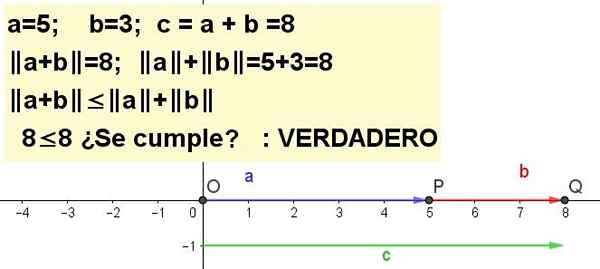

Latihan 2

Buat grafik ketimpangan segitiga untuk a = 5 dan b = -3. 

| A + B | ≤ | A | + | B |, makhluk C = a + b.

Solusi 2:

Latihan 3

Grafik ketidaksetaraan segitiga untuk a = -5 dan b = 3.

| A + B | ≤ | A | + | B |, makhluk C = a + b. 

Solusi 3: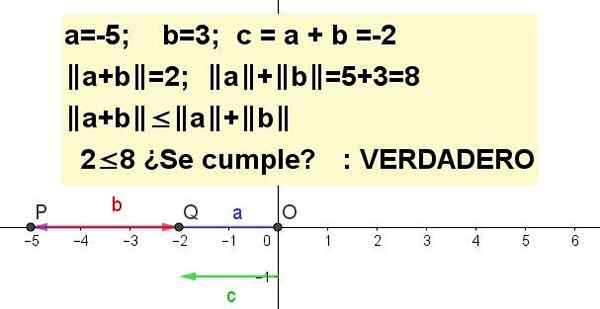

Latihan 4

Grafik ketimpangan segitiga untuk a = -5 dan b = -3.

| A + B | ≤ | A | + | B |, makhluk C = a + b.

Solusi 4: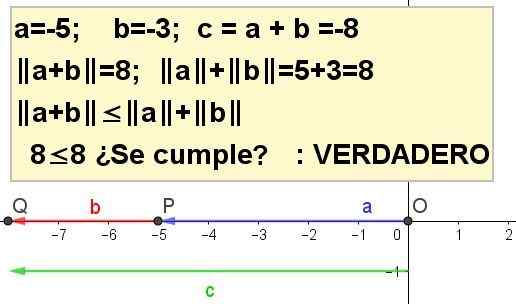

Referensi

  1. DAN. Whitesitt. (1980).Aljabar boolean dan aplikasinya . Perusahaan Editorial Kontinental C. KE.
  2. Mícheal atau 'searcoid.(2003) Elemen Analisis Abstrak ... Departemen Matematika. University College Dublin, Beldfield, Dublind.
  3. J. Van Wyk. (2006) Matematika dan Teknik dalam Ilmu Komputer. Institut Ilmu Komputer dan Teknologi. Biro Standar Nasional. Washington, d. C. 20234
  4. Eric Lehman. Matematika untuk Ilmu Komputer.  Google Inc.
  5. F Thomson Leighton (1980). Kalkulus. Departemen Matematika dan Laboratorium Ilmu Komputer dan Laboratorium AI, Institut Teknologi Massachussetts.
  6. Akademi Khan. Teorema Ketimpangan Segitiga. Pulih dari: Khanacademy.org
  7. Wikipedia. Ketimpangan segitiga. Pulih dari: is. Wikipedia.com