Perpindahan sudut

Apa itu perpindahan sudut?

Dia Perpindahan sudut Ini adalah perubahan atau variasi dalam posisi sudut yang menjadi objek dalam pengalaman rotasi, biasanya diukur dalam radian atau ukuran lain yang diberikan untuk belokan, seperti nilai atau revolusi.

Ketika suatu objek berputar di sekitar sumbu tetap, perpindahan sudutnya ditentukan dengan mengukur sudut yang disapu oleh garis yang melewati titik mana pun dari tubuh yang memotong sumbu rotasi, yaitu, garis radial.

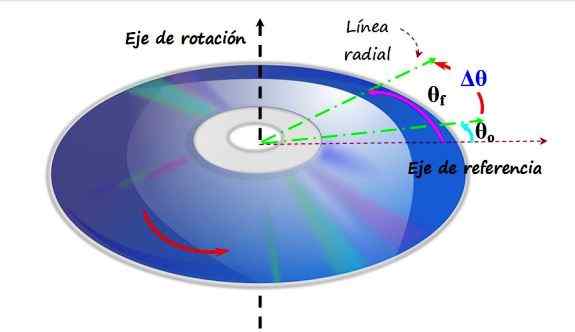Disk ringkas atau CD berputar dalam arah antihoranant di sekitar sumbu rotasi vertikal. Saat beralih dari sudut θo ke θf, dikatakan bahwa ia telah mengalami perpindahan sudut. Sumber: f. Zapata.

Pada gambar atas ada CD yang berputar ke arah anti -hororer, menjadi sumbu rotasi sumbu vertikal. Sumbu referensi ditempatkan pada bidang CD, yang sesuai dengan radian sudut 0 atau 0. Garis hijau adalah garis radial, yang awalnya membentuk sudut θ_{salah satu} Dengan referensi. Ini adalah posisi awal Anda.

Kemudian garis hijau bergerak ke posisi baru yang disebut θ_F, Dan pengalaman yang dialami, yang disebut Δθ sederhana:

Δθ = θ_F - θ_{salah satu}

Setiap titik P dari CD mengalami perpindahan sudut yang sama dalam interval waktu tertentu, kecuali pusat, yang merupakan tempat sumbu rotasi melewati dan tetap diam.

Rumus dan Persamaan

Ada objek yang berputar di sekitar sumbu tetap atau yang meninggalkan layar ke pembaca. Dan di dalamnya, ada titik P, yang terletak pada jarak r dari sumbu rotasi dan menggambarkan lingkaran radio R.

Ini terlihat pada gambar berikut, yang menunjukkan objek pemotongan, terlihat bertentangan dengan jarum jam. Titik yang dipertanyakan adalah pada posisi sudut θ, diukur dari sumbu referensi, yang dalam hal ini adalah sumbu horizontal.

Dapat melayani Anda: prinsip aditif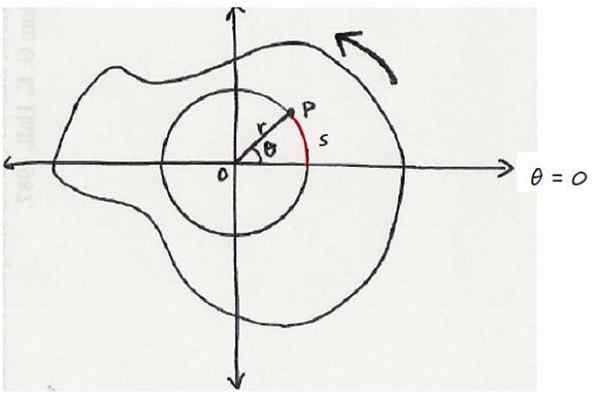Objek yang berputar dalam arti anti -samudra. Sumbu rotasi keluar tegak lurus terhadap layar. Sumber: Wikimedia Commons.

Dengan konvensi, ke rotasi dalam arti anti -thoraria itu diberi akal positif, sedangkan rotasi dalam jadwal memiliki tanda negatif.

Sebagai titik p bersumpah sudut θ, itu secara bersamaan menempuh busur. Karena θ adalah sudut pusat, karena simpulnya menempati pusat keliling, dipenuhi bahwa:

Dengan θ diekspresikan dalam radianes.

Perpindahan sudut adalah:

Δθ = θ_terakhir  - θ_awal

Misalnya, jika P dimulai dengan θ_awal = 0 rad dan kemudian ada di θ_terakhir = 0.8 rad, perpindahan sudutnya berasal dari:

Δθ = 0.8 rad - 0 rad =  0.8 rad

Titik lain dari objek dapat menempati posisi sudut yang berbeda, tetapi semua mengalami perpindahan sudut yang sama. Namun, partikel paling terpencil dari tengah melakukan perjalanan jarak yang lebih jauh, karena S = r⋅θ.

Mengukur sudut

Dalam rotasi adalah umum untuk menemukan sudut yang diukur dalam radian, tetapi mereka juga ditemukan dalam derajat dan revolusi atau belokan. Dalam pemecahan masalah, perlu dipindahkan dari unit -unit ini ke Radianes.

1 Revolusi setara dengan belokan total, yaitu, ketika belokan total pecah, telah berubah 360 º dan ini setara dengan 2π radian, karena dalam hal ini, titik tur busur yang sama dengan 2πr:

Tetapi menyederhanakan, kesetaraan sebelumnya dapat dinyatakan sebagai berikut:

π Radianes = 180º

Bagaimana perpindahan sudut dihitung?

Perpindahan sudut dapat dihitung secara analog dengan bagaimana perpindahan dalam gerakan dihitung dalam dimensi, mengikuti model gerakan tertentu. Untuk ini, kecepatan sudut rata -rata didefinisikan sebagai perpindahan sudut Δθ dalam interval waktu tertentu Δt:

Di mana kecepatan sudut rata -rata dilambangkan sebagai Ω_M dan diberikan dalam radian/s dalam satuan sistem internasional jika.

Dapat melayani Anda: cara mendapatkan sudut segitiga? (Contoh)

Kecepatan sudut instan adalah batas kecepatan sudut rata -rata saat Δt → 0:

Yaitu, ini adalah yang pertama berasal dari posisi sudut sehubungan dengan waktu. Pada gilirannya, akselerasi sudut dapat didefinisikan, dilambangkan sebagai α, yang setara dengan turunan atau laju perubahan kecepatan sudut sehubungan dengan waktu:

Yang juga dapat diartikan sebagai yang kedua berasal dari posisi sudut sehubungan dengan waktu.

Yang penting adalah bahwa dua model gerakan dapat ditetapkan dalam analogi dengan gerakan bujursangkar, karena meskipun rotasi dilakukan di bidang, koordinat sudut tunggal cukup untuk menetapkan posisi titik mana pun dari objek.

Gerakan melingkar seragam

Dalam gerakan melingkar seragam, kecepatan sudut adalah konstan, yaitu, kecepatan sudut rata -rata sama dengan kecepatan sudut instan. Karena akselerasi sudut α sama dengan 0, Anda dapat menulis persamaan berikut untuk posisi sebagai fungsi waktu:

θ = θ_{salah satu} + ωt

Dimana θ_{salah satu} Itu adalah posisi awal ponsel.

Gerakan melingkar yang dipercepat secara seragam

Dalam hal ini, akselerasi sudut α adalah konstan, dan dalam analogi dengan gerakan bujursangkar yang bervariasi secara seragam, persamaan berikut dapat ditulis:

• θ = θ_{salah satu} + Ω_{salah satu} T + ½ αt²
• Ω = Ω_{salah satu} + αt 
• Ω² = Ω_{salah satu}² + 2α ∙ Δθ

Olahraga diselesaikan

Latihan Pertama

Dapat diasumsikan bahwa Bumi adalah objek kaku yang berputar pada sumbu tetap dan rotasinya hampir seragam. Dalam interval waktu Δt = 12 jam temukan:

a) Perpindahan sudut bumi

b) Kecepatan sudut Anda

c) percepatan sudut selama interval waktu itu.

Solusi untuk

Mengetahui bahwa dalam 24 jam Bumi mengambil putaran total di porosnya, dalam 12 jam Anda akan berubah setengah dari satu putaran, yaitu, π Radianes. Jika dianggap sebagai bagian dari θ_awal = 0 rad, maka perpindahan sudutnya adalah:

Dapat melayani Anda: Prinsip Multiplikasi: Teknik dan Contoh Penghitungan

Δθ = π radian

Solusi b

Karena rotasi seragam, kecepatan sudut adalah hasil bagi antara perpindahan sudut dan waktu, selain itu, 1 jam = 3600 s:

Ω = π rad / 12 jam = π rad / (12 x 3600) s = 0.000073 rad/s.

Solusi c

Akselerasi sudut batal, karena rotasi bumi seragam.

Latihan kedua

Juan telah menempuh jarak 35 meter di jalur atletik melingkar yang jari -jarinya sama dengan 7 meter. Hitung perpindahan sudut yang telah dibuat Juan.

Larutan

Karena jarak lengkungan yang ditempuh dan jari -jari keliling diketahui, formula kedua dapat diterapkan untuk mengetahui perpindahan sudut yang dibuat oleh Juan. Menggunakan rumus yang dijelaskan di atas, Anda harus θ = 35/7 = 5 radian.

Latihan ketiga

Jika Mario harus di dalam kendaraannya, setengah dari jalur balap melingkar, apa perpindahan sudut yang telah dilakukan Mario?

Larutan

Dalam latihan ini formula pertama akan berlaku. Karena diketahui bahwa Mario telah menempuh setengah dari trek, dapat diasumsikan bahwa ia memulai balapan di sudut 0 ° dan ketika ia mencapai setengah dari keliling ia telah melakukan perjalanan 180 °. Oleh karena itu, jawabannya adalah 180 ° -0 ° = 180 ° = π radian.

Latihan Keempat

Maria memiliki kolam bundar. Anjing Anda berlari di sekitar kolam renang menempuh jarak 18 meter. Jika jari -jari kolam renang 3 meter, apa perpindahan sudut yang dibuat oleh hewan peliharaan Maria?

Larutan

Karena kolamnya melingkar dan jari -jari diketahui, Anda dapat melanjutkan untuk menggunakan formula kedua.

Diketahui bahwa jari -jari sama dengan 3 meter, dan jarak yang ditempuh oleh hewan peliharaan sama dengan 18 meter. Oleh karena itu, perpindahan sudut yang dilakukan sama dengan θ = 18/3 = 6 radian.

Referensi

1. Katz, d. 2013. Fisika untuk Ilmuwan dan Insinyur. Yayasan dan Koneksi. Pembelajaran Cengage.
2. Rex, a. 2011. Dasar -dasar fisika. Pearson.
3. Sears, Zemansky. 2016. Fisika Universitas dengan Fisika Modern. 14. Ed. Volume 1. Pearson.
4. Serway, r., Jewett, J. (2008). Fisika untuk Sains dan Teknik. Volume 1. 7. Ed. Pembelajaran Cengage.
5. Tipler, hlm. (2006). Fisika untuk Sains dan Teknologi. Edisi ke -5. Volume 1. Editorial dikembalikan.