Perbedaan formula, persamaan, contoh, latihan

Itu Perbedaan kubus Itu adalah ekspresi aljabar binomial dari bentuk³ - B³, di mana istilah a dan b dapat berupa bilangan real atau ekspresi aljabar dari berbagai jenis. Contoh perbedaan kubus adalah: 8 - x³, karena 8 dapat ditulis sebagai 2³.

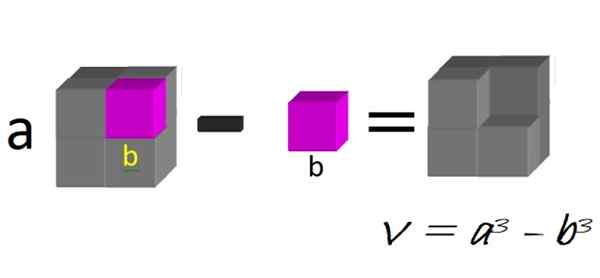
Secara geometris kita dapat memikirkan kubus besar, dari sisi A, di mana bube kecil sisi B dikurangi, seperti yang diilustrasikan dalam Gambar 1:

Gambar 1. Perbedaan kubus. Sumber: f. Zapata.

Volume gambar yang dihasilkan justru perbedaan dalam kubus:

V = a³ - B³

Untuk menemukan ekspresi alternatif, diamati bahwa gambar ini dapat dipecah menjadi tiga prisma, seperti yang ditunjukkan di bawah ini:

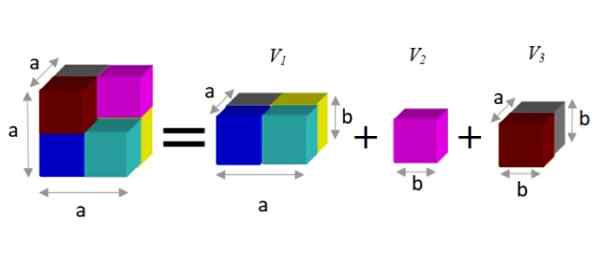Gambar 2. Perbedaan kubus (kiri kesetaraan) sama dengan jumlah volume parsial (kanan). Sumber: f. Zapata.

Prism memiliki volume yang diberikan oleh produk dari tiga dimensinya: lebar x kedalaman x tinggi. Dengan cara ini, volume yang dihasilkan adalah:

V = a³ - B³ = a².b + b³ + ke.B²

Faktor B Itu umum di sebelah kanan. Selain itu, pada gambar yang ditunjukkan di atas dipenuhi secara khusus bahwa:

b = (a/2) ⇒ a = b + b

Oleh karena itu dapat dikatakan bahwa: b = a - b. Dengan demikian:

ke³ - B³ = B (a² + B² +ke.b) = (a-b) (a² + ke.b + b²)

Cara ini mengekspresikan perbedaan dalam kubus akan terbukti sangat berguna dalam banyak aplikasi dan akan diperoleh dengan cara yang sama, meskipun sisi kubus yang hilang di sudut berbeda dari B = A/2.

Perhatikan bahwa tanda kurung keduaItu terlihat sangat besar untuk produk luar biasa dari kuadrat dari jumlah, tetapi istilah yang disilangkan tidak dikalikan dengan 2. Pembaca dapat mengembangkan sisi kanan untuk memverifikasi bahwa itu diperoleh secara efektif ke³ - B³.

[TOC]

Dapat melayani Anda: binomial persegi

Contoh

Ada beberapa perbedaan kubus:

1 - m⁶

ke⁶B³ - 8z¹²Dan⁶

(1/125).X⁶ - 27.Dan⁹

Mari kita analisis masing -masing. Dalam contoh pertama, 1 dapat ditulis sebagai 1 = 1³ dan istilah m⁶ Tetap: (m²)³. Kedua istilah itu adalah kubus yang sempurna, oleh karena itu perbedaannya adalah:

1 -m⁶ = 1³ - (M²)³

Dalam contoh kedua istilah ini ditulis ulang:

ke⁶B³ = (a²B)³

8z¹²Dan⁶ = 2³ (z⁴)³ (Dan²)³ = (2z⁴Dan²)³

Perbedaan kubus ini adalah: (a²B)³ - (2z⁴Dan²)³.

Akhirnya, fraksi (1/125) adalah (1/5³), X⁶ = (x²)³, 27 = 3³ dan dan⁹ = (dan³)³. Mengganti semua ini dalam ekspresi asli, diperoleh:

(1/125).X⁶  - 27y⁹ = [(1/5) (x²)]³ - (3y³)³

Faktorisasi perbedaan kubus

Fakta Perbedaan dalam kubus menyederhanakan banyak operasi aljabar. Untuk melakukan ini, sudah cukup untuk menggunakan rumus yang dikurangi sebelumnya:

Gambar 3. Faktorisasi perbedaan kubus dan ekspresi hasil bagi yang luar biasa. Sumber: f. Zapata.

Sekarang, prosedur untuk menerapkan formula ini terdiri dari tiga langkah:

- Pertama, akar kubik dari masing -masing istilah perbedaan diperoleh.

- Kemudian binomial dan trinomial yang muncul di sisi kanan formula dibangun.

- Akhirnya, binomial dan trinomial diganti untuk mendapatkan faktorisasi akhir.

Kami akan menggambarkan penggunaan langkah -langkah ini dengan masing -masing contoh perbedaan kubus yang diusulkan di atas dan dengan demikian memperoleh setara dengan faktornya.

Contoh 1

Ekspresi Faktif 1 -M⁶   Mengikuti langkah -langkah yang dijelaskan. Kita mulai dengan menulis ulang ekspresi sebagai 1 -m⁶ = 1³ - (M²)³ Untuk mengekstraksi masing -masing akar kubik dari setiap istilah:

Kemudian binomial dan trinomial dibangun:

Itu dapat melayani Anda: teori antrian: sejarah, model, untuk apa dan contohnya

A = 1

b = m²

Jadi:

A - b = 1 - m²

 (ke² +ke.b + b²) = 1² + 1.M² + (M²)² = 1 + m² + M⁴

 Akhirnya diganti dalam formula a³ - B³ = (a-b) (a² +ke.b + b²):

1 -m⁶ = (1 - m²) (1 + m² + M⁴)

Contoh 2

Menguraikan pd pengali:

ke⁶B³ -8z¹²Dan⁶ = (a²B)³ - (2z⁴Dan²)³

Karena ini adalah kubus yang sempurna, akar kubik langsung: a²B dan 2Z⁴Dan², Dari sana, ia mengikuti itu:

- Binomial: a²B - 2Z⁴Dan²

- Trinomial: (a²B)² + ke²B. 2z⁴Dan² + (ke²B +2Z⁴Dan²)²

 Dan sekarang faktorisasi yang diinginkan dibangun:

ke⁶B³ -8z¹²Dan⁶ = (a²B - 2Z⁴Dan²). [(ke²B)² + ke²B. 2z⁴Dan² + (ke²B + 2Z⁴Dan²)²] =

= (a²B - 2Z⁴Dan²). [ke⁴B² + 2nd²B.z⁴Dan² + (ke²B + 2Z⁴Dan²)²]

Pada prinsipnya faktorisasi sudah siap, tetapi seringkali perlu untuk menyederhanakan setiap istilah. Kemudian produk luar biasa dikembangkan dari jumlah - yang muncul di akhir dan kemudian tambahkan istilah yang sama. Mengingat bahwa kuadrat dari jumlah adalah:

(x + y)² = x² + 2xy + dan²

Hak penting atas kanan berkembang dengan cara ini:

(ke²B + 2Z⁴Dan²)² = a⁴B² + 4²B.z⁴Dan² + 4z⁸Dan⁴

 Mengganti perkembangan yang diperoleh dalam faktorisasi perbedaan kubus:

ke⁶B³ -8z¹²Dan⁶ = (a²B - 2Z⁴Dan²). [ke⁴B² + 2nd²B.z⁴Dan² + ke⁴B² + 4²B.z⁴Dan² + 4z⁸Dan⁴] =

Akhirnya, mengelompokkan istilah yang sama dan memperhitungkan koefisien numerik, yang semuanya pasangan, diperoleh:

(ke²B - 2Z⁴Dan²). [2⁴B² + 6²B.z⁴Dan² + 4z⁸Dan⁴] = 2 (a²B - 2Z⁴Dan²). [ke⁴B² + 3²B.z⁴Dan² + 2z⁸Dan⁴]

Contoh 3

Faktorisasi (1/125).X⁶  - 27y⁹ Ini jauh lebih sederhana dari kasus sebelumnya. Pertama setara A dan B diidentifikasi:

A = (1/5) x²

B = 3y³

Kemudian mereka diganti langsung pada formula:

(1/125).X⁶  - 27y⁹ = [(1/5) x² - 3y³]. [(1/25) x⁴ + (3/5) x²Dan³ + 9y⁶]

Olahraga diselesaikan

Perbedaan dalam kubus, seperti yang telah kami katakan, berbagai aplikasi di aljabar. Mari kita lihat beberapa:

Dapat melayani Anda: 5 karakteristik pesawat Cartesian

Latihan 1

Selesaikan persamaan berikut:

a) x⁵ - 125 x² = 0

b) 64 - 729 x³ = 0

Solusi untuk

Pertama persamaannya adalah faktor dengan cara ini:

X² (X³ - 125) = 0

Karena 125 adalah kubus yang sempurna, tanda kurung ditulis sebagai perbedaan dalam kubus:

X² . (X³ - 5³) = 0

Solusi pertama adalah x = 0, tetapi kami menemukan lebih banyak jika kami membuat x³ - 5³ = 0, lalu:

X³ = 5³ → x = 5

Solusi b

Sisi kiri persamaan ditulis ulang sebagai 64 - 729 x³ = 4³ - (9x)³. Karena itu:

4³ - (9x)³ = 0

Karena eksponennya sama:

9x = 4 → x = 9/4

Latihan 2

Ekspresi Faktorisasi:

(x + y)³ - (X - y)³

Larutan

Ekspresi ini adalah perbedaan dalam kubus, jika dalam rumus faktorisasi kita melihat bahwa:

A = x+ dan

b = x- y

Kemudian binomial dibangun terlebih dahulu:

a - b = x+ y - (x- y) = 2y

Dan sekarang trinomial:

ke² + ke.b + b² = (x+ y)² + (x + y) (x-y) + (x-y)²

Produk penting dikembangkan:

(x+ y)² = x² + 2xy +dan²

(x+y) (x-y) = x²- Dan²

(x- y)² = x² - 2xy +dan²

Maka Anda harus mengganti dan mengurangi istilah yang sama:

ke² + ke.b + b² = x² + 2xy +dan²+ X²- Dan²+ X² - 2xy +dan² = 3x² + Dan²

Hasil faktorisasi dalam:

(x + y)³ - (X - y)³ = 2y. (3x² + Dan²)

Referensi

1. Baldor, a. 1974. Aljabar. Editorial Budaya Venezuela S.KE.
2. Yayasan CK-12. Jumlah dan perbedaan kubus. Dipulihkan dari: CK12.org.
3. Akademi Khan. Faktorisasi perbedaan kubus. Pulih dari: is.Khanacademy.org.
4. Matematika itu menyenangkan. Perbedaan dua kubus. Pulih dari: mathsisfun.com
5. Unam. Faktorisasi perbedaan kubus. Diperoleh dari: DCB.Fi-c.Unam.MX.