Perbedaan antara lingkaran dan keliling (dengan contoh)

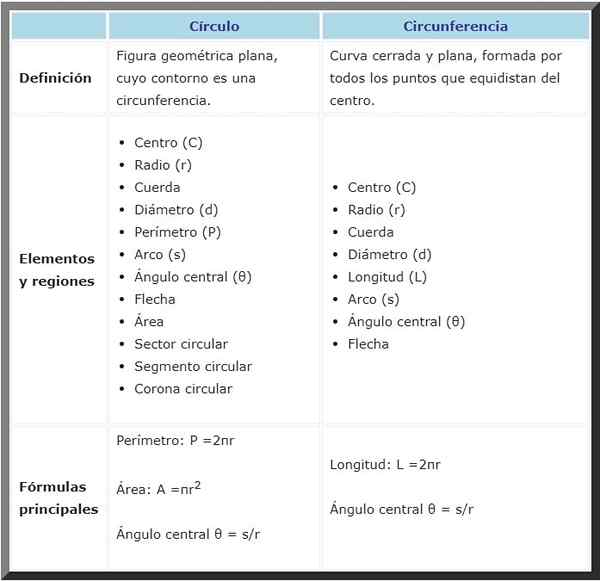
Itu Perbedaan antara lingkaran dan keliling Ini adalah sebagai berikut: Lingkaran adalah permukaan datar, berkontur atau dibatasi oleh lingkaran, sedangkan yang terakhir adalah kurva datar.

Seringkali kedua konsep itu bingung, karena mereka terkait, tetapi Anda harus selalu ingat bahwa keliling adalah tepi lingkaran, sementara itu berisi keliling dan semua titik interiornya.

Keduanya memiliki banyak elemen yang sama, seperti pusat, jari -jari dan diameter, antara lain, menurut tabel komparatif berikut:

	Lingkaran	Lingkar
Definisi	Sosok geometris datar, yang konturnya adalah lingkar.	Kurva tertutup dan datar, dibentuk oleh semua titik yang menjadi Equidist di tengah.
Elemen dan wilayah	Tengah (c) Radio (R) Tali Diameter (d) Perimeter (P) Busur Sudut tengah (Θ) Anak panah Daerah Sektor melingkar Segmen melingkar Mahkota melingkar	Tengah (c) Radio (R) Tali Diameter (d) Panjang (l) Busur Panjang pusat (Θ) Anak panah
Rumus	Perimeter: P = 2π⋅R Area: A =πR2 Sudut Tengah: Θ= s/r	Panjang: l = 2π⋅R Sudut Tengah: Θ= s/r

[TOC]

Lingkaran: definisi, karakteristik dan bagian

Lingkaran adalah sosok geometris datar, yang mencakup semua titik keliling yang membentuk kontur dan juga semua titik interior.

Karena alasan ini ditandai dengan memiliki:

-Tepi atau perimeter, yang merupakan lingkar lingkaran.

-Area yang dangkal.

Elemen lingkaran

Setiap lingkaran memiliki bagian atau elemen berikut:

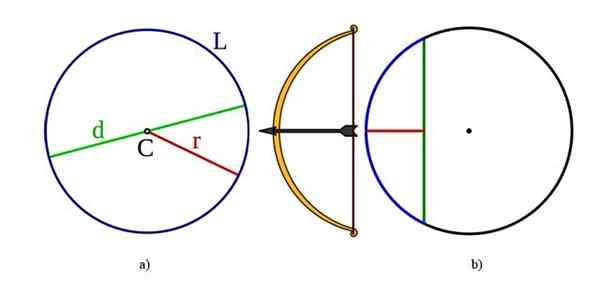Unsur -unsur lingkaran, juga umum untuk keliling: ke kiri di A) adalah pusat D, diameter D, jari -jari R dan panjang l l. Tepat di b) Ada tali dan sagita atau panah. Sumber: Wikimedia Commons.

Tengah: Apa itu titik C, yang Equidists semua titik tepi.

Dapat melayani Anda: busur (geometri): ukuran, jenis lengkungan, contoh

Tali: Segmen yang bergabung dengan dua titik tepi lingkaran. Pada Gambar B) di sebelah kanan, itu adalah segmen hijau yang lebih gelap.

Diameter: segmen hijau yang lebih ringan, dilambangkan "D" pada Gambar A), yang bergabung dengan dua titik tepi dan pada saat yang sama melewati tengah. Diameter juga merupakan tali, yang terpanjang dari semuanya, sehingga dikenal sebagai Tali utama.

Radio: dilambangkan dengan "r" pada Gambar A), itu adalah segmen merah yang bergabung dengan pusat lingkaran dengan titik tepi. Ukurannya setengah diameter.

Busur: Sebagian dari kontur yang ada di antara dua titik ini, dengan warna biru pada Gambar B).

Sudut tengah: Ini adalah sudut yang simpulnya berada di tengah atau dan sisi -sisinya adalah radio lingkaran.

Anak panah: segmen tegak lurus terhadap tali (merah pada Gambar B), yang bergabung dengan pusat tali dengan titik tepi.

Panjang atau perimeter: Ini adalah ukuran kontur lingkaran, dilambangkan l. Itu tergantung pada radio r dan sebanding dengan bilangan irasional π:

π = 3.1416 ..

Sehingga:

L = 2π⋅r

Daerah melingkar

Menjadi sosok datar, lingkaran memiliki area total dan juga berbagai daerah. Yang paling terkenal adalah sebagai berikut:

Area lingkaran: Ini sebanding dengan kuadrat jari -jari, konstanta proporsionalitas adalah angka π.

Memanggil area lingkaran, itu dinyatakan sebagai:

A = πr²

Segmen melingkar: Ini adalah bagian dari lingkaran yang dibatasi oleh busur biru dan tali hijau gelap pada Gambar B.

Dapat melayani Anda: sudut tambahan: apa itu, perhitungan, contoh, latihan

Sektor melingkar: Ini juga merupakan daerah lingkaran, tetapi terkandung antara dua radio dan lengkungan yang sesuai.

Mahkota melingkar: Itu berbentuk seperti cincin dan dibatasi oleh dua keliling konsentris, di luar radio menor dan di dalam walikota radio.

Lingkar: dEfinisi, karakteristik dan bagian 

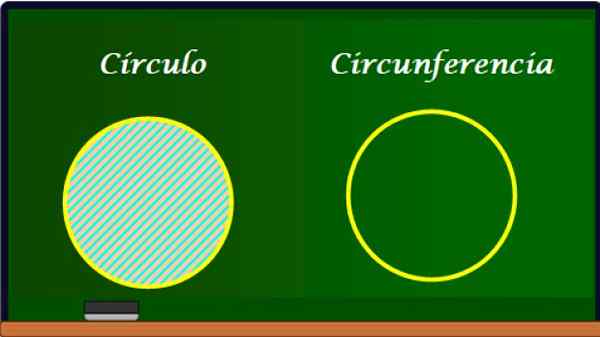Lingkaran dan kelilingnya. Sumber: f. Zapata.

Lingkar adalah tepi lingkaran dan karenanya memiliki banyak elemen yang sama dengan ini. Namun, keliling tidak memiliki area, karena karena itu adalah kurva, ia hanya memiliki panjang l.

Lingkar secara formal didefinisikan sebagai himpunan semua titik yang menyamakan dari titik lain yang dikenal sebagai pusat.

Titik interior tidak termasuk, karena ini sesuai dengan lingkaran.

Elemen keliling

Banyak elemen keliling adalah sama dengan yang dari lingkaran, tidak termasuk yang merujuk pada area dan daerah, sehingga angka atas berfungsi sebagai referensi.

KAMI MEMILIKI:

Tengah: dilambangkan dengan C dan kadang -kadang juga sebagai O, semua titik keliling menjaga jarak yang sama dengannya.

Tali: segmen yang bergabung dengan dua poin milik lingkar.

Diameter: Ini juga bergabung dengan dua titik lingkar, tetapi selalu melewati pusat yang sama.

Radio: Ini adalah jarak antara pusat dan titik lingkaran mana pun.

Busur: Ini adalah bagian dari keliling.

Sudut tengah: Ini adalah sudut dengan titik di tengah C dan dua sisi yang sama yang mengukur seperti radio.

Anak panah: segmen tegak lurus terhadap tali, yang bergabung dengan pusat ini dengan titik keliling yang sesuai.

Dapat melayani Anda: Prinsip Multiplikasi: Teknik dan Contoh Penghitungan

Panjang atau perimeter: Ini adalah ukuran keliling, yang telah kita lihat, sebanding dengan angka π = 3.1416 ... dan dihitung dengan rumus:

L = 2π⋅r

Persamaan keliling

Suatu titik P milik lingkar selama jaraknya ke titik lain C sama dengan R, Radio.

Setiap titik di pesawat Cartesian memiliki koordinat (X, y) dan kuadrat jarak D Di antara mereka berdua, p₁(X₁,Dan₁) Dan p₂(X₂,Dan₂), diberikan oleh formula:

D₂² = (x₂ - X₁)² +  (Dan₂ - Dan₁)²

Mari kita ambil titik koordinat (x, y) dan untuk mengoordinasikan titik C (h, k). Mengganti, persamaan sebelumnya akan seperti ini:

(X - h)² +  (Y- K)² = r²

Ini adalah persamaan keliling, bahwa titik apa pun yang memuaskan. Jika pusat keliling bertepatan dengan asal sistem koordinat, maka h = k = 0 dan persamaan disederhanakan:

X² + Dan² = r²

Mari kita lihat contoh cara menggunakan persamaan dan jawab masalah ini: apakah intinya (4.6) milik lingkar (x - 1)² +  (dan - 2)² = 25?

Untuk mengetahui koordinat titik dalam persamaan diganti, dan jika itu adalah kesetaraan, maka titik tersebut memang milik keliling:

(4 - 1)² +  (6 - 2)² = 3² + 4² = 9 + 16 = 25

Dan memang, seperti 25 = 25, disimpulkan bahwa (4.6) memang milik keliling.

Referensi

1. Tutorial matematika gratis. Area dan perimeter lingkaran - kalkulator geometri. Dipulihkan dari: analisis.com.
2. Referensi Terbuka Matematika. Keliling, perimeter lingkaran. Pulih dari: mathpenref.com.
3. Ilmu pengetahuan. Bagaimana menemukan perimeter lingkaran. Pulih dari: ilmuwan.com.
4. Stewart, J. 2006. PRECCCULMENT: Matematika untuk Perhitungan. Ke -5. Edisi. Pembelajaran Cengage.
5. Zill, d. 1984. Aljabar dan Trigonometri. Bukit McGraw.