Divisi sintetis

Kami menjelaskan apa itu divisi sintetis, metode untuk melakukannya, contoh dan latihan diselesaikan.

Apa itu Divisi Sintetis?

Itu Divisi sintetis Ini adalah cara sederhana untuk membagi P (x) polinomial dengan salah satu bentuk d (x) = x - c - c. Misalnya, polinomial p (x) = (x⁵+3x⁴-7x³+2x²-8x+1) dapat direpresentasikan sebagai penggandaan dua polinomial paling sederhana (x+1) dan (x⁴ + 2x³).

Ini adalah alat yang sangat berguna, karena, selain memungkinkan kita untuk membagi polinomial, juga memungkinkan untuk mengevaluasi polinomial P (x) dalam angka apa pun C, yang pada gilirannya menunjukkan kita secara tepat jika angka itu adalah nol atau tidak dari polinomial.

Berkat algoritma divisi, kita tahu bahwa jika kita memiliki dua P (x) dan d (x) polinomial (x) + r (x), di mana r (x) adalah nol atau kurang dari q (x). Polinomial ini masing -masing dikenal sebagai hasil bagi dan residu atau istirahat.

Pada kesempatan di mana polinomial d (x) adalah dari bentuk x - c, divisi sintetis memberi kita cara singkat untuk menemukan siapa q (x) dan r (x).

Metode Divisi Sintetis

Biarkan p (x) = a_NX^N+ke_N-1X^N-1+... +a₁x+a₀ Polinomial yang ingin kita bagi dan d (x) = x-c the pembagi. Untuk membagi dengan metode divisi sintetis kita melanjutkan sebagai berikut:

1- Kami menulis koefisien p (x) di baris pertama. Jika ada kekuatan x yang tidak muncul, kami menempatkan nol sebagai koefisiennya.

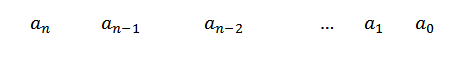
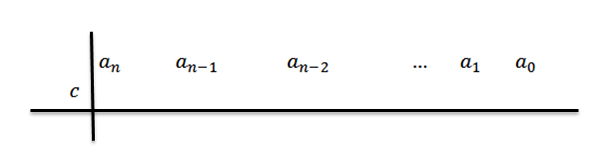
2- Di baris kedua, di sebelah kiri a_N Kami menempatkan C, dan menggambar garis divisi, seperti yang ditunjukkan pada gambar berikut:

3- Kami menurunkan koefisien terkemuka ke baris ketiga.

Dapat melayani Anda: metode euler: apa penggunaan prosedur dan latihan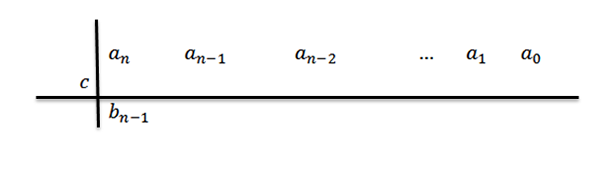

Dalam ungkapan ini b_N-1= a_N

4- Kami mengalikan C dengan koefisien terkemuka b_N-1 Dan kami menulis hasilnya di baris kedua, tetapi kolom di sebelah kanan.

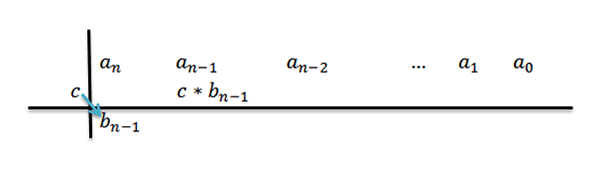
5- Kami menambahkan kolom tempat kami menulis hasil sebelumnya dan hasilnya ditempatkan di bawah jumlah tersebut. Yaitu, di kolom yang sama, baris ketiga.

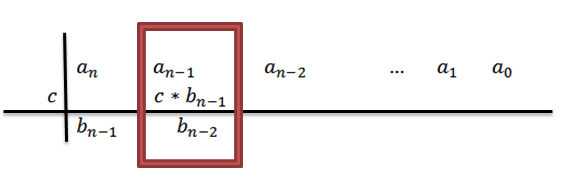
Dengan menambahkan, kami memiliki sebagai hasilnya_N-1+c*b_N-1, yang untuk kenyamanan kita akan menelepon b_N-2

6- Kami mengalikan C dengan hasil sebelumnya dan menulis hasilnya di hak Anda di baris kedua.

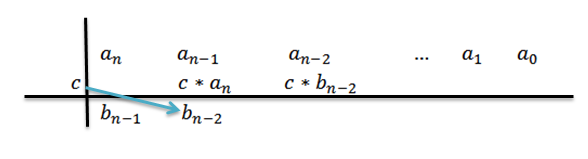
7- Kami ulangi langkah 5 dan 6 sampai kami mencapai koefisien₀.

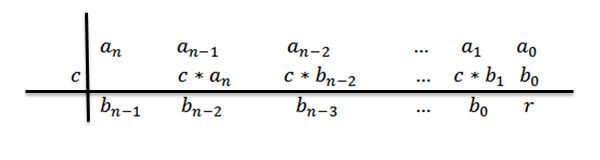
8- Kami menulis jawabannya, yaitu, hasil bagi dan residu. Saat kami melakukan pembagian polinomial grade N antara polinomial grade 1, kami memiliki bahwa hasil bagi akan menjadi grade n-1.

Koefisien polinomial hasil bagi akan menjadi jumlah baris ketiga, kecuali yang terakhir, yang akan menjadi polinomial residu atau sisa divisi.

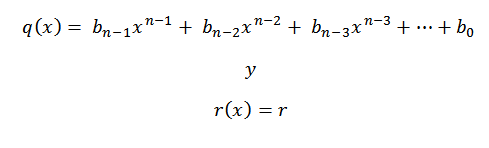
Latihan terpecahkan

Contoh 1

Buat divisi berikut dengan metode divisi sintetis:

(X⁵+3x⁴-7x³+2x²-8x+1): (x+1).

Larutan

Pertama kami menulis koefisien dividen sebagai berikut:

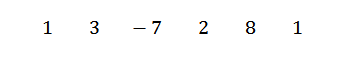
Kemudian kami menulis C di sisi kiri, di baris kedua, bersama dengan garis divisi. Dalam contoh ini c = -1.

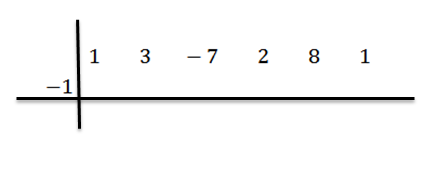
Kami menurunkan koefisien terkemuka (dalam hal ini b_N-1 = 1) dan kami melipatgandakannya dengan -1:

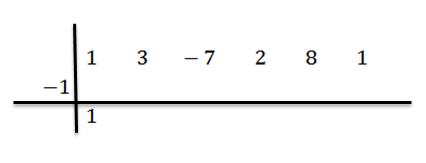
Kami menulis hasilnya di sebelah kanan di baris kedua, seperti yang ditunjukkan di bawah ini:

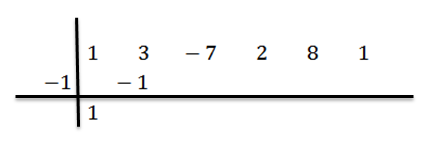
Kami menambahkan nomor kolom kedua:

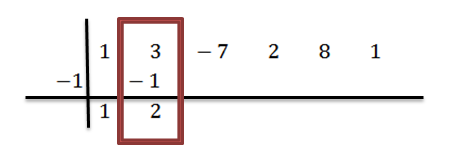
Kami melipatgandakan 2 dengan -1 dan menulis hasilnya di kolom ketiga, baris kedua:

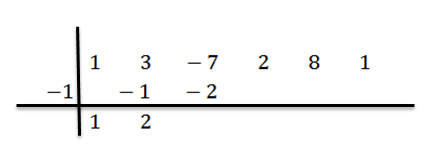
Kami menambahkan kolom ketiga:

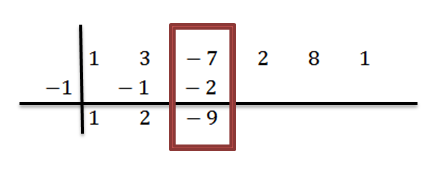
Kami melanjutkan secara analog sampai kami mencapai kolom terakhir:

Dapat melayani Anda: pendekatan default dan kelebihan: apa itu dan contoh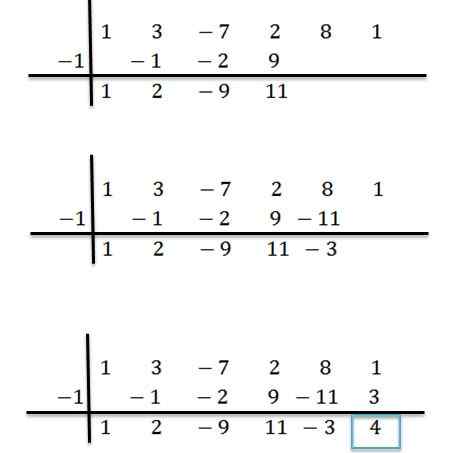

Dengan demikian, kami memiliki bahwa angka terakhir yang diperoleh adalah sisa divisi, dan angka yang tersisa adalah koefisien polinomial yang ada. Ini ditulis sebagai berikut:

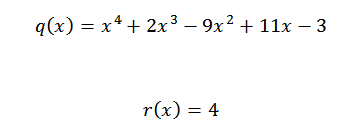
Jika kita ingin memverifikasi bahwa hasilnya benar, itu cukup untuk memverifikasi bahwa persamaan berikut dipenuhi:

P (x) = q (x)*d (x) + r (x)

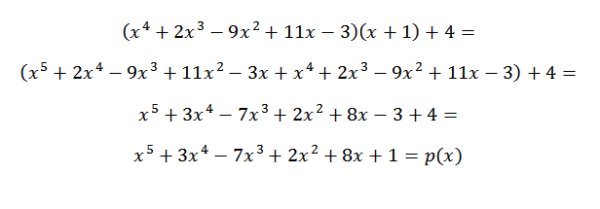
Dengan demikian kita dapat memverifikasi bahwa hasil yang diperoleh sudah benar.

Contoh 2

Lakukan pembagian polinomial berikut dengan metode divisi sintetis:

(7x³-x+2): (x+2)

Larutan

Dalam hal ini kita memiliki istilah x² Itu tidak muncul, jadi kami akan menulis ke 0 sebagai koefisiennya. Dengan demikian, polinomial akan tetap 7x³+0x²-x+2.

Kami menulis koefisien Anda berturut -turut, yaitu:

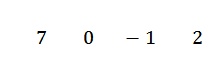
Kami menulis nilai C = -2 ke sisi kiri di baris kedua dan menggambar garis divisi.

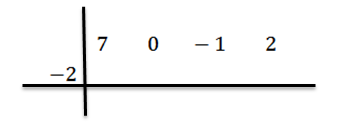
Kami menurunkan koefisien terkemuka b_N-1 = 7 dan kami mengalikannya dengan -2, menulis hasilnya di baris kedua di sebelah kanan.

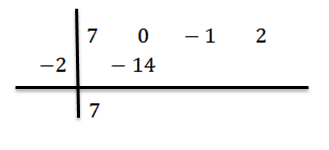
Kami menambahkan dan melanjutkan, seperti yang dijelaskan sebelumnya, sampai kami mencapai istilah terakhir:

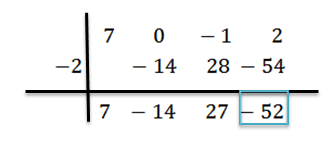
Dalam hal ini, sisanya adalah r (x) = -52 dan hasil bagi yang diperoleh adalah q (x) = 7x²-14x+27.

Contoh 3

Cara lain untuk menggunakan divisi sintetis adalah sebagai berikut.

Untuk algoritma divisi, kita dapat menulis polinomial p (x) sebagai berikut:

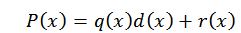
Dalam ungkapan ini, q (x) dan r (x) masing -masing adalah hasil bagi dan sisanya. Sekarang, jika d (x) = x-c, saat mengevaluasi dalam C dalam polinomial kami menemukan yang berikut:

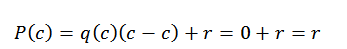
Inilah sebabnya mengapa masih ada untuk menemukan r (x), dan kami dapat melakukan ini berkat divisi sintetis.

Misalnya, kami memiliki polinomial p (x) = x⁷-9x⁶+19x⁵+12x⁴-3x³+19x²-37x-37 dan kami ingin tahu apa nilainya saat mengevaluasinya di x = 5. Untuk ini kami melaksanakan pembagian antara p (x) dan d (x) = x -5 dengan metode divisi sintetis:

Dapat melayani Anda: simetri aksial: sifat, contoh dan latihan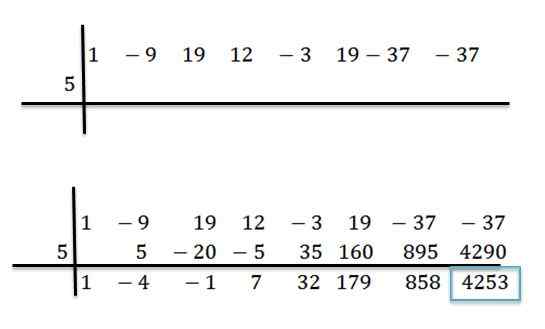

Setelah operasi selesai, kita tahu bahwa kita dapat menulis p (x) sebagai berikut:

P (x) = (x⁶-4x⁵ -X⁴+ 7x³ +32x² +179x + 858)*(x-5) + 4253

Karena itu, saat mengevaluasinya, kita harus:

P (5) = (5-4 (5) -5 +7 (5) +32 (5) +179 (5) +858)*(5-5) +4253

P (5) = (5-4 (5) -5 +7 (5) +32 (5) +179 (5) +858)*(0) +4253

P (5) = 0 + 4253 = 4253

Seperti yang bisa kita lihat, dimungkinkan untuk menggunakan divisi sintetis untuk menemukan nilai polinomial saat mengevaluasinya di C alih -alih hanya mengganti C dengan x. 

Jika kami mencoba mengevaluasi p (5) dengan cara tradisional, kami akan membutuhkan beberapa perhitungan yang biasanya menjadi membosankan.

Contoh 4

Algoritma pembagian untuk polinomial juga dipenuhi untuk polinomial dengan koefisien kompleks dan, sebagai akibatnya, kami memiliki bahwa metode pembagian sintetis juga berfungsi untuk polinomial ini. Selanjutnya, kita akan melihat contohnya.

Kami akan menggunakan metode pembagian sintetis untuk menunjukkan bahwa z = 1+ 2i adalah nol dari P (x) polinomial = x³+ (1+i) x² -(1+2i) x+(15+5i). Yaitu, residu divisi p (x) antara d (x) = x - z sama dengan nol.

Kami melanjutkan seperti sebelumnya: di baris pertama kami menulis koefisien p (x), lalu di yang kedua kami menulis z dan menggambar garis divisi.

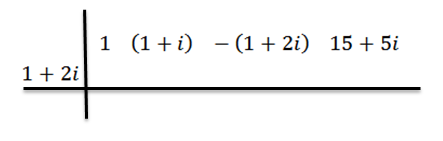
Kami melakukan divisi seperti sebelumnya, yaitu:

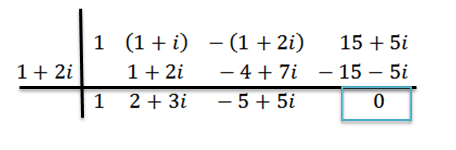
Kita dapat melihat bahwa residu adalah nol; Oleh karena itu, kami menyimpulkan bahwa z = 1+ 2i adalah nol dari p (x).

Referensi

1. Baldor, Aurelio. Aljabar. Grup Editorial Patria.
2. Demana, Waits, Foley & Kennedy. Precáculo: grafik, numerik, aljabar. Pendidikan Pearson.