Persamaan pecahan

Persamaan fraksional termasuk fraksi numerik dan/atau aljabar, dan yang tidak diketahui mungkin ada dalam pembilang dan penyebut, atau keduanya

Apa persamaan fraksional?

Itu Persamaan pecahan adalah mereka yang mengandung pecahan dalam satu atau lebih persyaratan mereka. Fraksi seperti itu dapat berupa numerik atau aljabar, di mana yang tidak diketahui dapat ditemukan di pembilang dan/atau dalam penyebut dari istilah apa pun.

Kemudian, beberapa contoh persamaan fraksional dengan satu yang tidak diketahui:

Contoh pertama adalah persamaan linier dengan koefisien fraksional; Dalam contoh kedua, yang tidak diketahui adalah dalam denominator masing -masing istilah, dan yang terakhir, yang tidak diketahui adalah pembilang dan dalam penyebut.

Untuk menyelesaikannya, perlu melakukan beberapa transformasi aljabar dan dengan demikian memperoleh persamaan yang setara, di mana yang tidak diketahui tidak muncul dalam penyebut. Setelah prosedur ini dilakukan, solusinya ditemukan menggunakan teknik yang sesuai.

Solusinya terdiri dari himpunan nilai "x" yang memenuhi kesetaraan. Ini bisa menjadi nilai yang unik, atau beberapa, tetapi, dalam hal apa pun, sangat penting untuk diingat bahwa tidak semua solusi dalam persamaan yang setara dapat diterima oleh persamaan asli.

Memang, jika itu adalah persamaan yang tidak diketahui dalam denominator, nilai "X" yang membatalkannya harus dihindari, bahkan jika mereka termasuk dalam himpunan solusi persamaan yang setara. Ini karena pembagian antara 0 tidak ditentukan.

Jika persamaan yang setara memiliki solusi unik, dan ternyata penyebut dari salah satu ketentuan persamaan asli dibatalkan, maka ia tidak memiliki solusi.

Cara memecahkan persamaan fraksional

Operasi yang dilakukan untuk menyelesaikan persamaan non -fraksional valid, asalkan kesetaraan dipertahankan. Dengan cara ini, dalam persamaan fraksional Anda dapat menambahkan atau mengurangi jumlah yang sama ke kedua sisi kesetaraan, melipatgandakan semua istilah dengan jumlah yang sama, atau membagi setiap istilah dengan jumlah yang sama (berbeda dari 0).

Dapat melayani Anda: Teorema Bolzano

Tetapi karena persamaan fraksional diperlukan untuk berubah menjadi setara lain tanpa denominator, indikasi umum berikut juga diikuti:

1. Temukan kelipatan umum minimum dari denominator (m.C.M).
2. Lipat gandakan setiap istilah dengan m.C.M., Untuk menghilangkan penyebut.
3. Menyelesaikan persamaan yang setara yang diperoleh.
4. Pastikan bahwa solusi yang ditemukan memenuhi kesetaraan asli.

Jenis persamaan yang setara

Persamaan yang setara yang diperoleh mengikuti prosedur yang ditunjukkan dapat:

• Linear atau tingkat pertama
• Kuadrat
• Orde yang lebih tinggi

Contoh terpecahkan

Contoh 1

Selesaikan persamaan berikut:

Perlu dicatat bahwa persamaan adalah derajat pertama dalam "x", karena "x" tinggi pada 1. Koefisien persamaan adalah fraksi dan cara untuk menghilangkannya, untuk bekerja dengan bilangan bulat, itu mengalikan semua istilah dengan kelipatan minimum penyebut (m.C.M.).

M.C.M. (2,3,6) = 6

Jadi:

3x - 2x = 1

x = 1

Pembaca dapat memeriksa validitas solusi ini, mengganti x = 1 dalam persamaan asli dan memverifikasi bahwa kesetaraan diperoleh.

Contoh 2

Tentukan nilai "x" yang memuaskan:

Berbeda dengan contoh sebelumnya, dalam hal ini tidak diketahui ditemukan dalam penyebut. Perhatikan bahwa penyebut dibatalkan karena nilai x = 2 dan x = −1, detail yang lebih mudah dipertimbangkan, karena, jika persamaan yang setara mengakui solusi ini, kita harus membuangnya, karena mereka tidak dapat diterima Dalam persamaan asli.

Sekarang kita harus mengubah persamaan menjadi orang lain tanpa penyebut, langkah pertama adalah membuat jumlah istilah di sebelah kiri kesetaraan:

Karena penyebutnya sama, sehingga kesetaraan terpenuhi, perlu bahwa pembilang juga:

Dapat melayani Anda: Proporsionalitas Konstanta: Apa itu, Perhitungan, Latihan

4 (x+1) - 3 (x -2) = 8

Cukup untuk menyelesaikan persamaan ini, yang ternyata kelas satu:

4x + 4 - 3x + 6 = 8

x = 8 - 6 - 4 = - 2

x = - 2

Karena nilai ini berbeda dari nilai yang dilarang, itu diakui sebagai solusi dari persamaan asli.

Contoh 3

Temukan solusi dari:

Dalam persamaan ini, nilai x = 4 membatalkan penyebut, oleh karena itu, dikeluarkan dari set solusi persamaan yang diubah, jika muncul.

Persamaan yang diubah mudah ditemukan, cukup untuk melipatgandakan semua istilah dengan faktor (X-4):

Tetap:

2x - 4 = 4

2x = 8

x = 4

Contoh 4

Selesaikan persamaan:

Dalam hal ini, penyebut memiliki istilah kuadratik, sehingga lebih mudah untuk memperhitungkan mereka terlebih dahulu:

• X² + 8x + 7 = (x + 7) (x + 1)
• X² - 49 = (x + 7) (x - 7)
• X² - 6x - 7 = (x - 7) (x + 1)

Persamaannya seperti ini:

Nilai x yang membatalkan salah satu penyebut adalah: x = −7, x = 7, x = −1. Oleh karena itu, bahkan jika nilai -nilai ini adalah bagian dari set solusi dari persamaan yang dimodifikasi, mereka tidak dapat menjadi solusi dari persamaan asli.

Sekarang datang proses mengubah persamaan. Langkah pertama adalah menemukan kelipatan umum minimum dari denominator:

M.C.M. = (x + 7) (x - 7) (x + 1)

Dengan mengalikan kedua sisi kesetaraan dengan m.C.M. tersisa:

Yang dihasilkan:

(x --7) (x− 2) = (x + 1) (2x - 5) - (x + 7) (x - 2)

Melalui properti distributif produk dikembangkan:

X² - 9x +14 = 2x² - 3x - 5 - (x² + 5x - 14)

Mengurangi istilah serupa di sisi kanan:

X² - 9x + 14 = x² - 8x + 9

Istilah kuadrat dibatalkan, dengan memenuhi tanda yang sama di sisi kesetaraan yang berbeda:

Dapat melayani Anda: Perbedaan kubus: Rumus, persamaan, contoh, latihan

- 9x + 14 = - 8x + 9

-x = -5 ⇒ x = 5

Hasil ini diakui sebagai solusi, karena bukan nilai yang dilarang.

Latihan aplikasi persamaan fraksional

Penyebut fraksi melebihi empat unit untuk pembilang. Jika pembilang dikurangi dari pembilang dan penyebut juga, fraksi yang dihasilkan adalah 3/5. Tentukan fraksi asli.

Larutan

Biarkan x menjadi nilai pembilang.

Karena penyebut fraksi melebihi empat unit ke pembilang, fraksi asli adalah:

Sekarang Anda harus mengurangi 5 unit, baik untuk pembilang dan penyebut:

Karena fraksi yang dihasilkan dari melaksanakan prosedur sebelumnya sama dengan 3/5, mereka disamakan:

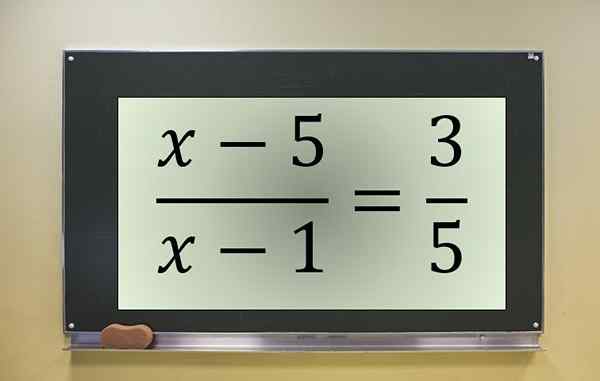Contoh Persamaan Fraksional. Sumber: f. Zapata.

Ini adalah persamaan fraksional dengan yang tidak diketahui dalam pembilang dan penyebut, yang dibatalkan pada x = 1. Oleh karena itu, nilai ini harus dikecualikan, jika itu adalah salah satu solusi dari persamaan yang diubah.

Kemudian, ia melipatgandakan kedua sisi dengan kelipatan umum minimum, yaitu 5 (x - 1):

Menghasilkan persamaan yang setara berikut:

5 (x - 5) = 3 (x - 1)

Menerapkan properti distributif:

5x -25 = 3x - 3 ⇒ 2x = 22

x = 11

Fraksi asli menggantikan x = 11 dalam ekspresi:

Menghasilkan fraksi 11/15. Ini adalah jawaban untuk masalah yang diangkat.

Referensi

1. Persamaan pecahan. Dipulihkan dari: Mathepower.com
2. Portal Matematika. Persamaan pecahan. Resolusi masalah. Pulih dari: silvioduarte.com.
3. Stewart, J. (2007). PRECCCULMENT: Matematika untuk Perhitungan. Ke -5. Edisi. Pembelajaran Cengage.
4. Sullivan, m. (1997). Prekalkulasi. 4. Edisi. Pendidikan Pearson.
5. Zill, d. (2008). Prekcculment dengan kemajuan perhitungan. 4. Edisi. Bukit McGraw.