Dalam situasi apa fungsi linier dan kuadrat?

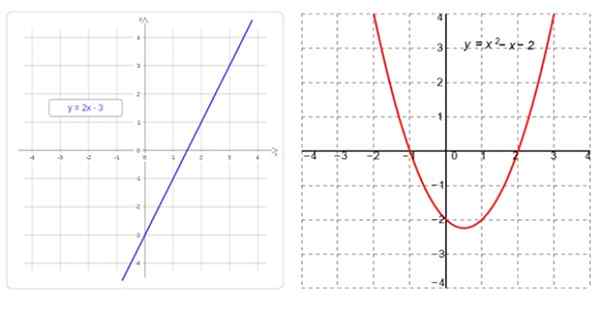
Di sebelah kiri fungsi linier, yang grafiknya adalah garis lurus, dan di sebelah kanan, fungsi kuadratik, yang grafiknya adalah parabola. Sumber: f. Zapata

Apa fungsi linier dan kuadratik?

Fungsi linier dan fungsi kuadrat adalah fungsi yang termasuk dalam kelompok fungsi polinomis. Mereka digunakan untuk memodelkan berbagai situasi, seperti ketergantungan antara volume dan berat badan, jumlah dan biaya suatu produk, posisi versus waktu dan banyak lagi.

Secara umum, fungsi adalah hubungan yang menghubungkan dua variabel dan dapat digunakan untuk memodelkan dunia nyata. Fungsi polinomik, seperti namanya, diekspresikan melalui polinomial, yang bentuk umumnya adalah:

f (x) = a_NX^N + ke _N-1X ^N-1 + ke_X-2X^N-2 +… ke_{salah satu}

Di mana n adalah angka alami, angka untuk₀, ke₁, ke₂,… ke_N Mereka nyata, untuk₀ Itu adalah istilah independen dan untuk_N, Itu adalah koefisien yang menyertai daya tertinggi. Nilai n menunjukkan jenis fungsi, untuk n = 1 fungsi linier, sedangkan untuk n = 2 fungsinya adalah kuadratik.

Dalam kasus pertama ini, ekspresi umum dikurangi menjadi:

f (x) = a₁x + a_{salah satu}

Dan dalam kasus kedua, tetap seperti ini:

f (x) = a₂X² + ke₁x + a_{salah satu} ;   (ke₂≠ 0)

Grafik fungsi polinomial terus menerus, yaitu, mereka tidak mengalami lompatan atau pecah secara tiba -tiba, sehingga memiliki perilaku lembut, tanpa penyimpangan. Oleh karena itu, mereka diamati dalam pemodelan banyak situasi sains, ekonomi dan bidang pengetahuan manusia lainnya.

Selanjutnya, aplikasi yang menarik satu sama lain dijelaskan secara lebih rinci.

Situasi di mana fungsi linier muncul

Fungsi linier diwakili secara aljabar dengan:

f (x) = a₁x + a_{salah satu}

Atau setara:

f (x) = mx + b

Fitur khasnya adalah grafiknya adalah garis lurus. Nilai M, yang merupakan koefisien dari X, mewakili subang dari garis ini dan memberikan ukuran seberapa cenderung itu.

Dapat melayani Anda: pemrograman non -linier: metode dan latihan

Kemiringan bisa positif, negatif atau nol, tetapi selalu konstan, yaitu, nilai tukarnya tetap tidak berubah.

Garis kemiringan 0 benar -benar horizontal, yaitu kemiringan positif menunjukkan peningkatan atau peningkatan (jika salah satu variabel meningkat, yang lain juga, selalu pada tingkat yang sama) dan, akhirnya, kemiringan negatif menunjukkan penurunan (sebagai variabel dari variabel meningkat, yang lainnya berkurang).

Nilai dari B, Untuk bagiannya, itu mewakili potongan atau persimpangan garis dengan sumbu vertikal. Ya B = 0, Garis melewati asal sistem koordinat.

Contoh pemodelan dengan fungsi linier

1. Gerakan Burkas Lembaga Seragam

Persamaan yang menghubungkan posisi x dan waktu t ponsel, dalam gerakan bubur seragam, adalah linier:

x (t) = v⋅t + x_{salah satu}

Di mana V, kemiringan garis, adalah kecepatan ponsel, yang tetap konstan di seluruh gerakan, dan x_{salah satu} adalah posisi awal.

2. Kepadatan

Kepadatan suatu objek atau zat, yang menetapkan hubungan antara massa dan volume. Memanggil ρ ke kepadatan (berbunyi "rho"), m ke adonan dan v ke volume, Anda memiliki:

Membersihkan adonan, dalam hal volume, diperoleh:

M = ρv

Saat memberi grafik adonan tergantung pada volume, garis lurus diperoleh yang kemiringannya adalah kepadatan objek atau zat.

3. Panjang lingkar

Kontur lingkaran, atau panjangnya, sebanding dengan radius. Ini berarti bahwa semakin besar jari -jari, semakin besar kontur lingkar, sesuai dengan persamaan:

Dapat melayani Anda: Koefisien Korelasi: Rumus, Perhitungan, Interpretasi, Contoh

C = 2πr

Di mana c adalah kontur atau panjang, r adalah radio dan π (membaca "pi") adalah konstanta yang nilainya perkiraannya πamp3.14 ..

4. Biaya pengiriman paket

Karena mudah disimpulkan, yang lebih berat atau tebal adalah paket yang lebih mahal adalah mengangkutnya. Perusahaan yang berdedikasi untuk model transportasi kargo harga mengikuti aturan tertentu, misalnya:

C (x) = 2.75x

Dalam persamaan ini, C (x) adalah biaya dolar untuk mengirim paket yang beratnya adalah x pound. Nilai konstan 2.75 memiliki unit dolar/pound (biaya unit).

Situasi di mana fungsi kuadratik muncul

Secara aljabar, fungsi kuadratik diwakili oleh:

f (x) = a₂ X² + ke₁ x + a_{salah satu}

Dengan kondisi yang koefisien₂ Berbeda dari 0. Ini ditandai dengan grafik berbentuk parabola, yang sumbu aksial atau sumbu simetri vertikal (sejajar dengan sumbu y)).

Persimpangan antara perumpamaan dan sumbu tersebut adalah titik yang disebut vertex. Jika perumpamaan terbuka (a₂ > 0), simpul adalah titik minimumnya, dan jika dibuka ke bawah (a₂ < 0), es el máximo.

Pada sumbu simetri adalah fokus, titik khusus yang menentukan kelengkungan parabola. Jika sinar matahari dipengaruhi pada cermin parabola, sinar akan tercermin di permukaan, bertepatan dalam fokus, yang segera dipanaskan.

Contoh pemodelan dengan fungsi kuadratik

1. Tinggi proyektil yang diluncurkan secara vertikal

Proyektil adalah objek apa pun yang disediakan kecepatan awal dan kemudian dirilis, di bawah aksi gravitasi. Jika kecepatan awal vertikal, besarnya v₀ dan diarahkan, objek akan naik ke ketinggian maksimum dan kemudian turun.

Dapat melayani Anda: homotecia

Persamaan tinggi h sebagai fungsi waktu t adalah:

H (t) = −4.9 t²+v₀ T

Di mana indera vertikal dianggap positif, dan vertikal turun negatif.

2. Lintasan proyektil horizontal atau miring

Jika kecepatan awal horizontal atau miring disediakan untuk proyektil, itu akan menggambarkan lintasan parabola, yang dapat diwakili melalui fungsi kuadratik seperti yang dijelaskan sebelumnya.

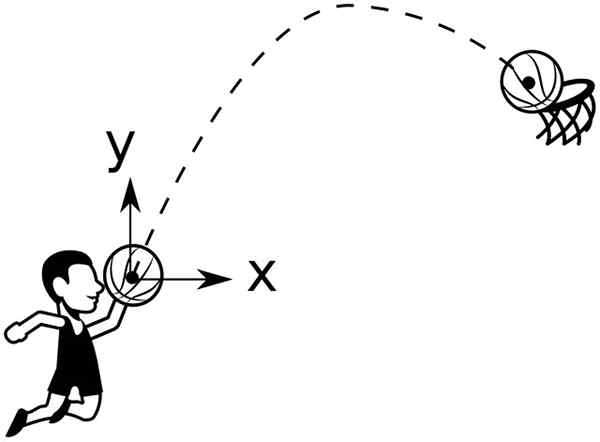Bola keranjang menggambarkan lintasan parabola untuk dilemparkan ke dalam keranjang. Sumber: Wikimedia Commons

Misalnya, bola yang dilemparkan dari ketinggian dan₀, membentuk sudut θ₀ Mengenai horizontal, ia memiliki lintasan yang diberikan oleh:

Dengan g sebagai percepatan gravitasi, yang dapat mendekati 10 m/s². Misalnya, tendangan bola sepak dari tanah (dan₀ = 0), dengan kecepatan awal 6 m/s dan sudut 45º sehubungan dengan horizontal, akan memiliki lintasan yang diberikan oleh perumpamaan berikut:

3. Area lingkaran

Semakin tinggi jari -jari lingkaran, semakin besar luasnya. Memang, area lingkaran sebanding dengan kuadrat jari -jari R, konstanta proporsionalitas adalah jumlah π:

A = πr²

4. Efektivitas iklan

Semakin banyak mereka melihatnya, semakin efektif iklan komersial. Efektivitas E, pada skala dari 0 hingga 10, dari satu pemberitahuan dapat dimodelkan sesuai dengan fungsi kuadratik berikut:

Referensi 

1. Fungsi polinomik. Dipulihkan dari sumber daya.pendidikan.adalah.
2. Larson, r. (2012). Prekalkulasi. Ke -8. edisi. Pembelajaran Cengage.
3. Miller, c. (2013). Matematika: Penalaran dan Aplikasi. 12. edisi. Pendidikan Pearson.
4. Stewart, J. (2012). Prekalkulasi. Matematika untuk perhitungan. 6. edisi. Pembelajaran Cengage.
5. Zill, d. (2008). Prekcculment dengan kemajuan perhitungan. 4. edisi. Bukit McGraw.