Ruang vektor dasar dan dimensi, aksioma, sifat

A ruang vektor Itu adalah set yang tidak bagus V= atau, v, W,…, elemen siapa yang vektor. Dengan mereka beberapa operasi penting dilakukan, di antaranya yang berikut ini menonjol:

- Jumlah antara dua vektor u + v sebagai akibat z, yang menjadi milik keseluruhan V.

- Multiplikasi bilangan real α dengan vektor v: α v yang memberi vektor lain Dan yang termasuk dalam V.

Visi artistik ruang vektor. Sumber: Pixabay

Untuk menunjukkan vektor, kami menggunakan huruf tebal (v Itu adalah vektor), dan untuk skalar atau angka huruf Yunani (α adalah angka).

[TOC]

Aksioma dan sifat

Untuk menjadi ruang vektor, delapan aksioma berikutnya harus dipenuhi:

1-Konmutabilitas: atau +v = v +atau

2-transitifitas: (atau + v) + W = atau + ( v + W)

3-eksistensi vektor nol 0 seperti yang 0 + v = v

4-keberadaan yang sebaliknya: kebalikan dari v adalah (-v) , mengingat bahwa v + (-v) = 0

Distribusi 5-produk sehubungan dengan jumlah vektor: α ( atau + v ) = αatau +αv

Distributivitas 6-produk sehubungan dengan jumlah skalar: (α + β)v = αv +βv

7-asosiasi produk skalar: α (β v) = (α β)v

8-the Number 1 Itu adalah elemen netral sejak: 1v = v

Contoh ruang vektor

Contoh 1

Vektor di pesawat (R²) adalah contoh ruang vektor. Vektor dalam bidang adalah objek geometris yang memiliki besarnya dan arah. Itu diwakili oleh segmen berorientasi yang dimiliki pesawat tersebut dan dengan ukuran yang sebanding dengan besarnya.

Jumlah dua vektor dalam bidang dapat didefinisikan sebagai operasi geometris vektor kedua setelah yang pertama. Hasil dari jumlahnya adalah segmen berorientasi yang dimulai dari asal yang pertama dan mencapai ujung yang kedua.

Pada gambar dapat dicatat bahwa jumlah dalam r² adalah komutatif.

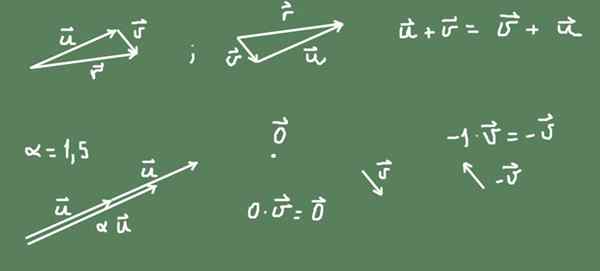Gambar 2. Vektor di bidang membentuk ruang vektor. Sumber: Made sendiri.

Produk dari angka α juga ditentukan oleh vektor. Jika angkanya positif, alamat vektor asli dipertahankan dan ukurannya α kali vektor asli. Jika angkanya negatif, alamatnya sebaliknya, dan ukuran vektor yang dihasilkan adalah nilai absolut dari angka.

Vektor menentang vektor apapun v adalah -v = (-1) v.

Vektor nol adalah titik dalam bidang r², dan angka nol dengan vektor menghasilkan vektor nol.

Semua dikatakan diilustrasikan pada Gambar 2.

Contoh 2

Mengatur P Dari semua polinomial kurang dari atau sama dengan dua, termasuk tingkat nol, mereka membentuk set yang memenuhi semua aksioma ruang vektor.

Itu dapat melayani Anda: acara yang saling eksklusif: properti dan contoh

Jadilah polinomial p (x) = a x² + b x + c y q (x) = d x² + e x + f

Jumlah dua polinomial didefinisikan: p (x) + q (x) = (a + d) x² + (b + e) ​​x + (c + f)

Jumlah polinomial milik keseluruhan P Itu komutatif dan transitif.

Polinomial nol milik keseluruhan P Ini adalah salah satu yang memiliki semua koefisiennya sama dengan nol:

0 (x) = 0 x² + 0 x + 0

Jumlah skalar α ditentukan oleh polinomial seperti: α p (x) = α ∙ a x² + α ∙ b x + α ∙ c

Polinomial yang berlawanan dari p (x) adalah -p (x) = (-1) p (x).

Dari semua hal di atas itu mengikuti set itu P Dari semua polinomial kurang dari atau sama dengan dua, itu adalah ruang vektor.

Contoh 3

Mengatur M Dari semua matriks dari baris M x n kolom yang elemennya adalah bilangan real membentuk ruang vektor nyata, sehubungan dengan jumlah matriks dan produk angka dengan matriks.

Contoh 4

Set F fungsi kontinu dari variabel nyata, membentuk ruang vektor, karena jumlah dua fungsi dapat didefinisikan, multiplikasi skalar dengan fungsi, fungsi nol dan fungsi simetris. Mereka juga memenuhi aksioma yang menjadi ciri ruang vektor.

Dasar dan dimensi ruang vektor

Basis

Satu set vektor independen linier didefinisikan sebagai dasar ruang vektor sedemikian rupa sehingga dari kombinasi linier dari mereka vektor ruang vektor tersebut dapat dihasilkan.

Secara linear menggabungkan dua atau lebih vektor terdiri dari mengalikan vektor dengan skalar dan kemudian menambahkannya secara vektor.

Misalnya, dalam ruang vektor vektor dalam tiga dimensi yang dibentuk oleh R³ basis kanonik yang ditentukan oleh unit vektor (magnitudo 1) digunakan (magnitudo 1) yo, J, k.

Di mana yo = (1, 0, 0); J = (0, 1, 0); k = (0, 0, 1). Ini adalah vektor kartesia atau kanonik.

Vektor apa pun V milik r³ ditulis sebagai V = a yo + B J + C k, yang merupakan kombinasi linier dari vektor dasar yo, J, k. Skalar atau angka a, b, c dikenal sebagai komponen cartesian dari V.

Dikatakan juga bahwa vektor dasar ruang vektor membentuk satu set ruang vektor.

Dimensi

Dimensi ruang vektor adalah jumlah kardinal dari basis vektor untuk ruang tersebut; yaitu, jumlah vektor yang membentuk basis tersebut.

Kardinal ini adalah jumlah maksimum vektor independen linier dari ruang vektor itu, dan pada saat yang sama jumlah minimum vektor yang membentuk set penghasil ruang tersebut.

Dapat melayani Anda: Populasi Statistik: Konsep, Jenis, Contoh

Basis ruang vektor tidak unik, tetapi semua pangkalan ruang vektor yang sama memiliki dimensi yang sama.

Subruang vektor

Subruang vektor dari ruang vektor V adalah subset dari V di mana operasi yang sama didefinisikan seperti dalam V dan memenuhi semua aksioma ruang vektor. Oleh karena itu, subruang juga akan menjadi ruang vektor.

Contoh subruang vektor adalah vektor milik bidang xy. Subruang ini adalah subset dari ruang vektor dimensi yang lebih besar dari himpunan vektor milik ruang tiga -dimensi xyz.

Contoh lain dari subspace vektor S1 dari ruang vektor dibentuk oleh semua matriks 2 × 2 dengan elemen nyata adalah yang ditentukan di bawah ini:

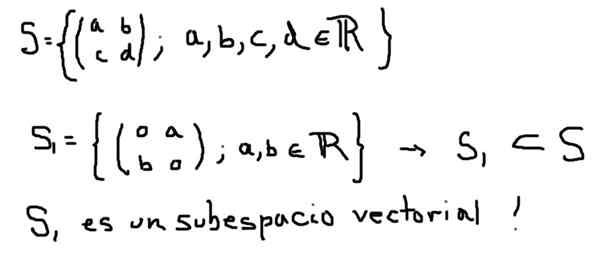
Di sisi lain, S2 yang didefinisikan di bawah ini, meskipun merupakan subset dari S, itu tidak membentuk subruang vektor:

Latihan terpecahkan

-Latihan 1

Jadilah vektor V1= (1, 1, 0); V2= (0, 2, 1) dan V3= (0, 0, 3) dalam r³.

a) Buktikan bahwa mereka secara linear mandiri.

b) Buktikan bahwa mereka membentuk basis di R³, karena daftar apa pun (x, y, z) dapat ditulis sebagai kombinasi linier dari V1, V2, V3.

c) Temukan komponen daftar V = (-3,5,4) di pangkalan V1, V2, V3.

Larutan

Kriteria untuk menunjukkan independensi linier adalah untuk menetapkan serangkaian persamaan berikut dalam α, β dan γ

α (1, 1, 0) + β (0, 2, 1) + γ (0, 0, 3) = (0, 0, 0)

Jika satu -satunya solusi untuk sistem ini adalah α = β = γ = 0 maka vektor secara linear independen, jika tidak mereka tidak.

Untuk mencapai nilai α, β dan γ kami mengusulkan sistem persamaan berikut:

α ∙ 1 + β ∙ 0 + γ ∙ 0 = 0

α ∙ 1 + β ∙ 2 + γ ∙ 0 = 0

α ∙ 0 + β ∙ 1 + γ ∙ 3 = 0

Yang pertama mengarah ke α = 0, α kedua = -2 ∙ β tetapi sebagai α = 0 lalu β = 0. Persamaan ketiga menyiratkan bahwa γ = (-1/3) β, tetapi sebagai β = 0 lalu γ = 0.

Menjawab

Disimpulkan bahwa itu adalah seperangkat vektor independen linier di R³ .

Jawaban b

Sekarang mari kita tulis daftar (x, y, z) sebagai kombinasi linier dari v1, v2, v3.

(x, y, z) = α v1 + β v2 + γ v3 = α (1, 1, 0) + β (0, 2, 1) + γ (0, 0, 3)

α ∙ 1 + β ∙ 0 + γ ∙ 0 = x

α ∙ 1 + β ∙ 2 + γ ∙ 0 = y

Itu dapat melayani Anda: Tukey Test: Apa yang, dalam kasus contoh, latihan terpecahkan

α ∙ 0 + β ∙ 1 + γ ∙ 3 = z

Dimana Anda memiliki:

α = x

α + 2 β = y

β + 3 γ = z

Yang pertama menunjukkan α = x, β = (y-x)/2 kedua dan γ = ketiga (z- y/2 +x/2)/3. Dengan cara ini kami telah menemukan generator α, β dan γ dari daftar r³ 

Jawaban c

Mari kita temukan komponen daftar V = (-3,5,4) di pangkalan V1, V2, V3.

Kami mengganti nilai yang sesuai dalam ekspresi yang ditemukan di atas untuk generator.

Dalam hal ini kita memiliki: α = -3; β = (5-(-3))/2 = 4; γ = (4- 5/2 +(- 3)/2)/3 = 0

Itu adalah:

(-3,5,4) = -3 (1, 1, 0) + 4 (0, 2, 1) + 0 (0, 0, 3)

Akhirnya:

V = -3 V1 + 4 V2 + 0 V3

Kami menyimpulkan itu V1, v2, v3 Mereka membentuk basis di ruang vektor r³ dimensi 3.

-Latihan 2

Ekspres polinomial p (t) = t² + 4t -3 sebagai kombinasi linier p1 (t) = t² -2t + 5, p2 (t) = 2t² -3t dan p3 (t) = t + 3.

Larutan

P (t) = x p1 (t) + dan p2 (t) + z p3 (t)

dimana angka x, y, z harus ditentukan.

Dengan mengalikan dan pengelompokan istilah dengan gelar yang sama di T itu diperoleh:

T² + 4 t -3 = (x + 2y) t² + (-2x -3y + z) t + (5x + 3z)

Yang membawa kita ke sistem persamaan berikut:

x + 2y = 1

-2x -3y + z = 4

5x + 3z = -3

Solusi dari sistem persamaan ini adalah:

x = -3, y = 2, z = 4.

Itu adalah:

P (t) = -3 p1 (t) + 2 p2 (t) + 4 p3 (t)

-Latihan 3

Tunjukkan vektor itu V1= (1, 0, -1, 2); V2= (1, 1, 0, 1) dan V3= (2, 1, -1, 1) dari R⁴ secara linear independen.

Larutan

Kami secara linear menggabungkan tiga vektor V1, V2, V3 Dan kami menuntut kombinasi menambahkan elemen nol r⁴

ke V1 + B V2 + C V3 = 0

Artinya,

A (1, 0, -1, 2) + B (1, 1, 0, 1) + C (2, 1, -1, 1) = (0, 0, 0, 0)

Ini membawa kita ke sistem persamaan berikut:

A + B + 2 C = 0

B + C = 0

-A - C = 0

2 A + B + C = 0

Mengurangi yang pertama dan keempat yang kita miliki: -a + c = 0 apa yang menyiratkan a = c.

Tetapi jika kita melihat persamaan ketiga, kita harus = -c. Satu-satunya cara untuk memenuhi a = c = (-c) adalah bahwa C adalah 0 dan karenanya juga akan 0.

A = c = 0

Jika kami mengganti hasil ini dalam persamaan pertama maka kami menyimpulkan bahwa b = 0.

Akhirnya A = B = C = 0, sehingga dapat disimpulkan bahwa vektor V1, V2 dan V3 secara linear independen.

Referensi

1. Lipschutz, s. 1993. Aljabar linier. Edisi kedua. McGraw - Hill. 167 - 198.