Karakteristik faktor umum, contoh, latihan

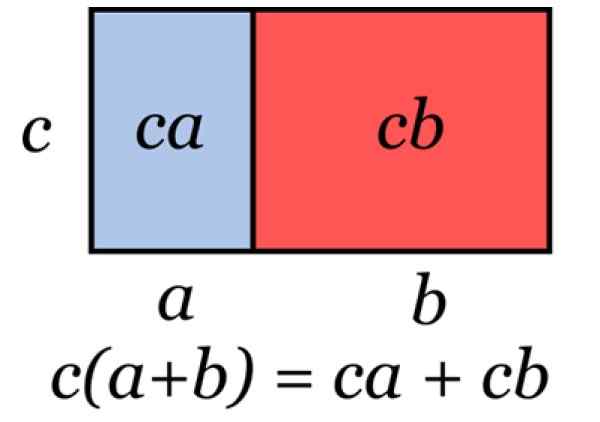
Dia faktor umum ekspresi aljabar adalah jumlah yang ada dalam semua hal ini. Ketika faktor umum diketahui, dimungkinkan untuk menulis ekspresi dengan cara yang setara melalui produk faktor.

Tidak semua ekspresi aljabar memiliki faktor umum, hanya ada yang hanya dapat dibagi di antara mereka dan 1, oleh karena itu tidak mungkin untuk menulisnya sebagai produk dari faktor. Contoh ekspresi yang tidak memiliki faktor umum adalah:

x + y

Gambar 1. Faktor umum dari ekspresi aljabar membuatnya menjadi produk yang ditunjukkan dari dua faktor. Sumber: Pixabay.

Sebaliknya ini ya:

5a + 10b

Terlihat bahwa 5 hadir dalam kedua istilah, karena 10 = 5 ∙ 2. Karena 5 adalah faktor umum, maka berikut ini dapat ditulis:

5a + 10b = 5 ∙ (a + 2b)

Pembaca dapat memeriksa melalui properti distributif, bahwa ekspresi di sebelah kanan sama dengan aslinya.

Faktor umum juga bisa literal atau kombinasi angka dan huruf, misalnya 4x² - 2x. Itu X dan 2 Mereka berada di antara faktor -faktor dan ekspresi tetap sebagai produk:

4x² -2x = 2x⋅ (x --1)

Keuntungan menemukan faktor umum dari suatu ekspresi dan menulisnya sebagai produk adalah hampir selalu mudah untuk beroperasi dengannya. Itulah sebabnya digunakan dalam banyak prosedur aljabar dan perhitungan seperti:

-Saat memecahkan persamaan, yang solusinya dengan cepat terungkap ketika faktor umum ditemukan.

-Saat menghitung batas dengan ketidakpastian, ini mungkin hilang dengan memperhitungkan dengan benar.

-Faktorisasi yang tepat juga memfasilitasi operasi dengan ekspresi aljabar rasional, seperti jumlah dan pengurangan.

[TOC]

Karakteristik faktor umum

Karakteristik utama dari faktor umum adalah sebagai berikut:

-Ini bisa berupa angka, ekspresi aljabar, atau kombinasi keduanya.

-Faktor umum harus terkandung dalam masing -masing istilah ekspresi ke faktor.

Dapat melayani Anda: Fungsi Transenden: Jenis, Definisi, Properti, Contoh

-Menurut jumlah istilah yang dikandungnya, itu mungkin terjadi:

1. Faktor monomial umum, jika faktor umum adalah dari satu istilah tunggal,
2. Faktor binomial umum jika Anda memiliki dua istilah dan
3. Faktor polinomial umum, jika faktor umum terdiri dari beberapa istilah.

Bagaimana menemukan faktor umum dari ekspresi aljabar?

Untuk menemukan faktor umum yang ada dalam polinomial, Anda harus menghitung pembagi umum maksimum atau MCD dari koefisien numerik dari semua istilah, serta huruf atau literal dari setiap istilah dan pilih kekuatan dengan eksponen sekecil apa pun sedikit pun.

Surat atau literal dapat disajikan sebagai monomial, binomial atau polinomial, seperti yang akan dilihat dalam contoh -contoh berikut.

Yang paling disarankan untuk memahami proses mendapatkan faktor umum, adalah mengikuti contoh dan praktik memecahkan beberapa latihan dalam setiap kasus.

Contoh faktor umum

Kita tidak boleh melupakan fakta bahwa tujuan faktor umum dikonversi ekspresi menjadi produk yang ditunjukkan dari faktor -faktor. Maka kasus yang paling relevan dianalisis:

Faktor monomial umum

Anda memiliki monomial berikut (ekspresi aljabar termah tunggal):

2x²; 10x⁴Dan; 100x⁶Dan²

Apa yang bisa menjadi faktor umum untuk ketiganya?

Dimulai dengan koefisien numerik: 2, 10 dan 100, semuanya bahkan dan MCD mereka 2. Adapun bagian literal, variabel X hadir dalam tiga istilah, dan daya terendah adalah x², Maka faktor umumnya adalah 2x².

Tiga istilah yang diusulkan dapat ditulis sebagai produk dari faktor ini dengan cara ini:

2x²= 2x²∙ 1

10x⁴y = 2x² ∙ 5x²Dan

100x⁶Dan²= 2x²∙ 50x⁴Dan²

Mengalikan faktor -faktor di sebelah kanan, dapat diverifikasi bahwa istilah kiri diperoleh.

Gambar 2. Ilustrasi yang mewakili faktor umum. Sumber: Wikimedia Commons.

Teknik ini diterapkan ketika diperlukan untuk memperhitungkan ekspresi aljabar, seperti dalam contoh -contoh berikut:

• Contoh 1

Faktanya ungkapan berikut:

Itu bisa melayani Anda: Segitiga Isosceles

5x³dan + 10x²Dan² + 5xy²

MCD dari koefisien numerik dari setiap istilah adalah:

MCD (5.10) = 5

Adapun bagian literal, keduanya X sebagai Dan Mereka hadir dalam tiga istilah dan eksponen paling sedikit dari masing -masing adalah 1, oleh karena itu faktor umum adalah 5xy Dan Anda bisa menulis:

5x³dan + 10x²Dan² + 5xy²= 5xy ∙ (x² +2xy²+Dan)

Faktor polinomial umum

Faktor umum dapat terdiri dari binomial, trinomial atau secara umum dalam polinomial. Dalam hal ini, instruksi di bagian sebelumnya masih valid, memilih sebagai faktor umum yang satu dengan eksponen sekecil apa pun.

• Contoh 2

Tulis ekspresi berikut sebagai produk dari dua faktor:

2a (x - 1) - 3b (x --1)

Dengan inspeksi langsung, faktor umum adalah binomial (X-1), Jadi:

2a (x - 1) - 3b (x - 1) = (x -1) ∙ (2a - 3b)

Faktorisasi dengan mengelompokkan istilah

Terkadang keberadaan faktor umum tidak jelas, tetapi terungkap jika istilah dikelompokkan dengan cara yang nyaman:

• Contoh 3

Faktorisasi 3x³ - 9ax² - x + 3a

Sekilas tidak ada faktor umum dalam empat istilah ini, karena misalnya X Ini hadir di tiga yang pertama, tetapi tidak di akhir. Dan ke Itu adalah yang kedua dan yang terakhir tidak lebih.

Adapun koefisien, ada tiga istilah di mana 3 hadir, namun menjadi faktor umum, itu harus dalam semua istilah.

Tampaknya teknik yang dijelaskan tidak dapat diterapkan kali ini. Namun, ekspresi dapat memperhitungkan dengan mengelompokkan dua istilah pertama dan dua terakhir, berhati -hati saat menempatkan tanda kurung, bahwa tanda -tanda itu tepat untuk tidak mengubah aslinya:

Dapat melayani Anda: komponen persegi panjang dari vektor (dengan latihan)

3x³ - 9ax² - x + 3a = (3x³ - 9ax²) - (x - 3a)

Perhatikan tanda negatif di tengah tanda kurung: itu perlu, karena jika tidak, ekspresi asli akan berubah.

Dalam tanda kurung kiri faktor umum 3x², Karena itu:

(3x³ - 9ax²) - (x - 3a) = 3x²⋅ (x - 3a) - (x - 3a)

Dan diamati bahwa faktor umum telah muncul: (x - 3a), Artinya, itu adalah faktor untuk kedua kalinya untuk mendapatkan:

3x² (X- 3a) - (x - 3a) = (x - 3a) ∙ ( 3x²- 1)

Latihan Faktor Umum

Latihan 1

Selesaikan persamaan 4x³ +7x²  +6x = 0

Larutan

"X" adalah faktor umum, oleh karena itu:

3x³ −5x²  +2x = x (3x² −5x +2) = 0

Untuk ekspresi di sebelah kiri, itu adalah 0, sudah cukup bahwa salah satu dari dua kondisi ini dipenuhi:

x = 0

SALAH SATU:

3x² −5x +2 = 0

Ini adalah persamaan tingkat kedua lengkap yang dapat diselesaikan dengan menerapkan rumus umum, juga dengan menggunakan kalkulator ilmiah atau metode aljabar lainnya. Solusi dari persamaan ini adalah:

x = 1

x = 2/3

Setelah ditemukan, ini adalah ilustratif untuk menulis persamaan sebagai produk dari 3 faktor, meskipun pernyataan itu tidak memintanya. Itu akan seperti ini:

x⋅ (x-1) ⋅ (x-2/3) = 0

Latihan 2

Hitung batas berikut jika ada:

Larutan

Pertama diganti pada x = −2 untuk mencoba mengevaluasi batas, dengan melakukan itu diperoleh:

Karena ini merupakan ketidakpastian dari bentuk 0/0, Anda harus menjadi faktor untuk mencoba menghilangkannya. Penyebut tidak bisa menjadi faktor, tetapi pembilang tidak.

Dalam pembilang faktor umum adalah X:

X²+2x = x ∙ (x+2)

Ekspresi faktorisasi diganti dalam batas dan dengan cara ini ketidakpastian menghilang:

Disimpulkan bahwa batas ada dan bernilai −2.

Referensi

1. Baldor, a. 2005. Aljabar. Kelompok tanah air budaya.
2. Jiménez, r. 2008. Aljabar. Prentice Hall.
3. Larson, r. 2012. Prekalkulasi. Ke -8. Edisi. Pembelajaran Cengage.
4. Stewart, J. 2007. PRECCCULMENT: Matematika untuk Perhitungan. Ke -5. Edisi. Pembelajaran Cengage.
5. Zill, d. 1984. Aljabar dan Trigonometri. Bukit McGraw.