Faktor Umum untuk Pengelompokan Contoh Ketentuan, Latihan

Dia Faktor Umum untuk Pengelompokan Ketentuan Ini adalah prosedur aljabar yang memungkinkan penulisan beberapa ekspresi aljabar dalam bentuk faktor. Untuk mencapai tujuan ini, ekspresi harus terlebih dahulu mengelompokkan dan mengamati bahwa masing -masing kelompok yang terbentuk, pada dasarnya, memiliki faktor umum.

Menerapkan teknik dengan benar membutuhkan beberapa latihan, tetapi dalam waktu singkat dimungkinkan untuk mendominasi. Mari kita lihat terlebih dahulu contoh ilustratif yang dijelaskan langkah demi langkah. Kemudian pembaca dapat menerapkan apa yang mereka pelajari di setiap latihan yang akan muncul setelahnya.

Gambar 1. Hapus Faktor Umum Untuk Pengelompokan Istilah Memfasilitasi Pekerjaan dengan Ekspresi Aljabar. Sumber: Pixabay.

Misalnya, misalkan Anda perlu memperhitungkan ekspresi berikut:

2x² + 2XY - 3ZX - 3ZY

Ekspresi aljabar ini terdiri dari 4 monomial atau istilah, dipisahkan oleh tanda -tanda + dan -, yaitu:

2x², 2xy, -3zx, -3zy

Mengamati dengan hati -hati, X adalah umum untuk tiga yang pertama, tetapi tidak ke yang terakhir, sedangkan dan umum untuk yang kedua dan keempat, dan z adalah umum untuk yang ketiga dan keempat.

Jadi pada prinsipnya tidak ada faktor umum untuk empat istilah pada saat yang sama, tetapi jika mereka dikelompokkan karena akan ditampilkan di bagian berikut, orang dapat membantu menulis ekspresi sebagai produk dari dua atau lebih faktor.

[TOC]

Contoh

Faktor ekspresi: 2x² + 2XY - 3ZX - 3ZY

Langkah 1: Kelompok

2x² + 2XY - 3ZX - 3ZY = (2x² + 2xy) + (-3zx - 3zy)

Langkah 2: Hapus faktor umum dari masing -masing kelompok

2x² + 2XY - 3ZX - 3ZY =

= (2x² + 2xy) - (3zx + 3zy) =

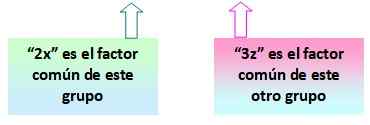
= 2x (x+y) - 3z (x+y)

yoMPORTANTE: Tanda negatif juga merupakan faktor umum yang harus diperhitungkan.

Dapat melayani Anda: ruang vektor: basis dan dimensi, aksioma, properti

Sekarang perhatikan bahwa tanda kurung (x+y) diulang dalam dua istilah yang diperoleh saat pengelompokan. Itulah faktor umum yang dicari.

Langkah 3: Faktorisasi semua ekspresi

2x² + 2XY - 3ZX - 3ZY = (x+y) (2x - 3z)

Dengan hasil sebelumnya, tujuan faktorisasi telah tercapai, yang tidak lain adalah mengubah ekspresi aljabar berdasarkan jumlah dan pengurangan istilah, dalam produk dari dua atau lebih faktor, dalam contoh kami, dari: (x+ y) dan (2x - 3z).

Masalah penting tentang faktor kelompok umum

pertanyaan 1: Bagaimana mengetahui bahwa hasilnya benar?

Menjawab: Properti distributif diterapkan pada hasil yang diperoleh dan setelah mengurangi dan menyederhanakan, ekspresi yang dicapai harus bertepatan dengan yang asli, jika tidak, ada kesalahan.

Dalam contoh sebelumnya, ia bekerja terbalik dengan hasilnya, untuk memverifikasi bahwa itu baik -baik saja:

(x+y) (2x - 3z) = 2x² -3zx +2xy - 3zy

Karena urutan addends tidak mengubah jumlah, setelah menerapkan properti distributif, semua persyaratan asli, ada tanda -tanda yang disertakan, oleh karena itu, faktorisasi itu benar.

Pertanyaan 2: Bisakah Anda mengelompokkan dengan cara lain?

Menjawab: Ada ekspresi aljabar yang mengakui lebih dari satu bentuk pengelompokan dan lainnya yang tidak. Dalam contoh yang dipilih, pembaca dapat mencoba kemungkinan lain, misalnya pengelompokan:

2x² + 2XY - 3ZX - 3ZY = (2x²- 3zx) + (2xy - 3zy)

Dan Anda dapat melihat bahwa hasilnya sama dengan yang diperoleh di sini. Menemukan kelompok yang optimal adalah masalah latihan.

Dapat melayani Anda: Demieve Cotangent: Perhitungan, Demonstrasi, Latihan

Pertanyaan 3: Mengapa perlu untuk mendapatkan faktor umum dari ekspresi aljabar?

Menjawab: Karena ada aplikasi di mana ekspresi faktorisasi memfasilitasi perhitungan. Misalnya, misalkan Anda ingin melakukan 2x² + 2XY - 3ZX - 3ZY sama dengan 0. Apa yang akan menjadi kemungkinan?

Untuk menanggapi masalah ini, versi faktorisasi jauh lebih berguna daripada pengembangan asli dalam hal. Itu muncul seperti ini:

(x+y) (2x - 3z) = 0

Satu kemungkinan bahwa ekspresi bernilai 0 adalah x = -y, terlepas dari nilai z. Dan yang lainnya adalah x = (3/2) z, tanpa masalah nilai y.

Latihan

- Latihan 1

Dapatkan faktor umum dari ekspresi berikut dengan mengelompokkan istilah:

kapak+ay+bx+oleh

Larutan

Dua yang pertama dikelompokkan, dengan faktor umum "A" dan dua yang terakhir dengan faktor umum "B":

AX+AY+BX+oleh = A (x+y)+B (x+y)

Setelah ini selesai, faktor umum baru terungkap, yaitu (x+y), sehingga:

AX+AY+BX+oleh = A (x+y)+b (x+y) = (x+y) (a+b)

Cara lain untuk mengelompokkan

Ekspresi ini mengakui cara pengelompokan lain. Mari kita lihat apa yang terjadi jika istilah itu diatur ulang dan grup dibuat dengan mana mereka berisi X dan lainnya dengan yang mengandung dan:

AX +AY +BX +BY = AX +BX +AY +BY = X (A +B) +Y (A +B)

Dengan cara ini faktor umum baru adalah (A+B):

AX+AY+BX+BY = AX+BX+AY+BY = X (A+B)+Y (A+B) = (x+y) (A+B)

Yang mengarah pada hasil yang sama dari cara pengelompokan pertama yang diuji.

- Latihan 2

Diperlukan untuk menulis ekspresi aljabar berikut sebagai produk dua faktor:

3³ - 3²B+9AB²-ke²+AB-3B²

Dapat melayani Anda: Coplanares Points: Persamaan, Contoh, dan Latihan Terpecahkan

Larutan

Ekspresi ini berisi 6 istilah. Mari kita coba pengelompokan pertama dan keempat, kedua dan ketiga dan akhirnya kelima dan keenam:

3³ - 3²B+9AB²-ke²+AB-3B² = (3³ -ke²) + (- 3²B+9AB²) + (AB-3B²)

Sekarang setiap tanda kurung adalah faktor:

= (3³ -ke²) + (- 3²B+9AB²) + (Ab -3b²) = a² (3a -1) + 3ab (3b -a) + b (a -3b)

Sekilas tampaknya situasinya rumit, tetapi pembaca tidak boleh berkecil hati, karena kita akan menulis ulang istilah terakhir:

ke² (3a -1) + 3ab (3b -a) + b (a -3b) = a² (3a - 1) + 3ab (3b -a) - b (3b -a)

Dua istilah terakhir sekarang memiliki faktor umum, yaitu (3B-A), sehingga mereka dapat diperkuat. Sangat penting untuk tidak melupakan masa jabatan pertama² (3a - 1), yang harus terus menemani segalanya sebagai menambahkan, jadi Anda tidak bekerja dengannya:

ke² (3a - 1) + 3ab (3b -a) - b (3b -a) = a² (3a-1) + (3b-a) (3ab-b)

Ekspresi telah dikurangi menjadi dua istilah dan faktor umum baru ditemukan di yang terakhir, yaitu "B". Sekarang tetap:

ke² (3a-1) + (3b-a) (3ab-b) = a² (3a-1) +b (3b-a) (3a-1)

Faktor umum berikutnya dalam tampil adalah 3 - 1:

ke² (3a - 1) +b (3b -a) (3a -1) = (3a - 1) [a² + B (3B-A)]

Atau jika Anda lebih suka tanpa tanda kurung persegi:

(3 - 1) [a² + B (3b -a)] = (3a - 1) (a² -AB + 3B²)

Dapatkah pembaca menemukan cara lain pengelompokan yang mengarah pada hasil yang sama ini?

Gambar 2. Latihan faktorisasi yang diusulkan. Sumber: f. Zapata.

Referensi

1. Baldor, a. 1974. Aljabar Dasar. Budaya Venezuela S.KE.
2. Jiménez, r. 2008. Aljabar. Prentice Hall.
3. Kasus Faktorisasi Utama. Pulih dari: julioprofe.bersih.
4. Unam. Matematika Dasar: Faktorisasi dengan Mengelompokkan istilah. Fakultas Akuntansi dan Administrasi.
5. Zill, d. 1984. Aljabar dan Trigonometri. Bukit MacGraw.