Aliran volumetrik

Kami menjelaskan apa itu aliran volumetrik, bagaimana menghitungnya dan faktor -faktor yang mempengaruhi itu

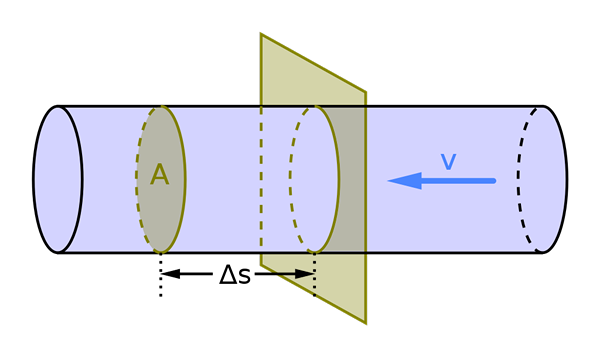
Aliran volumetrik tergantung pada luas penampang A dan kecepatan fluida v. Sumber: Mikerun, CC BY-SA 4.0, via Wikimedia Commons

Apa itu aliran volumetrik?

Dia Aliran volumetrik Ini memungkinkan untuk menentukan volume cairan yang melintasi bagian saluran dan menawarkan ukuran kecepatan yang digunakan cairan dengan hal yang sama. Oleh karena itu, ukurannya sangat menarik di bidang yang beragam seperti industri, kedokteran, konstruksi dan penelitian, antara lain.

Namun, mengukur kecepatan cairan (baik cairan, gas atau campuran keduanya) tidak sesederhana kecepatan perpindahan tubuh padat untuk mengukur. Oleh karena itu, kebetulan mengetahui kecepatan cairan yang perlu diketahui alirannya.

Dari ini dan banyak masalah lain yang terkait dengan cairan, cabang fisika yang dikenal sebagai penawaran mekanika fluida. Aliran didefinisikan sebagai bagaimana cairan bagian dari saluran terjadi, sudah merupakan pipa, pipa, sungai, saluran, aliran darah, dll., dengan mempertimbangkan unit sementara.

Biasanya volume bahwa area tertentu dalam satuan waktu dihitung, juga disebut aliran volumetrik. Aliran massa atau massa yang melintasi area yang ditentukan pada waktu tertentu juga didefinisikan, meskipun lebih jarang digunakan daripada aliran volumetrik.

Bagaimana aliran volumetrik dihitung?

Aliran volumetrik diwakili oleh huruf q. Untuk kasus -kasus di mana aliran bergerak secara tegak lurus ke bagian pengemudi, ditentukan dengan rumus berikut:

Q = a = v / t

Dalam Formula A ini A itu adalah bagian pengemudi (ini adalah kecepatan rata -rata yang dimiliki cairan), V adalah volume dan waktu T. Karena dalam sistem internasional area atau bagian pengemudi diukur dalam m² Dan kecepatan dalam m/s, aliran diukur m³/S.

Dapat melayani Anda: 21 acara penting fisika

Untuk kasus di mana kecepatan perpindahan cairan menciptakan sudut θ dengan arah tegak lurus terhadap bagian permukaan A, ekspresi untuk menentukan aliran adalah sebagai berikut:

Q = a cos θ

Ini konsisten dengan persamaan sebelumnya, karena ketika aliran tegak lurus terhadap area A, θ = 0 dan, oleh karena itu, cos θ = 1.

Persamaan di atas hanya benar jika kecepatan fluida seragam dan jika bagian bagiannya datar. Jika tidak, aliran volumetrik dihitung melalui integral berikut:

Q = ∫∫_S V D S

Dalam DS integral ini adalah vektor permukaan, ditentukan oleh ekspresi berikut:

Ds = n ds

Di sana, N adalah vektor unit normal ke permukaan saluran dan DS elemen permukaan diferensial.

Persamaan kontinuitas

Karakteristik cairan yang tidak dapat dimampatkan adalah bahwa massa cairan diawetkan dengan menggunakan dua bagian. Inilah sebabnya mengapa persamaan kontinuitas terpenuhi, yang menetapkan hubungan berikut:

ρ₁ KE₁ V₁ = ρ₂ KE₂ V₂

Dalam persamaan ini ρ adalah kepadatan cairan.

Untuk kasus -kasus rezim dalam aliran permanen, di mana kepadatannya konstan dan, oleh karena itu, dipenuhi bahwa ρ₁ = ρ₂, Itu dikurangi menjadi ekspresi berikut:

KE₁ V₁ = A₂ V₂

Ini setara dengan menegaskan bahwa aliran dipertahankan dan, oleh karena itu: karena itu:

Q₁ = Q₂.

Dari pengamatan di atas, maka cairan itu meningkat ketika mereka mencapai bagian saluran yang lebih sempit, sementara mereka mengurangi kecepatan mereka ketika mereka mencapai bagian saluran yang lebih luas. Fakta ini memiliki aplikasi praktis yang menarik, karena memungkinkan untuk bermain dengan kecepatan perpindahan cairan.

Dapat melayani Anda: partikel subatomik

Prinsip Bernoulli

Prinsip Bernoulli menentukan bahwa untuk cairan yang ideal (yaitu, cairan yang tidak memiliki viskositas atau gesekan) yang bergerak dalam rezim sirkulasi melalui saluran tertutup terpenuhi bahwa energinya tetap konstan di seluruh perpindahannya.

Pada akhirnya, prinsip Bernoulli tidak lain adalah perumusan hukum konservasi energi untuk aliran cairan. Dengan demikian, persamaan Bernoulli dapat diformulasikan sebagai berikut:

H +v² / 2g+p/ ρg = konstan

Dalam persamaan ini h adalah tinggi dan g adalah percepatan gravitasi.

Dalam persamaan Bernoulli energi cairan diperhitungkan kapan saja, energi yang terdiri dari tiga komponen.

• Komponen kinetik yang mencakup energi, karena kecepatan cairan bergerak.
• Komponen yang dihasilkan oleh potensi gravitasi, sebagai konsekuensi dari ketinggian di mana cairan berada.
• Komponen energi aliran, yang merupakan energi yang dimiliki cairan karena tekanan.

Dalam hal ini, persamaan Bernoulli dinyatakan sebagai berikut:

H ρ g +(v² ρ)/2 + p = konstan

Secara logis, dalam kasus cairan nyata ekspresi persamaan Bernoulli tidak terpenuhi, karena dalam perpindahan cairan ada kerugian gesekan dan perlu untuk menggunakan persamaan yang lebih kompleks.

Apa yang mempengaruhi aliran volumetrik?

Aliran volumetrik akan terpengaruh jika ada obstruksi di saluran.

Dapat melayani Anda: refraksi ringan: elemen, hukum dan percobaan

Selain itu, aliran volumetrik juga dapat berubah dengan mempengaruhi suhu suhu dan variasi tekanan dan tekanan yang menjadi.

Metode sederhana untuk mengukur aliran volumetrik

Metode yang sangat sederhana untuk mengukur aliran volumetrik adalah membiarkan aliran fluida dalam tangki pengukuran untuk periode waktu tertentu.

Metode ini umumnya tidak terlalu praktis, tetapi kebenarannya adalah bahwa itu sangat sederhana dan sangat ilustratif untuk memahami makna dan pentingnya mengetahui aliran cairan.

Dengan cara ini, cairan dibiarkan mengalir ke tangki pengukuran untuk jangka waktu tertentu, volume akumulasi diukur dan hasil yang diperoleh antara waktu yang berlalu dibagi.

Referensi

1. Aliran (cairan) (n.D.).  Di Wikipedia. Pulih dari es.Wikipedia.org.
2. Laju aliran volumetrik (n.D.).  Di Wikipedia. Diterima dari.Wikipedia.org.
3. Engineers Edge, LLC. "Persamaan laju aliran volumetrik fluida". Insinyur tepi
4. Mott, Robert (1996). "1". Mekanika Cairan Terapan (Edisi ke -4). Meksiko: Pendidikan Pearson.
5. Batchelor, g.K. (1967). Pengantar Dinamika Fluida. Cambridge University Press.
6. Landau, l.D.; Lifshitz, e.M. (1987). Mekanika Cairan. Kursus Fisika Teoritis (edisi ke -2.). Pergamon Press.