Koefisien gesekan (gaya) kental dan contoh

Itu gesekan kental Itu muncul ketika benda padat bergerak di tengah gas -un gas atau cairan-. Itu dapat dimodelkan sebagai kekuatan yang sebanding dengan negatif dari kecepatan objek atau kuadrat.

Penggunaan satu atau model lain tergantung pada kondisi tertentu, seperti jenis fluida di mana objek dipindahkan dan apakah itu sangat cepat atau tidak. Model pertama dikenal sebagai Resistensi linier, dan di dalamnya besarnya gesekan kental f_menyentuh Itu diberikan oleh:

F_menyentuh = ΓV

Gambar 1. Paracharidists mengalami kekuatan kental selama keturunan mereka, karena udara menawarkan perlawanan. Sumber: Pixabay.

Di sini γ adalah konstanta proporsionalitas atau koefisien gesekan kental dan V adalah kecepatan objek. Ini berlaku untuk badan yang bergerak dengan kecepatan cairan rendah dengan rezim laminar.

Dalam model kedua, dikenal sebagai Resistensi kuadratik o Hukum Rayleight, besarnya gaya gesekan dihitung menurut:

F_menyentuh = ½ ρ.KE.C_D.v²

Di mana ρ adalah kepadatan cairan, a adalah luas silang -ectional dari objek dan c_D Itu adalah koefisien resistensi aerodinamis.

Produk ½ ρ.KE.C_D  Ini adalah aerodinamika konstan yang disebut D, yang unitnya adalah kg/m, oleh karena itu: oleh karena itu:

F_menyentuh = Dv²

Model ini lebih tepat ketika kecepatan objek sedang atau tinggi, karena gerakan menghasilkan turbulensi atau berputar di jalurnya dalam cairan.

Bola tenis yang bergerak dan mobil -mobil di jalan raya adalah contoh objek di mana model ini bekerja dengan cukup baik.

Gaya viscose muncul karena padatan harus mengambil lapisan cairan untuk dapat bergerak melewatinya. Keberadaan beberapa model adalah karena gaya ini tergantung pada beberapa faktor, seperti viskositas fluida, kecepatan dan bentuk objek.

Dapat melayani Anda: apa itu permeabilitas relatif?

Ada lebih banyak objek aerodinamis daripada yang lain dan banyak yang dirancang tepat sehingga resistensi tengah mengurangi kecepatannya seminimal mungkin.

[TOC]

Contoh gesekan viscose

Setiap orang atau objek yang bergerak dalam cairan tentu mengalami ketahanan dari lingkungan, tetapi berkali -kali efek ini dibenci untuk aplikasi sederhana seperti jatuh bebas.

Dalam pernyataan hampir semua masalah jatuh bebas, tercatat bahwa efek resistensi udara membenci diri sendiri. Ini karena udara adalah cairan yang agak "tipis" dan itulah sebabnya kami berharap gesekan yang ditawarkannya tidak signifikan.

Tetapi ada gerakan lain di mana gesekan kental memiliki pengaruh yang lebih menentukan, mari kita lihat beberapa contoh:

Batu yang jatuh ke dalam air dan biji -bijian serbuk sari

-Batu yang jatuh secara vertikal ke dalam tabung yang penuh dengan oli mengalami kekuatan yang menentang keturunannya, berkat ketahanan fluida.

-Butir serbuk sari sangat kecil, jadi bagi mereka perlawanan udara tidak dapat diabaikan, karena berkat kekuatan ini mereka berhasil tetap bertahan untuk waktu yang lama, menyebabkan alergi musiman.

Gambar 2. Butir serbuk sari cukup kecil untuk ketahanan udara memiliki efek yang signifikan. Sumber: Pikrepo.

Perenang dan pengendara sepeda

-Dalam kasus perenang, mereka menggunakan topi dan mereka mencukur sepenuhnya sehingga resistensi air tidak mengurangi kecepatan.

-Seperti perenang, pengendara sepeda di Counterreloj mengalami resistensi udara, akibatnya helm memiliki desain aerodinamis untuk meningkatkan efisiensi.

Posisi pengendara sepeda juga dalam kelompok dalam kompetisi relevan. Orang yang mengepalai pawai jelas menerima perlawanan udara terbesar, sementara bagi mereka yang menutup pawai, ini hampir nol.

Itu dapat melayani Anda: Kondisi keseimbangan kedua: penjelasan, contoh, latihan

Paracharidists

-Setelah terjun payung membuka parasut, itu terkena gesekan udara kental, menjadi model yang paling tepat yang memiliki kuadrat kecepatan. Dengan cara ini ia mengurangi kecepatannya dan sebagai gosok bertentangan dengan jatuh, ia mencapai nilai batas konstan.

Mobil

-Untuk mobil, koefisien resistensi aerodinamis, konstanta yang ditentukan secara eksperimental dan permukaannya terhadap angin, adalah faktor penentu untuk mengurangi resistensi udara dan mengurangi konsumsi. Itulah sebabnya mereka dirancang dengan kaca depan miring.

Eksperimen Drop Minyak Millikan

-Dalam percobaan drop minyak Millikan, fisikawan Robert Millikan mempelajari pergerakan tetesan minyak di tengah medan listrik yang seragam, menyimpulkan bahwa setiap muatan listrik adalah kelipatan beban elektron.

Untuk ini perlu mengetahui jari -jari tetes, yang tidak dapat ditentukan dengan ukuran langsung, mengingat ukurannya yang kecil. Namun dalam hal ini gesekan kental sangat signifikan dan tetes akhirnya menjadi pengereman. Fakta ini diizinkan untuk menentukan jari -jari tetes dan kemudian muatan listriknya.

Latihan

- Latihan 1

Dalam persamaan untuk gaya gesekan kental dengan kecepatan rendah:

F_menyentuh = ΓV

a) Dimensi apa yang harus dimiliki koefisien gesekan kental?

b) Apa unit γ dalam sistem unit internasional?

Solusi untuk

Tidak seperti koefisien gesekan statis atau kinetik, koefisien gesekan kental memiliki dimensi, yang harus:

Dapat melayani Anda: adhesi fisik: apa itu dan contoh

Kekuatan / kecepatan

Gaya memiliki dimensi massa x panjang /waktu², Sedangkan kecepatan panjang/waktu. Dengan menunjukkannya sebagai berikut:

-Misa: m

-Panjang: l

-Waktu: t

Dimensi koefisien gesekan kental γ adalah:

[M.L /t²] / [L / t] = [m.L.T / l.T²] = M/t

Solusi b

Di SI, unit γ adalah kg/s

- Latihan 2

Dengan mempertimbangkan resistensi yang ditentang air, menemukan ekspresi untuk kecepatan terminal spherite logam yang turun secara vertikal ke tabung yang penuh minyak, dalam kasus: dalam kasus:

A) Kecepatan Rendah

b) kecepatan tinggi

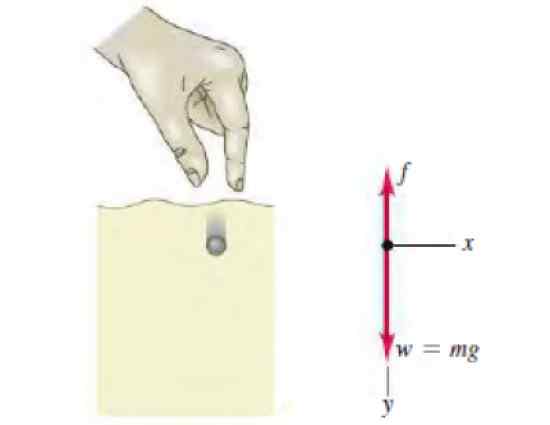Gambar 3. Diagram tubuh bebas dari spherite yang turun ke dalam cairan. Sumber: Sears, Z. Fisika Universitas dengan Fisika Modern.

Solusi untuk

Pada gambar diagram tubuh bebas muncul, menunjukkan dua kekuatan yang bekerja pada spherite: berat turun dan resistansi fluida, sebanding dengan kecepatan, ke atas. Hukum kedua Newton untuk gerakan ini menetapkan yang berikut:

γV_T - mg = 0

Dimana v_T Itu adalah kecepatan terminal, diberikan oleh:

v_T = mg / γ

Solusi b

Jika kita mengira rata -rata pada kecepatan tinggi, model yang sesuai adalah yang dengan kecepatan persegi:

F_menyentuh = ½ ρ.KE.C_D.v²

Jadi:

½ ρ.KE.C_D.v² - mg = 0

D.v² - mg = 0

v = √ [mg / d]

Dalam kedua situasi, semakin besar massa objek, semakin besar kecepatan terminalnya.

Referensi

1. Serway, r., Jewett, J. (2008). Fisika untuk Sains dan Teknik. Volume 1. 7. Ed. Pembelajaran Cengage.
2. Sears, Zemansky. 2016. Fisika Universitas dengan Fisika Modern. 14. Ed. Volume 1.
3. Tipler, hlm. (2006) Fisika untuk Sains dan Teknologi. Edisi ke -5. Volume 1. Editorial dikembalikan.
4. Tippens, hlm. 2011. Fisika: Konsep dan Aplikasi. Edisi ke -7. Bukit McGraw
5. Universitas Sevilla. Kekuatan gesekan. Pulih dari: Laplace.kita.adalah.