Fungsi Karakteristik Konstan, Contoh, Latihan

Itu fungsi konstan Itu adalah nilai di mana nilai dan. Dengan kata lain: fungsi konstan selalu memiliki formulir  f (x) = k, Di mana k Itu adalah bilangan real.

Dengan memberi grafik fungsi konstan dalam sistem koordinat Xy, Itu selalu merupakan garis lurus yang sejajar dengan sumbu horizontal atau sumbu dari X.

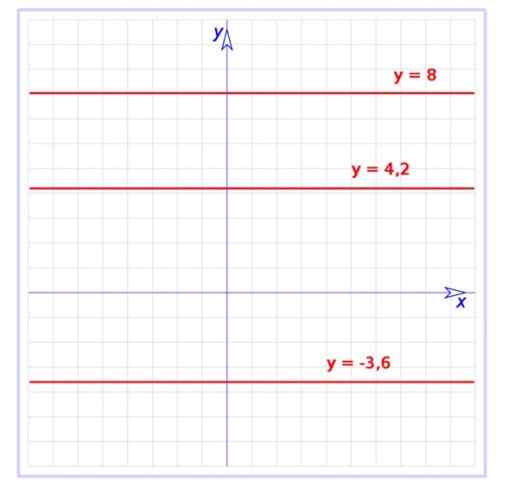
Gambar 1. Grafik beberapa fungsi konstan di bidang Cartesian. Sumber: Wikimedia Commons. Pengguna: Hite [domain publik]

Fungsi ini adalah kasus tertentu dari fungsi terkait, grafiknya juga garis lurus, tetapi dengan lereng. Fungsi konstan memiliki nol tertunda, yaitu, ini adalah garis horizontal, seperti yang terlihat pada Gambar 1.

Ada grafik dari tiga fungsi konstan:

f (x) = -3.6

G (x) = 4.2

H (x) = 8

Semua lurus paralel dengan sumbu horizontal, yang pertama di bawah sumbu itu, sedangkan yang tersisa di atas.

[TOC]

Karakteristik fungsi konstan

Kita dapat meringkas karakteristik utama dari fungsi konstan sebagai berikut:

-Grafiknya adalah garis lurus horizontal.

-Ini memiliki persimpangan yang unik dengan poros Dan, bernilai k.

-Itu terus menerus.

-Penguasaan fungsi konstan (himpunan nilai yang X) adalah himpunan bilangan real R.

-Rute, jangkauan atau kontradiksi (himpunan nilai yang dibutuhkan variabel Dan) hanyalah konstan k.

Contoh

Fungsi diperlukan untuk membangun hubungan antara besaran yang bergantung satu sama lain dalam beberapa cara. Hubungan yang ada di antara mereka dapat dimodelkan secara matematis, untuk mengetahui bagaimana salah satu dari mereka berperilaku ketika yang lain bervariasi.

Dapat melayani Anda: papomudas

Ini membantu membangun model untuk banyak situasi dan membuat prediksi tentang perilaku dan evolusi mereka.

Meskipun kesederhanaannya jelas, fungsi konstan memiliki banyak aplikasi. Misalnya, ketika datang untuk mempelajari magnitudo yang tetap konstan dalam waktu, atau setidaknya, untuk waktu yang cukup.

Dengan cara ini, besarnya berperilaku dalam situasi seperti berikut:

-Itu kecepatan Pelayaran mobil yang bergerak di jalan raya longsor panjang. Selama tidak berhenti atau mempercepat, mobil membawa gerakan bujursangkar yang seragam.

Gambar 2. Jika mobil tidak berhenti atau berakselerasi, ia memiliki gerakan bujursangkar yang seragam. Sumber: Pixabay.

-Kondensor yang sepenuhnya dimuat dan terputus dari sirkuit, memiliki a beban konstan dalam waktu.

-Akhirnya, parkir datar, memelihara a harga Konstan tidak peduli berapa lama sebuah mobil diparkir di sana.

Cara lain untuk mewakili fungsi konstan

Fungsi konstan secara bergantian dapat direpresentasikan sebagai berikut:

f (x) = kx⁰

Karena nilai apapun X Dibesarkan ke 0 memberikan 1 sebagai hasilnya, ekspresi sebelumnya dikurangi menjadi familiar:

f (x) = k

Tentu saja itu terjadi selama nilai k berbeda dari 0.

Itulah sebabnya fungsi konstan juga diklasifikasikan sebagai a fungsi polinomial grade 0, karena eksponen variabel X Itu 0.

Latihan terpecahkan

- Latihan 1

Jawab pertanyaan berikut:

a) Dapatkah ditegaskan bahwa garis yang diberikan oleh x = 4 adalah fungsi konstan? Alasan jawaban Anda.

b) Dapat fungsi konstan memiliki persimpangan dengan sumbu x?

c) adalah fungsi f (x) = w konstanta²?

Menjawab

Berikut adalah grafik garis x = 4:

Dapat melayani Anda: variabel statistik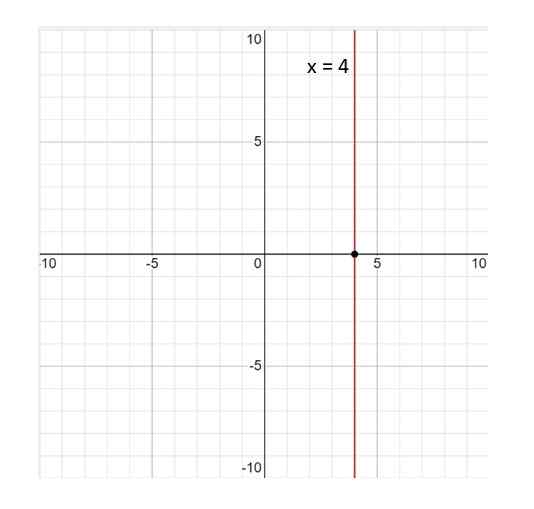 Gambar 3. Grafik garis x = 4. Sumber: f. Zapata.

Baris x = 4 bukan fungsi; Menurut definisi fungsi adalah hubungan sedemikian rupa sehingga dengan setiap nilai variabel X Itu sesuai dengan satu nilai Dan. Dan dalam hal ini ini tidak terpenuhi, karena nilainya x = 4 dikaitkan dengan nilai tak terbatas Dan. Oleh karena itu jawabannya adalah tidak.

Jawaban b

Secara umum, fungsi konstan tidak memiliki persimpangan dengan sumbu X, kecuali itu y = 0, Dalam hal ini adalah sumbu X Dikatakan dengan benar.

Jawaban c

Ya, sejak W Itu konstan, kuadratnya juga. Minat apa itu W Itu tidak tergantung pada variabel input X.

- Latihan 2

Temukan persimpangan antara fungsi f (x) = 5 Dan G (x) = 5x - 2

Larutan

Untuk menemukan persimpangan antara dua fungsi ini, mereka dapat ditulis ulang masing -masing sebagai:

y = 5; y = 5x - 2

Mereka dicocokkan, mendapatkan:

5x - 2 = 5

Yang merupakan persamaan linear tingkat pertama, yang solusinya adalah:

5x = 5+2 = 7

x = 7/5

Titik persimpangan adalah (7/5; 5).

- Latihan 3

Menunjukkan bahwa yang berasal dari fungsi konstan adalah 0.

Larutan

Dari definisi turunan yang Anda miliki:

 f (x) = k

f (x+h) = k

Mengganti definisi:

Di atas masuk akal, karena turunan dari suatu fungsi didefinisikan sebagai kemiringan garis yang bersinggungan ke kurva pada titik tertentu. Fungsi konstan memiliki nol tertunda dan garis singgung apa pun untuk itu juga.

Selain itu, jika kita berpikir tentang turunannya sebagai nilai tukar Dy/dx, Fungsi konstan tidak mengalami perubahan apa pun, oleh karena itu turunannya batal.

Dapat melayani Anda: Prinsip Multiplikasi: Teknik dan Contoh Penghitungan

- Latihan 4

Temukan integral yang tidak terbatas f (x) = k.

Larutan

- Latihan 5

Perusahaan ponsel menawarkan layanan internet tanpa batas dengan tarif tetap membayar $ 15 per bulan. Berapa fungsi harga sesuai waktu?

Larutan

Biarkan P menjadi harga yang harus dibayar dengan waktu $ dan t, yang dapat dinyatakan dalam beberapa hari. Fungsi ini ditetapkan sebagai berikut:

P (t) = 15

- Latihan 6

Grafik versus waktu berikut sesuai dengan pergerakan partikel.

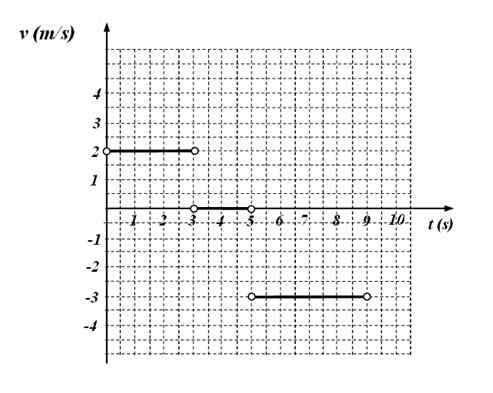Gambar 4. Fungsi V (T) Grafik Fungsi untuk Latihan 6. Sumber: f. Zapata.

Itu diminta:

a) Tulis ekspresi untuk fungsi kecepatan sebagai fungsi waktu V (t).

b) Temukan jarak yang ditempuh oleh ponsel dalam interval waktu antara 0 dan 9 detik.

Solusi untuk

Grafik yang menunjukkan itu:

-V = 2 m/s Dalam interval waktu antara 0 dan 3 detik

-Ponsel ditahan antara 3 dan 5 detik, karena dalam interval ini kecepatan bernilai 0.

-V = - 3 m/s Antara 5 dan 9 detik.

Ini adalah contoh dari sepotong potongan, atau fungsi di bagian, yang pada gilirannya terdiri dari fungsi konstan, hanya berlaku untuk interval waktu yang ditunjukkan. Disimpulkan bahwa fungsi yang dicari adalah:

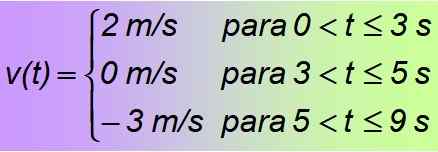
Solusi b

Dari grafik V (t) Jarak yang ditempuh oleh ponsel dapat dihitung, yang secara numerik sama dengan area rendah/pada kurva. Cara ini:

-Jarak ditempuh antara 0 dan 3 detik = 2 m/s . 3 s = 6 m

-Antara 3 dan 5 detik ia ditahan, oleh karena itu ia tidak menempuh jarak apa pun.

-Jarak menempuh antara 5 dan 9 detik = 3 m/s . 4 s = 12 m

Total ponsel tur 18 m. Lihat bahwa meskipun kecepatannya negatif dalam interval antara 5 dan 9 detik, jarak yang ditempuh positif. Apa yang terjadi adalah bahwa selama interval waktu itu, ponsel telah mengubah arti kecepatannya.

Referensi

1. Geogebra. Fungsi konstan. Pulih dari: geogebra.org.
2. Maplesoft. Fungsi konstan. Dipulihkan dari: Maplesoft.com.
3. Wikilibros. Perhitungan dalam variabel/fungsi/fungsi konstan. Pulih dari: is.Wikibooks.org.
4. Wikipedia. Fungsi konstan. Diperoleh dari: di.Wikipedia.org
5. Wikipedia. Fungsi konstan. Pulih dari: is.Wikipedia.org.