Properti Fungsi Eksponensial, Contoh, Latihan

Itu Fungsi eksponensial Ini adalah fungsi matematika yang sangat penting untuk banyak aplikasi yang dimilikinya. Itu didefinisikan sebagai berikut:

f (x) = b^X, Dengan b> 0 dan b ≠ 1

Di mana b adalah konstanta nyata selalu positif dan berbeda dari 1, yang dikenal sebagai basis. Perhatikan bahwa variabel nyata X ditemukan di eksponen, Dengan cara ini f (x) selalu menjadi bilangan real.

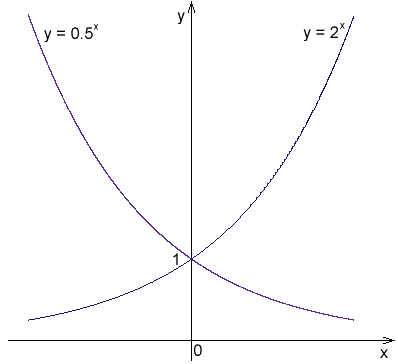Gambar 1. Fungsi eksponensial dengan basis 2 dan 1/2

Contoh fungsi eksponensial adalah sebagai berikut:

-f (x) = 2^X

-g (x) = 5⋅e^-3x

-H (x) = 4⋅ (10^2x)

Ini adalah fungsi yang tumbuh - atau menurun, sesuai dengan tanda eksponen - sangat cepat, jadi ada pembicaraan tentang "pertumbuhan eksponensial" ketika beberapa besarnya meningkat dengan sangat cepat. Inilah sebabnya mengapa mereka tepat untuk memodelkan pertumbuhan makhluk hidup, seperti bakteri.

Aplikasi lain yang sangat menarik adalah menarik minat majemuk. Semakin banyak uang yang Anda miliki dalam suatu akun, semakin banyak minat, dan mereka dapat menghitung setiap interval waktu tertentu, sekecil yang Anda inginkan.

Dengan bantuan fungsi logaritmik, yang merupakan fungsi terbalik dari eksponensial, dapat diketahui setelah berapa lama modal tertentu meningkat ke nilai tertentu.

[TOC]

Properti Fungsi Eksponensial

Gambar 2. Contoh fungsi eksponensial. Sumber: f. Zapata.

Berikut ini adalah sifat umum dari setiap fungsi eksponensial:

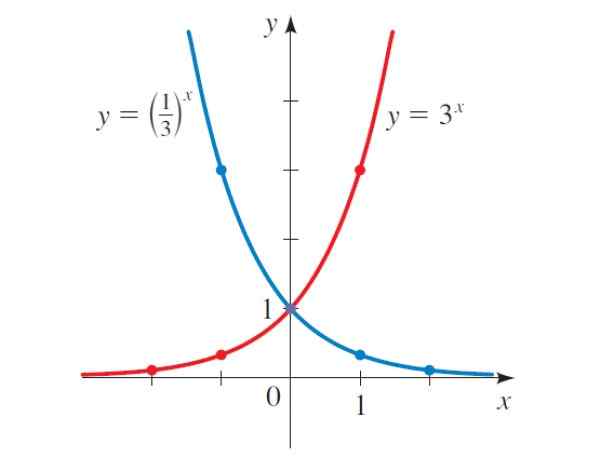
-Grafik dari setiap fungsi eksponensial selalu memotong sumbu vertikal pada titik (0,1), seperti yang dapat dilihat pada Gambar 2. Ini karena b⁰ = 1 untuk nilai b apa pun.

-Fungsi eksponensial tidak berpotongan pada sumbu x, pada kenyataannya sumbu ini adalah asimptot horizontal untuk fungsi tersebut.

-Sejak b¹ = b, titik (1, b) selalu menjadi milik grafik fungsi.

Itu bisa melayani Anda: prisma hepagonal

-Domain fungsi eksponensial adalah himpunan bilangan real dan f (x) = b^X Itu terus menerus dalam semua domainnya.

-Kisaran fungsi eksponensial adalah semua bilangan real lebih besar dari 0, yang juga diperhatikan dengan grafik.

-Fungsi eksponensial adalah satu per satu, yaitu, masing -masing nilai x milik domain fungsi, memiliki gambar yang unik dalam set kedatangan.

-Kebalikan dari eksponensial adalah fungsi logaritmik.

Sifat tertentu dari fungsi eksponensial

Seperti yang telah kami katakan sebelumnya, fungsi eksponensial dapat meningkat atau menurun.

Jika grafik Gambar 2 dipelajari dengan cermat, dicatat bahwa jika b> 1, fungsinya tumbuh, misalnya y = 3^X, Tetapi dalam kasus y = (1/3)^X, dengan b < 1, la función decrece.

Kami memiliki dua jenis fungsi eksponensial dengan sifat -sifat tertentu berikut:

Untuk b> 1

-Fungsinya selalu berkembang.

-Ketika nilai B meningkat, fungsi tumbuh lebih cepat, misalnya y = 10^X tumbuh lebih cepat dari y = 2^X.

-Ketika variabel lebih besar dari 0, fungsi memperoleh nilai lebih besar dari 1, yaitu:

Untuk x> 0: y> 1

-Dan jika x<0, entonces f(x) < 1.

Untuk b < 1

-Fungsinya selalu berkurang.

-Dengan mengurangi nilai B, fungsi berkurang lebih cepat. Misalnya y = (1/5)^X berkurang lebih cepat dari y = (1/3)^X.

-Untuk nilai x lebih rendah dari 0, fungsi mengambil nilai lebih besar dari 1, yaitu:

Untuk x 1

-Akhirnya, saat x> 0, lalu dan < 1.

Contoh fungsi eksponensial

Fungsi eksponensial sangat berguna untuk pemodelan fenomena dalam sains dan ekonomi, seperti yang akan kita lihat di bawah:

Fungsi eksponensial alami

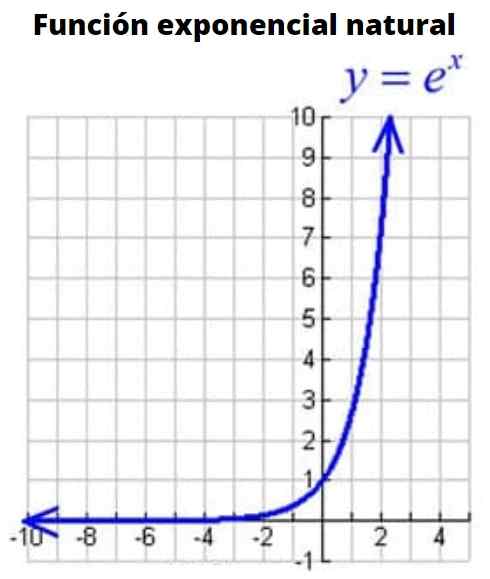Gambar 3: Grafik fungsi eksponensial alami

Ini adalah fungsi yang basisnya adalah angka e atau euler, angka irasional yang nilainya:

Dapat melayani Anda: sudut tambahan: apa itu, perhitungan, contoh, latihan

E = 2.718181828…

Basis ini, bahkan jika itu bukan bilangan bulat, bekerja dengan sangat baik untuk berbagai aplikasi. Oleh karena itu dianggap sebagai dasar paling penting dari semua fungsi eksponensial. Fungsi eksponensial alami diekspresikan dengan cara matematika sebagai:

f (x) = e^X

Fungsi eksponensial sering muncul dalam probabilitas dan statistik, karena berbagai distribusi probabilitas, seperti distribusi normal, Poisson dan lainnya, dapat diekspresikan melalui fungsi eksponensial.

Bunga majemuk terus menerus

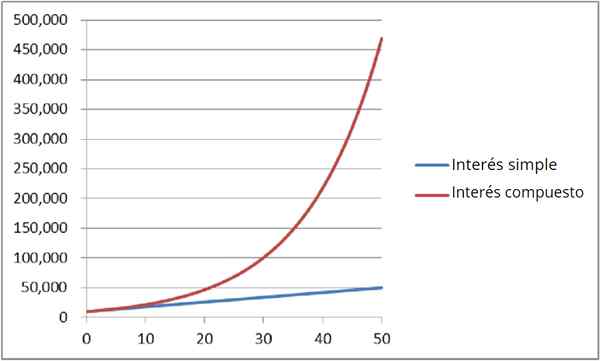Gambar 4: Perbandingan bunga sederhana dan majemuk

Itu juga disebut Kapitalisasi Berkelanjutan. Untuk mengetahui jumlah uang KE Anda punya setelahnya T Bertahun -tahun, ekspresi eksponensial digunakan:

A (t) = p ⋅ e^Rt

Di mana P adalah jumlah uang yang awalnya disimpan, R adalah tingkat bunga per tahun dan akhirnya T adalah jumlah tahun.

Pertumbuhan bakteri

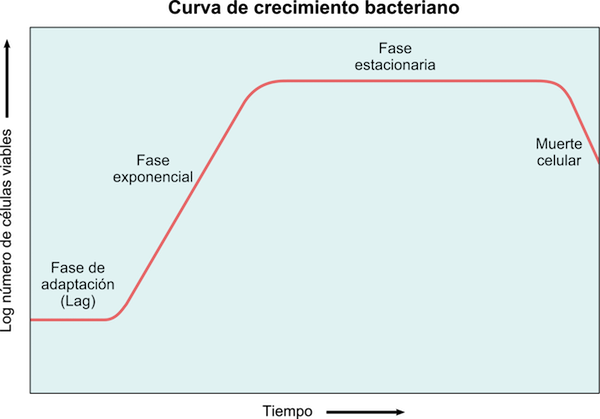Gambar 5: Kurva pertumbuhan bakteri di mana fase latensi, eksponensial, stasioner dan kematian diamati

Bakteri tumbuh secara eksponensial, sehingga pertumbuhan dapat dimodelkan oleh:

N (t) = n_{salah satu} ⋅ e ^KT

Di mana n (t) adalah populasi yang ada setelah waktu t (hampir selalu dalam jam), n_{salah satu} Ini adalah populasi awal dan k adalah konstanta yang tergantung pada jenis bakteri dan kondisi di mana nutrisi tersedia.

Pembusukan Radioaktif

Nukleus tertentu di alam tidak stabil, sehingga mereka menolak untuk berubah menjadi yang lebih stabil, suatu proses yang bisa sangat singkat atau memakan waktu ribuan tahun, tergantung pada isotopnya. Selama peluruhan radioaktif, partikel -partikel yang dipancarkan dan kadang -kadang juga foton.

Beberapa isotop radioaktif memiliki aplikasi medis, misalnya yodium radioaktif I-131, yang digunakan dokter dalam diagnosis dan pengobatan kondisi tiroid tertentu.

Peluruhan radioaktif dimodelkan oleh fungsi eksponensial.

Dapat melayani Anda: berapa persepuluh yang ada di satu unit?

Latihan terpecahkan

Persamaan di mana yang tidak diketahui muncul sebagai eksponen disebut persamaan eksponensial. Untuk menghapus nilai yang tidak diketahui, manipulasi aljabar yang berbeda digunakan dan penggunaan fungsi logaritma, yang merupakan fungsi sebaliknya dari eksponensial.

Mari kita lihat beberapa latihan terpecahkan yang menggambarkan intinya.

- Latihan 1

Selesaikan persamaan eksponensial berikut:

hingga 5^X = 625

b) 5^X = 2^X-1

Solusi untuk

Angka 625 adalah kelipatan 5, pada dasarnya, ketika membusuknya kami menemukan itu:

625 = 5⁴

Oleh karena itu kita bisa menulis:

5^X = 5⁴

Karena pangkalannya sama dengan kedua kiri dan kanan, kita dapat mencocokkan eksponen dan mendapatkan:

x = 4

Solusi b

Untuk latihan ini kita tidak dapat menggunakan teknik yang sebelumnya digunakan, karena pangkalannya tidak sama. Tapi kita bisa menerapkan logaritma di kedua sisi kesetaraan, dengan cara ini:

5^X = 2^X-1

Log (5^X) = log (2^X-1)

Sekarang properti logaritma berikut diterapkan:

Log m^N = n⋅log m

Dan tetap:

x⋅log 5 = (x-1) ⋅log 2

x⋅ (log 5 - log 2) = -log 2

x = - log 2 ÷ (log 5 - log 2)

- Latihan 2

Tunjukkan fungsi apa masing -masing grafik yang ditunjukkan di bawah ini sesuai:

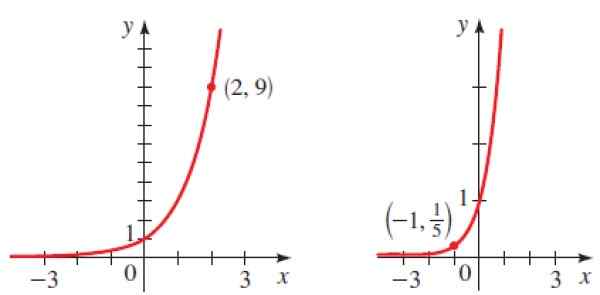Gambar 6. Grafik Parast Fungsi eksponensial dari latihan yang diselesaikan 2. Sumber: Stewart. J. Prekalkulasi.

Solusi untuk

Karena ini adalah grafik yang tumbuh, B lebih besar dari 1 dan kita tahu bahwa titik (2.9) milik grafik, oleh karena itu: oleh karena itu:

y = b^X → 9 = b²

Kami tahu itu 3² = 9, oleh karena itu b = 3 dan fungsinya adalah y = 3^X

Solusi b

Sekali lagi kami mengganti titik yang diberikan (-1, 1/5) di y = b^X mendapatkan:

1/5 = b^-1 = 1/b

Kemudian B = 5 dan fungsi yang dicari adalah:

y = 5^X

Referensi

1. Figuera, J. 2000. Matematika 1. Diversifikasi. Edisi Co-Bo.
2. Gid Hoffmann, J. Pemilihan Masalah Matematika untuk ke -4. Tahun. Ed. Spphinx.
3. Jiménez, r. 2008. Aljabar. Prentice Hall.
4. Larson, r. 2010. Perhitungan variabel. 9NA. Edisi. Bukit McGraw.
5. Stewart, J. 2006. PRECCCULMENT: Matematika untuk Perhitungan. Ke -5. Edisi. Pembelajaran Cengage.