Fungsi homografi cara grafik, latihan terpecahkan

Itu fungsiHomografi atau rasional Ón Ini adalah jenis fungsi matematika yang terdiri dari pembagian dua komponen polinomial. Ini mematuhi bentuk p (x)/q (x), di mana q (x) tidak dapat mengambil bentuk nol.

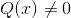
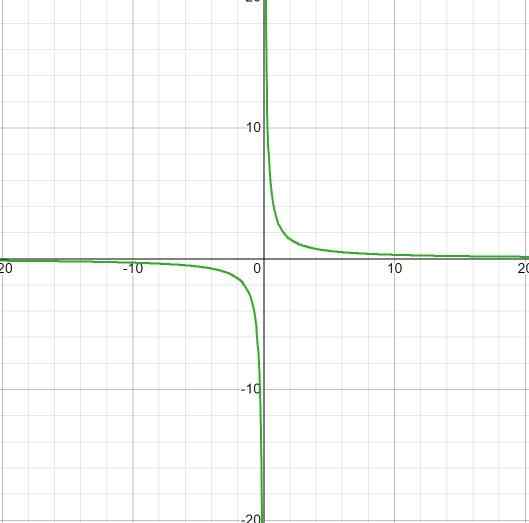
Misalnya ekspresi (2x - 1)/(x + 3) sesuai dengan fungsi homografi dengan p (x) = 2x - 1 y q (x) = x + 3.

Sumber: Pixabay.com

Fungsi homografi merupakan bagian studi fungsi analitik, diperlakukan dari pendekatan grafik dan dari studi domain dan rentang. Ini karena pembatasan dan fondasi yang harus diterapkan untuk resolusi mereka.

[TOC]

Apa itu fungsi homografik?

Mereka adalah ekspresi rasional dari variabel unik, meskipun ini tidak berarti bahwa tidak ada ekspresi yang sama untuk dua atau lebih variabel, di mana ia sudah berada di hadapan tubuh di ruang yang mematuhi pola yang sama dengan fungsi homografi di level.

Mereka memiliki akar nyata dalam beberapa kasus, tetapi adanya asimtot vertikal dan horizontal selalu dipertahankan, serta juga interval pertumbuhan dan penurunan. Umumnya hanya satu dari tren ini yang ada, tetapi ada ekspresi yang mampu menunjukkan keduanya dalam pengembangannya.

Domainnya dibatasi oleh akar penyebut, karena tidak ada pembagian antara nol bilangan real.

Fungsi homografi campuran

Mereka sangat sering dalam perhitungan, terutama diferensial dan komprehensif, diperlukan untuk mendapatkan dan anti -anel di bawah formula tertentu. Beberapa yang paling umum diklasifikasikan di bawah ini.

Pasangan fungsi homografi ke -n

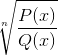
Tidak termasuk semua elemen domain yang membuat argumen negatif. Akar yang ada di setiap polinomial menunjukkan nilai nol saat dievaluasi.

Nilai -nilai ini diterima oleh radikal, meskipun pembatasan mendasar dari fungsi homografi harus dipertimbangkan. Di mana q (x) tidak dapat menerima nilai nol.

Dapat melayani Anda: Fungsi Transenden: Jenis, Definisi, Properti, Contoh

Solusi interval harus dicegat:

Untuk mencapai persimpangan, metode tanda dapat digunakan, antara lain.

Fungsi Homografi Logaritma

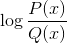
Tidak termasuk nilai domain yang melempar interval negatif dan nol. Karena nol sudah dikecualikan dari penyebut, solusi dari: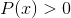

Juga umum untuk menemukan kedua ekspresi dalam satu, di antara kombinasi lain yang mungkin.

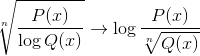
Cara grafik fungsi homografi?

Fungsi homografi sesuai secara grafis dengan hiperbola di pesawat. Yang diangkut secara horizontal dan vertikal sesuai dengan nilai -nilai yang menentukan polinomial.

Ada beberapa elemen yang harus kita definisikan untuk grafik fungsi rasional atau homografi.

Perkebunan

Yang pertama adalah akar atau nol dari fungsi p dan q.

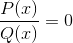
Nilai -nilai yang dicapai akan dilambangkan pada sumbu x dari grafik. Menunjukkan persimpangan grafik dengan sumbu.

Asimptot vertikal

Sesuai dengan garis vertikal, yang membatasi grafik sesuai dengan tren yang mereka sajikan. Mereka menyentuh sumbu x dalam nilai -nilai yang membuat penyebut nol dan tidak akan pernah disentuh oleh grafik fungsi homografi.

Asimptot horizontal

Diwakili oleh garis jahitan horizontal, membatasi batas yang tidak akan didefinisikan pada titik yang tepat. Tren akan diamati sebelum dan sesudah baris ini.

Untuk menghitungnya, kita harus menggunakan metode yang mirip dengan metode l'Hopital, digunakan untuk menyelesaikan batas fungsi rasional yang cenderung tak terbatas. Koefisien kekuatan tertinggi dalam pembilang dan penyebut fungsi harus diambil.

Misalnya, ekspresi berikut memiliki asimptot horizontal pada y = 2/1 = 2.

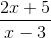
Interval pertumbuhan

Nilai -nilai yang dipesan akan memiliki tren yang ditandai dalam grafik karena asimtot. Dalam kasus pertumbuhan, fungsi akan meningkat dari nilai karena elemen domain dari kiri ke kanan dievaluasi.

Dapat melayani Anda: 60 pembagi

Penurunan interval

Nilai yang dipesan akan berkurang karena elemen domain dari kiri ke kanan dievaluasi.

Lompatan yang ditemukan dalam nilai tidak akan diperhitungkan sebagai peningkatan atau berkurang. Ini terjadi ketika grafik dekat dengan vertikal atau horizont.

Persimpangan dengan y

Membuat nol nilai x, adalah persimpangan dengan sumbu ordinat. Ini adalah fakta yang sangat berguna untuk mendapatkan grafik fungsi rasional.

Contoh

Tentukan grafik dari ekspresi berikut, temukan akar, asimtot vertikal dan horizontal, pertumbuhan dan penurunan interval dan persimpangan dengan sumbu dari yang dipesan.

Latihan 1

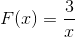
Ekspresi tidak memiliki akar, karena memiliki nilai konstan dalam pembilang. Pembatasan untuk diterapkan akan x berbeda dari nol. Dengan asimptot horizontal pada y = 0, dan vertikal asimptot pada x = 0. Tidak ada titik persimpangan dengan sumbu dan.

Diamati bahwa tidak ada interval pertumbuhan bahkan dengan lompatan dari lebih sedikit ke lebih tidak terbatas pada x = 0.

Interval penurunan adalah

ID: (-∞; o) u (0, ∞)

Latihan 1.2

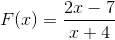
2 Polinomial diamati seperti dalam definisi awal, jadi kami melanjutkan sesuai dengan langkah -langkah yang ditetapkan.

Akar yang ditemukan adalah x = 7/2 yang dihasilkan dari menyamakan fungsi.

Asimptot vertikal adalah pada x = - 4, yang merupakan nilai yang dikecualikan dari domain karena kondisi fungsi rasional.

Asimptot horizontal adalah dalam y = 2, ini setelah membagi 2/1, koefisien variabel grade 1.

Ini memiliki persimpangan dengan yang dipesan di y = - 7/4. Nilai ditemukan setelah menyamakan x ke nol.

Itu dapat melayani Anda: fraksi setara dengan 3/5 (solusi dan penjelasan)

Fungsi tumbuh secara konstan, dengan lompatan dari lebih dari yang lebih rendah di sekitar root x = -4.

Interval pertumbuhannya adalah (-∞, - 4) u ( - 4, ∞).

Ketika nilai x hampir tak terbatas, fungsi mengambil nilai mendekati 2. Hal yang sama terjadi ketika X mendekati lebih tak terbatas.

Ekspresi mendekati lebih tak terbatas saat dievaluasi di - 4 di sebelah kiri, dan kurang tak terbatas saat dievaluasi di - 4 di sebelah kanan.

Latihan 2

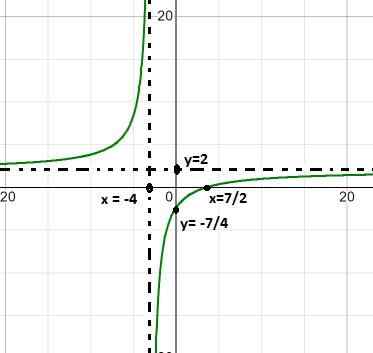
Grafik fungsi homografi berikut diamati:

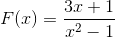
Jelaskan perilaku, akar, asimtot vertikal dan horizontal, pertumbuhan dan penurunan interval dan persimpangan dengan sumbu yang dipesan.

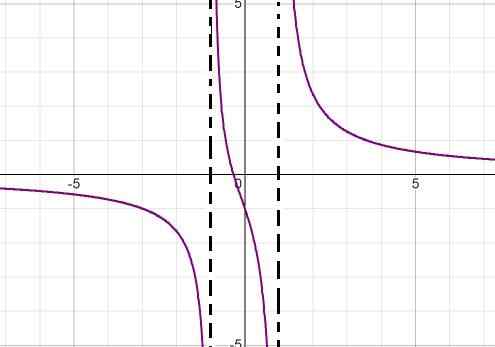
Denominator ekspresi menunjukkan dengan memperhitungkan perbedaan kotak (x + 1) (x - 1) nilai -nilai akar. Dengan cara ini kedua asimtot vertikal dapat didefinisikan sebagai:

x = -1 dan x = 1

Asimptot horizontal sesuai dengan sumbu absis karena kekuatan utama ada di denominator.

Root -nya ditentukan oleh x = -1/3.

Ekspresi selalu berkurang dari kiri ke kanan. Itu mendekati nol saat cenderung tak terbatas. Kurang tak terbatas saat mendekati -1 di sebelah kiri. Lebih tak terbatas saat mendekati -1 di sebelah kanan. Kurang tak terbatas saat mendekati 1 di sebelah kiri dan lebih tak terbatas saat mendekati 1 di sebelah kanan.

Referensi

1. Perkiraan dengan fungsi rasional. Donald J. Orang baru. Soc Mathematical Amerika., 31 Desember. 1979
2. Fungsi Peringkat Orthogonal. University of La Laguna Tenerife Adhemar Bultheel, Adhemar Bultheel, Pablo Gonzalez-Vera, Erik Hendriksen, Olav Njstad. Cambridge University Press, 13 Feb. 1999
3. Perkiraan peringkat fungsi nyata. P. P. Petrushev, Vasil Atanasov Popov. Cambridge University Press, 3 Maret. 2011
4. Fungsi Aljabar. Gilbert Ames Bliss. Couer Corporation, 1 Jan. 2004
5. Majalah Masyarakat Matematika Spanyol, 5-6 volume. Masyarakat Matematika Spanyol, Madrid 1916