Fungsi variabel nyata nyata dan representasi grafisnya

A fungsi variabel nyata nyata Ambil nomor milik set bilangan real dan mengaitkannya dengan nilai lain, juga nyata, melalui aturan korespondensi yang unik. Ini berarti bahwa bilangan real memperoleh, melalui aturan ini, gambar yang unik.

Variabel keberangkatan numerik biasanya ditunjuk oleh huruf x, sedangkan gambarnya adalah huruf dan. Di sisi lain, dengan aturan korespondensi yang menghubungkannya juga dipanggil dengan beberapa huruf alfabet lainnya, seperti fungsi "f", meskipun yang lain dapat digunakan.  Dalam notasi kompak itu ditulis:

f: x → y = f (x)

Gambar 1. Grafik fungsi polinomial nyata

Ke variabel  X itu disebut variabel bebas, selagi Dan Ini adalah variabel tak bebas. Fungsi dapat diekspresikan dalam beberapa cara, misalnya melalui pernyataan matematika seperti ini:

• f (x) = 2x −3
• H (x) = −3x²
• 

Bentuk ekspresi lain adalah melalui grafik, yang sangat berguna karena memungkinkan Anda untuk menghargai perilaku fungsi sekilas. Membangun grafik sangat sederhana menggunakan sistem koordinat cartesian, di mana rekan [x, f (x)] direpresentasikan sebagai titik di pesawat. Kemudian mereka bergabung dengan garis yang lembut dan kontinu, Anda dapat melihat bagaimana fungsinya.

Contoh

Untuk membangun grafik, Anda dapat menggunakan tabel nilai di mana titik -titik ke grafik ditempatkan. Untuk nilai x variabel dipilih milik domain fungsi, yaitu, yang ketika diganti dalam rumus, pada gilirannya menunjukkan bilangan real.

Setelah nilai -nilai x telah dipilih, gambarnya y = f (x) ditentukan, dan dengan cara ini berpasangan titik [x, f (x)] yang akan diperoleh grafik.

Dapat melayani Anda: fungsi homografi: cara grafik, latihan terpecahkan

Ada beberapa titik yang penting dan harus dimasukkan dalam tabel: yang ada di mana grafik memotong ke sumbu koordinat, bahwa jika ada, karena tidak semua fungsi memotongnya.

Untuk menghitungnya, lanjutkan sebagai berikut:

-Persimpangan dengan sumbu dan: x = 0 dibuat dalam rumus fungsi dan nilai yang sesuai dihitung.

-Persimpangan dengan sumbu x: Y = 0 selesai dan persamaan f (x) = 0 diselesaikan.

Selanjutnya, sistem koordinat cartesian ditarik dan masing -masing titik diplot, yang kemudian bergabung dengan garis yang lembut dan kontinu jika memungkinkan.

Contoh 1

Bangun tabel nilai dan grafik dari fungsi berikut:

f (x) = x² −4

Sebelum memulai, Anda harus menemukan domain fungsi, yang merupakan himpunan nilai nyata yang ada fungsi. Karena ini adalah fungsi kuadratik, nilai x apa pun yang dimiliki bilangan real memiliki gambar nyata, menurut f (x).

Kemudian, tabel dapat dibangun dengan memilih nilai x apa pun, dan yang paling sederhana adalah memulai dengan persimpangan grafik dengan sumbu, jika ada. Setelah menemukannya, maka poin -poin lain dicari untuk melengkapi tabel.

Untuk x = 0

f (0) = -4

Oleh karena itu, titik pertama dalam tabel adalah (0, -4). Ini adalah persimpangan grafik dengan sumbu dan.

Untuk y = 0

Maka y = 0 dilakukan dan persamaan hasilnya diselesaikan:

X² −4 = 0

X² = 4

Solusi dari persamaan ini adalah: x₁= 2 dan x₂= -2. Oleh karena itu ada dua persimpangan dengan sumbu x, yang merupakan titik: (−2.0) dan (2.0).

Dapat melayani Anda: angka sempurna: cara mengidentifikasi mereka dan contoh

Sekarang Anda dapat menemukan lebih banyak poin untuk ditambahkan ke tabel nilai:

Untuk x = 1

f (1) = (1)² - 4 = −3

Untuk x = - 1

f (−1) = (−1)² - 4 = −3

Untuk x =  3

f (3) = (3)² - 4 = 5

Untuk x =  -3

f (−3) = (−3)² - 4 = 5

Tabel nilai

Tabel berikut menunjukkan titik yang diperoleh, yang akan berfungsi untuk membangun grafik f (x):

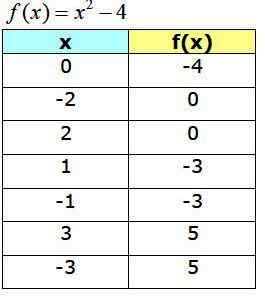Grafik fungsi f (x) = x² −4

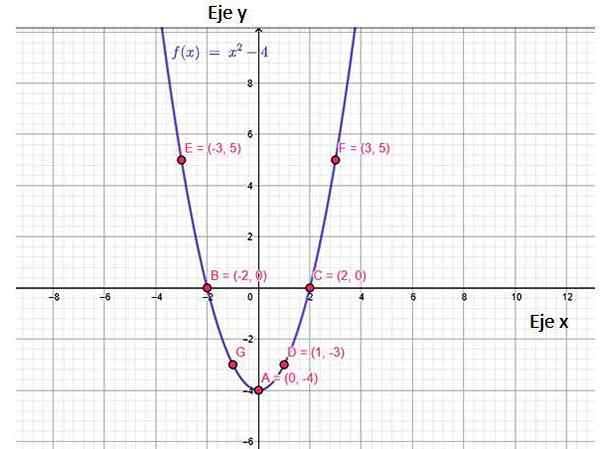Gambar 2. Fungsi grafik fungsi f (x), menunjukkan beberapa titik yang dimiliki olehnya, termasuk persimpangan dengan sumbu. Sumber: f. Zapata, melalui geogebra.

Grafik fungsi ini adalah perumpamaan, yang terbuka dan memiliki pada titik minimum, yang disebut puncak, koordinat (0, −4). Sangat menarik untuk dicatat bahwa nilai f (x) dimulai pada y = -4 hingga ∞. Ini jangkauan dari fungsi tersebut.

Dari grafik dapat disimpulkan bahwa fungsinya kontinu, menurun dalam interval (−∞, 0) dan meningkat dari sana.

Contoh 2

Memiliki grafik fungsi, dimungkinkan untuk mengetahui domainnya, jangkauannya, persimpangan yang dimilikinya dengan sumbu dan memvisualisasikan perilaku umumnya (pertumbuhan dan penurunan).

Di bawah ini adalah grafik fungsi polinomial:

f (x) = - x⁴+4x²+1

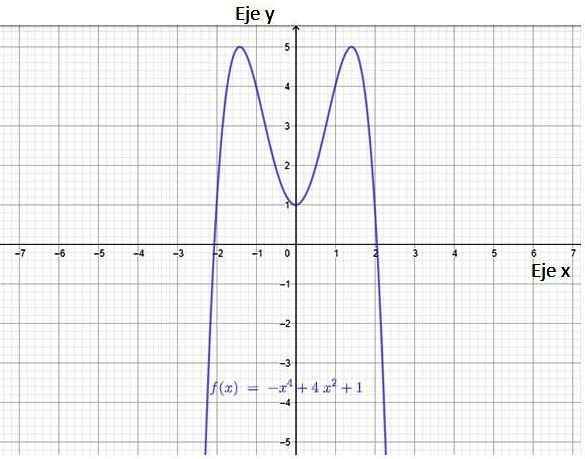Gambar 3. Grafik fungsi polinomial. Sumber: f. Zapata melalui Geogebra.

Dari gambar itu mengikuti bahwa fungsi memiliki dua persimpangan dengan sumbu x, titik (-2.0) dan (2.0). Ini juga memiliki persimpangan dengan sumbu y, titik (0,1).

Domain fungsi polinomial adalah set lengkap bilangan real, juga diperingatkan bahwa fungsinya kontinu dan memiliki simetri di sekitar sumbu vertikal. Memang, dapat diverifikasi bahwa fungsi ini Simetri untuk. Suatu fungsi adalah bahkan jika bertemu:

Dapat melayani Anda: Teorema Hijau, Demonstrasi, Aplikasi dan Latihan

f (x) = f (-x)

Pembaca dapat memverifikasi bahwa dengan mengganti -x dalam fungsi, tidak diubah.

Ada dua titik menarik, yaitu pada ketinggian y = 5, adalah nilai maksimum fungsi. Kisaran fungsi ini, yaitu, himpunan nilai yang diambil variabel dan, meluas dari -∞ ke y = 5 secara tepat.

Untuk mengetahui nilai -nilai x yang gambarnya y = 5, nilai ini diganti dalam fungsi:

5 = - x⁴+4x²+1

Dan persamaan ini diperoleh:

- X⁴ + 4x² - 4 = 0

Yang solusinya −√2 dan + √2. Nah, fungsinya adalah:

-Pertumbuhan Dari x -∞ ke x = −√2

-Menurun Dari x = −√2 ke x = 0

-Pertumbuhan Dari x = 0 hingga x = + √2

-Menurun Dari x = + √2 dan seterusnya.

Olahraga diselesaikan

Bangun grafik fungsi berikut:

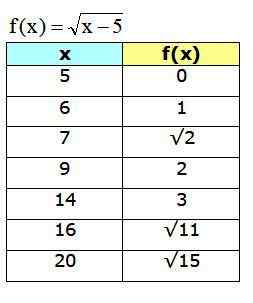
f (x) = √ (x-5)

Larutan

Pertama, Anda harus menentukan domain fungsi, untuk mengetahui nilai x mana yang dapat dipilih untuk membangun tabel. Dalam kasus fungsi yang diusulkan, jumlah dalam root harus selalu positif atau sama dengan 0, oleh karena itu: oleh karena itu:

x - 5 ≥ 0

x ≥ 5

Oleh karena itu, hanya nilai yang lebih besar dari atau sama dengan 5 yang dapat dipilih untuk tabel. Adapun persimpangan dengan sumbu koordinat, satu -satunya kemungkinan adalah melakukan y = 0, dan kemudian x = 5.

Tidak ada gunanya melakukan x = 0 untuk fungsi ini, karena nilai ini bukan milik domain.

Grafik yang diperoleh adalah:

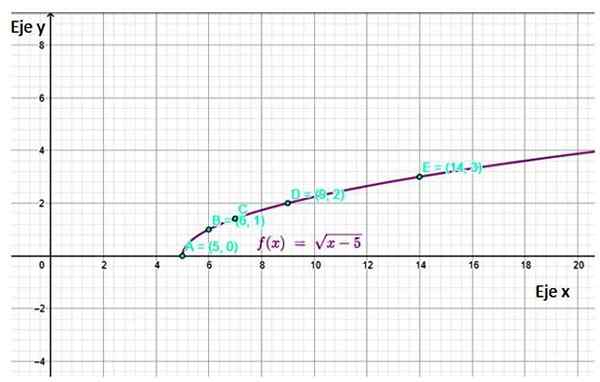Gambar 4. Grafik fungsi f (x) yang menunjukkan beberapa titik yang dihitung dalam tabel. Sumber: f. Zapata melalui Geogebra.

Referensi

1. Zona e-math. Jenis fungsi. Pulih dari: emathzone.com.
2. Hoffman, J.G. Pemilihan masalah matematika. Ed. Spphinx.
3. Matematika itu menyenangkan. Referensi Fungsi Commons. Pulih dari: Mathisfun.com.
4. Requena, b. Rumus alam semesta. Jenis fungsi. Pulih dari: universoformulas.com.
5. Stewart, J. 2006. PRECCCULMENT: Matematika untuk Perhitungan. Ke -5. Edisi. Pembelajaran Cengage.