Fungsi Trigonometri Dasar, di bidang Cartesian, Contoh, Latihan

Itu fungsi trigonometri Dari variabel nyata mereka sesuai dengan sudut apa pun (diekspresikan dalam radianes), alasan trigonometri, yang dapat berupa sinus, cosinus, garis singgung, cotangent, secant dan pemanen.

Dengan cara ini kita memiliki enam fungsi trigonometri: sinus, cosinus, garis singgung, pemanen, pengeringan dan cotangent.

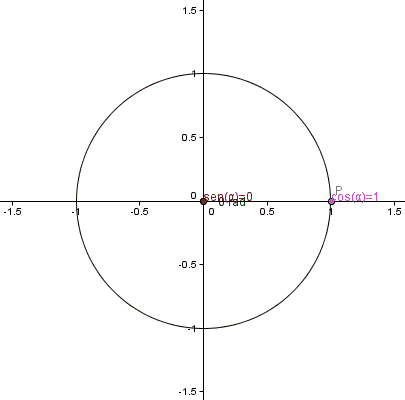Gambar 1. Animasi Lingkaran Trigonometri. Sumber: Wikimedia Commons.

Fungsi trigonometri untuk sudut antara 0 dan 2π didefinisikan dengan bantuan lingkar kesatuan, dari Radio 1 dan yang pusatnya bertepatan dengan asal usul sistem koordinat Cartesian: titik (0,0).

Kita dapat menemukan titik p dari koordinat (x, y) pada keliling ini.

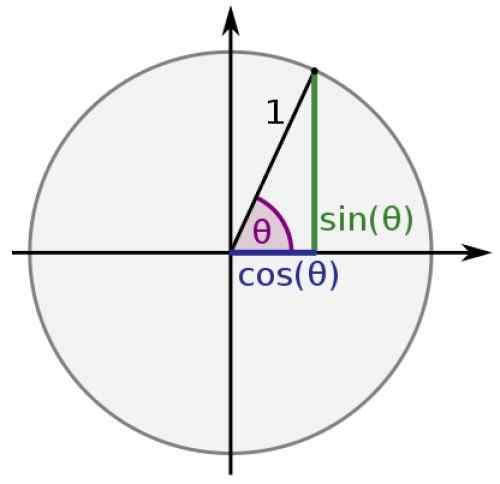
Segmen yang menyatukan asal dengan P, bersama -sama dengan segmen masing -masing yang menyatukan proyeksi P pada sumbu koordinat, membentuk segitiga persegi panjang, yang alasan trigonometriknya dikenal sebagai kutipan antara sisi segitiga. Jadi:

• sin θ = lawan /hypotenusa cateto
• cos θ = Cateto yang berdekatan /hipotenusa
• TG θ = Cateto yang berlawanan /cateto yang berdekatan

Dan sekarang alasan yang merupakan kebalikan dari hal di atas:

• Sec θ = Hypotenuse /Cateto yang berdekatan
• Bahaya θ = hypotenusa /cateto berlawanan
• CTG θ = cateto yang berdekatan /lawan cateto

Di lingkaran kesatuan, hipotenus dari segitiga mana pun sama dengan 1 dan kategorinya bernilai x dan y, lalu:

sin θ = y

cos θ = x

Gambar 2. Segitiga kanan di lingkaran unit. Sumber: Wikimedia Commons.

Dengan cara ini, fungsi sinus dan kosinus selalu memperoleh nilai antara -1 dan 1, sedangkan yang tersisa:

tg θ = y/x

bahaya θ = 1/y

Dtk θ = 1/x

Mereka tidak didefinisikan saat X salah satu Dan Mereka bernilai 0.

[TOC]

Fungsi trigonometri di bidang Cartesian

Seperti yang akan kita lihat di bawah, fungsi trigonometri ditandai dengan menjadi berkala. Oleh karena itu mereka tidak bersifat bypective, kecuali dalam domain terbatas.

Fungsi f (x) = sin x

Mulai dari lingkaran trigonometri pada titik p (1.0), sudutnya adalah 0 radian. Kemudian jari -jari berputar dalam pengertian anti -adorer dan fungsi sen x tumbuh secara bertahap sampai mencapai radian π/2 (90º), setara dengan 1.Sekitar 571 radian.

Dapat melayani Anda: sudut tambahan: apa itu, perhitungan, contoh, latihan

Di sana mencapai nilai y = 1 dan kemudian berkurang sampai mencapai nol di π radianes (180 °). Selanjutnya semakin menurun, karena nilainya menjadi negatif sampai mencapai −1 ketika sudut adalah 3π/2 radian (270 °).

Akhirnya, itu meningkat lagi sampai kembali ke nol dalam 360 °, di mana semuanya dimulai lagi. Ini membuat y = sin x a fungsi periodik periode 2π, jadi fungsi sinus tidak bersifat bypective.

Selain itu, grafiknya simetris sehubungan dengan titik (0,0), oleh karena itu fungsinya ganjil.

Kemudian grafik y = sen x:

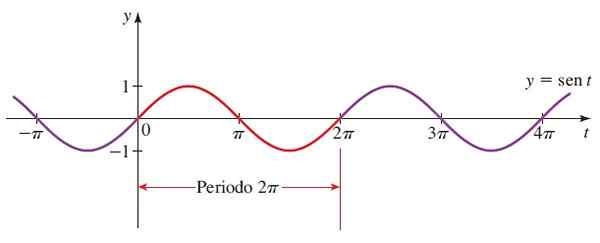Gambar 3. Grafik fungsi f (x) = sin x. Sumber: Stewart, J. PRECCCULMENT: Matematika untuk universitas.

Bagian merah adalah periode pertama. Sudut negatif juga dipertimbangkan, karena jari -jari lingkaran trigonometri dapat berputar dalam jadwal.

Domain sen x = Semua reales.

Sen X Range atau Rute = [-1,1]

Fungsi f (x) = cos x

Pada titik P (1.0) Fungsi coseno bernilai 1 dan dari sana berkurang, mencapai 0 saat sudut π/2. Lanjutkan berkurang dan mengambil nilai negatif, sampai mencapai -1 pada sudut π.

Kemudian mulai meningkat secara bertahap sampai mencapai 0 dalam 3π/2 dan mengambil nilai lagi ketika jari -jari telah berubah menjadi putaran total. Dari sana siklus diulang, karena cos x bersifat periodik dan juga torsi (simetris di sekitar sumbu vertikal).

Bentuk fungsi kosinus sama dengan fungsi sinus, kecuali jika mereka menggeser π/2 yang sehubungan dengan yang lain.

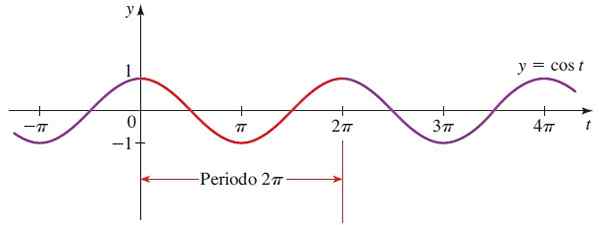Gambar 4. Grafik fungsi f (x) = sin x. Sumber: Stewart, J. PRECCCULMENT: Matematika untuk universitas.

Cos x domain = Semua reales.

Dapat melayani Anda: perkiraan waktu

Rute jangkauan atau cos x = [-1,1]

Fungsi trigonometri terputus -putus

Fungsi TG X, CTG X, SEC X dan HARS. Karena ini bernilai 0 di beberapa sudut, ketika mereka muncul di denominator mereka membuat fungsi terputus.

Dan karena sinus dan kosinus adalah fungsi periodik, fungsi Tg x, CTG X, Sec X, Harm X juga merupakan.

Fungsi garis singgung f (x) = tg x

Untuk fungsi tangen, nilai diskontinuitas adalah: ± π/2, ± 3π/2, ± 5π/2 ... ada fungsi yang mengambil nilai yang sangat besar atau sangat kecil. Secara umum ini terjadi untuk semua kelipatan π dari bentuk (2n+1) π/2, baik positif maupun negatif, dengan n = 0, 1, 2 ..

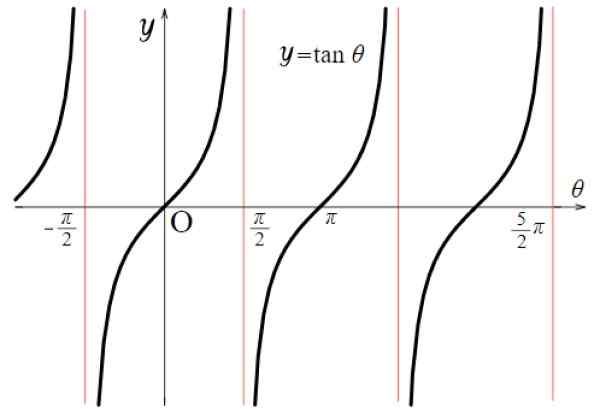Gambar 5. Grafik fungsi f (x) = tg x. Sumber: Wikimedia Commons.

Karena itu:

Domain TG X: D = x ∈ R / x ≠ (2n+1) π/ 2; n ∈ Z

Tur peringkat atau TG x: Semua reales.

Perhatikan bahwa fungsi f (x) = tg x diulang antara - π/2 dan + π/2, oleh karena itu periodenya adalah π. Selain itu, simetris sehubungan dengan asal.

Fungsi cotangent f (x) = ctg x

Untuk fungsi ini, nilai diskontinuitas terjadi pada 0, ± π, ± 2π ..., yaitu, seluruh kelipatan π.

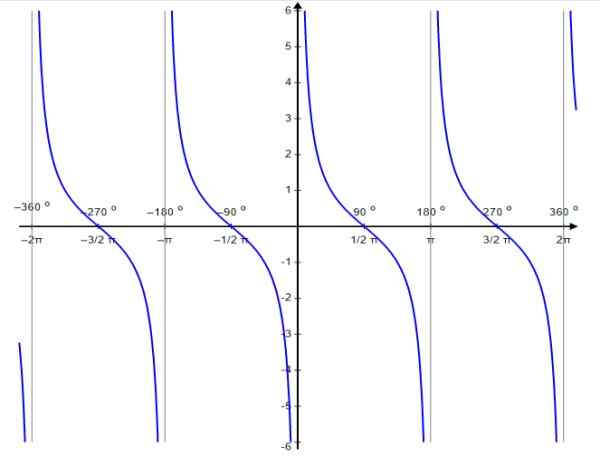Gambar 6. Grafik fungsi f (x) = cotg x. Sumber: Wikimedia Commons.

Seperti fungsi garis singgung, fungsi cotangent adalah periode periodik π. Baginya terpenuhi bahwa:

Domain CTG X: D = x ∈ R / x ≠ n π; n ∈ Z

CTG X Range atau rute: Semua reales.

Fungsi pengeringan f (x) = detik x

Fungsi SEC X memiliki titik diskontinuitas dalam ± π/2, ± 3π/2, ± 5π/2…, di mana cos x = 0. Ini juga periode periodik π dan juga diamati dari grafik bahwa fungsi tidak pernah mengambil nilai dalam interval (-1,1)

Dapat melayani Anda: bilangan bulat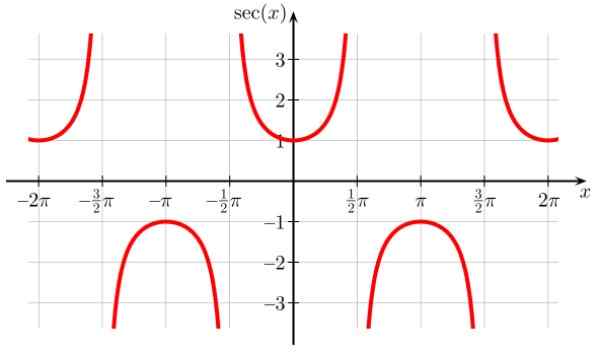 Gambar 7. Grafik fungsi f (x) = sec x. Sumber: Wikimedia Commons.

Doma of Sec X: D = x ∈ R / x ≠ (2n+1) π/ 2; n ∈ Z

Sec X Range atau Rute: Semua reais kecuali (-1,1)

Fungsi panen f (x) = bahaya x

Ini mirip dengan fungsi pengeringan, meskipun dipindahkan ke kanan, oleh karena itu titik diskontinuitas adalah 0, ± π, ± 2π dan seluruh kelipatan π. Itu juga berkala.

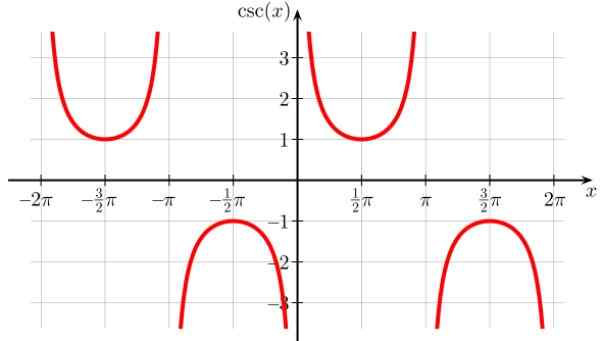Angka 8. Grafik fungsi f (x) = bahaya x. Sumber: Wikimedia Commons. Geek3/cc by-sa (https: // createveCommons.Org/lisensi/by-sa/4.0)

Domain bahaya x: D = x ∈ R / x ≠ n π; n ∈ Z

Kisaran atau Rute Harmoni: Semua reais kecuali (-1,1)

Olahraga diselesaikan

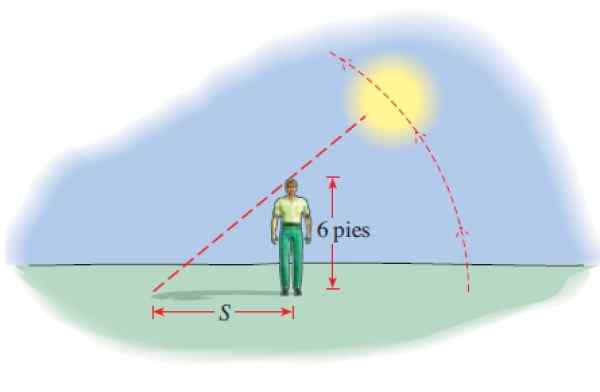
Seorang pria setinggi 6 kaki memproyeksikan naungan yang panjangnya diberikan oleh:

S (t) = 6 │cot (π.T/12) │

Dengan s di kaki dan t jumlah jam setelah jam 6 pagi. Berapa bayangan pada jam 8 pagi, pada 12 m, jam 2 siang dan jam 17:45?

Larutan

Kita harus mengevaluasi fungsi untuk masing -masing nilai yang diberikan, perhatikan bahwa nilai absolut harus diambil, karena panjang bayangan positif:

-Pada jam 8 pagi, 2 jam telah berlalu dari jam 6 pagi, oleh karena itu t = 2 dan s (t) adalah:

S (2) = 6 │cot (π.2/12) │Pies = 6 │cot (π/6) │Pies = 10.39 kaki.

-Ketika 12 N, t = 6 jam telah berlalu, oleh karena itu:

S (6) = 6 │cot (π.6/12) │Pies = 6 │cot (π/2) │pies = 0 kaki. (Pada saat itu matahari jatuh secara vertikal di kepala orang itu).

-Pada jam 2 siang mereka menghabiskan t = 8 jam:

S (8) = 6 │cot (π.8/12) │Pies = 6 │cot (2π /3) │Pies = 3.46 kaki.

-Saat pukul 17:45, 11 telah melewati 11.75 jam dari jam 6 pagi, lalu:

S (11.75) = 6 │cot (π x 11.75/12) │Pies = 91.54 kaki. Saat ini bayangan semakin lama.

Dapatkah pembaca menghitung waktu ketika bayangan orang tersebut sama dengan tinggi badannya?

Referensi

1. Carena, m. 2019. Manual Matematika Preuniversity. Universitas Nasional Pantai.
2. Figuera, J. 1999. Matematika. 1st. Diversifikasi. Edisi Collegiate Bolivarian.
3. Hoffman, J. Pemilihan masalah matematika. Volume 4.
4. Jiménez, r. 2008. Aljabar. Prentice Hall.
5. Zill, d. 1984. Aljabar dan Trigonometri. Bukit McGraw.