Geometri Euclidian

Kami menjelaskan apa geometri Euclidian, sejarahnya, elemen dan kami memberikan beberapa contoh

Euclid dari Alexandria dan elemen -elemennya, oleh Jusepe de Ribera, di sebelah, dua garis non -paralel dan garis yang memotongnya, menggambarkan postulat kelima. Sumber: Wikimedia Commons.

Apa itu geometri Euclidian?

Itu Geometri Euclidian Itu adalah salah satu yang diatur oleh dalil -dalil oleh Euclid de Alejandría, sebuah geometer Yunani yang hidup menuju 300 hingga.C, yang menghormati disiplin ini dinamai, karena itu adalah orang pertama yang mensistematisasikannya.

Cabang matematika ini mempelajari sifat -sifat garis, bidang, sudut dan angka geometris seperti poligon, keliling dan kerucut lainnya. Karenanya pentingnya dalam sains dan teknik, yang pengembangannya mendorong secara signifikan.

Di sisi lain, geometri Euclidean adalah ilmu pasti pertama, karena dengan itu jalur sistematisasi sains dimulai, serta penggunaan logika untuk menunjukkan, dari beberapa aksioma, banyak proposisi yang disebut teorema, untuk menggambarkan sifat -sifat tersebut objek geometris.

Sejarah

Geometri memiliki sejarah panjang, karena minat umat manusia di dalamnya sudah sangat tua dan sumbu pusat geometri Euclidean adalah karya Item, dari Euclid yang bijak dari Alexandria, sebuah kota yang terletak di Mesir, dan yang hidup pada abad keempat hingga.C.

Pada saat itu sifat terpenting dari berbagai tokoh dan badan geometris diketahui. Ada pengetahuan luas tentang geometri, tetapi semuanya empiris dan tidak memiliki sistematisasi.

Kemudian, Raja Mesir Ptoleme dan mempercayakan guru Euclid yang sudah terkenal, yang sekolahnya berada di Alexandria, untuk mengatur semua pengetahuan matematika dan geometris yang tersedia sejauh ini, termasuk teorema dan properti.

Euclides mulai bekerja dan di samping murid -muridnya, menulis elemen karyanya, yang ia bagi menjadi tiga belas buku, sebagai bab. Karya ini akan menjadi referensi untuk geometri untuk generasi mendatang.

Dapat melayani Anda: turunan berturut -turut

Elemen Euclid

Isi elemen diatur sebagai berikut:

• Dalam buku I hingga IV geometri datar berkembang.
• Dalam buku V dan saya melihat teori proporsi.
• Buku IX didedikasikan untuk aritmatika.
• Tidak pahami muncul dalam buku x,
• Geometri Ruang dalam Buku XI hingga XIII.

Geometri Euclidean adalah dasar bagi banyak perkembangan geometris posterior dan saat ini sedang diajarkan di semua sekolah di dunia.

Ini juga memiliki keutamaan menjadi pekerjaan pertama yang memasukkan demonstrasi yang cermat berdasarkan penalaran logis, dan juga dalam memberikan koherensi pada tubuh pengetahuan geometris dan matematika pada waktu itu.

Elemen Dasar Geometri Euclidean

Geometri Euclidean dibangun di sekitar empat elemen dasar, dijelaskan dalam Buku I dari elemen -elemen:

1. Titik
2. Lurus
3. Datar
4. Ruang angkasa

1. Titik

A titik Itu tidak memiliki dimensi atau bagian dan dibedakan dari titik lain hanya dengan lokasinya. Jika dua titik A dan B berbeda, itu karena mereka memiliki posisi yang berbeda, yang ditunjukkan melalui koordinat Cartesian yang terkenal (x, y) jika titik berada di pesawat, atau koordinat (x, y, z) Jika ada di luar angkasa.

Perlu dicatat bahwa sistem Cartesian bukan bagian dari Item dari Euclid, tetapi muncul jauh di kemudian hari dalam 1600 tahun dan disebabkan oleh René Descartes.

2. Lurus

Itu lurus Ini adalah kumpulan titik yang tak terbatas, dan hanya memiliki panjang, bukan lebar. Sebagian darinya biasanya ditarik, dengan panah dalam keduanya menunjukkan bahwa garis berlanjut tanpa batas waktu.

3. Datar

A datar Ini adalah permukaan yang tidak terbatas, sehingga memiliki dua dimensi dan di mana sebagian diwakili, dengan menggunakan persegi atau persegi panjang.

Di sana, di pesawat, ada banyak tokoh geometris, seperti garis, kurva terbuka dan tertutup, antara lain.

Dapat melayani Anda: Persamaan umum garis yang kemiringannya sama dengan 2/3

4. Ruang angkasa

Akhirnya, ada ruang angkasa Dengan tiga dimensinya, mampu menampung semua poin. Itu berisi bidang dan tubuh geometris yang ditandai dengan volumenya, seperti polyhedra, bola dan banyak lagi.

Ini dapat dianggap sebagai definisi dasar geometri Euclidean, tetapi selain itu, Euclides menawarkan sekitar 150 definisi yang bervariasi dalam pekerjaan mereka.

Gagasan umum

Mereka terdiri dari fakta -fakta yang jelas dan intuitif, yang tidak dimiliki dengan baik dari ruang lingkup geometri dan digunakan sebagai konsep berkembang. Mereka merujuk pada "hal -hal" dalam konteks yang sangat luas:

1. Hal -hal yang sama dengan hal lain, mereka sama satu sama lain.
2. Jika hal -hal ditambahkan ke serangkaian hal lain, dan semuanya sama, hasil apa juga sama.
3. Jika hal yang sama dicuri, sisanya juga sama.
4. Ketika hal -hal bertepatan satu sama lain, itu karena mereka sama.
5. Keseluruhan selalu lebih besar dari partai -partai, diambil secara terpisah.

Deposulat geometri Euclidean

Deposulasi atau aksioma adalah pernyataan sederhana yang dianggap benar dan jelas, sehingga tidak memerlukan demonstrasi.

Mereka merupakan dasar geometri Euclidian dan Euclid membentuk lima dalam buku mereka:

1. Jadilah dua titik berbeda ke dan B, hanya ada satu baris yang melewati mereka, yaitu, dua poin menentukan garis.
2. Segmen bujursangkar apa pun dapat diperpanjang tanpa batas waktu untuk membentuk garis, oleh karena itu, setiap segmen milik suatu garis.
3. Jika Anda memiliki dua titik berbeda atau dan A, Anda selalu dapat menggambar lingkaran dengan pusat di O dan jari -jari sama dengan segmen OA.
4. Semua sudut lurus satu sama lain.
5. Diberi garis dan titik P yang bukan miliknya, selalu mungkin.

Postulat terakhir, terutama dalam versi aslinya, tidak terlihat sesederhana yang lain. Itu menyatakan bahwa:

Dapat melayani Anda: heptagon

“Jika garis lurus yang jatuh pada dua garis lain, membuat dua sudut interior di sisi yang sama kurang dari dua sudut lurus, kata garis lurus, meluas tanpa batas waktu, mereka (berpotongan) di sisi tempat sudut kecil itu adalah bahwa dua sudut lurus ".

Yaitu, awalnya postulate 5 menetapkan kondisi sehingga dua baris tidak paralel. Tetapi lebih jelas ketika ditulis sedemikian rupa sehingga menggambarkan sebaliknya, yaitu paralelisme garis.

Contoh geometri Euclidean

Contoh 1

Ada tiga titik berbeda, diberi label dengan huruf A, B dan C.

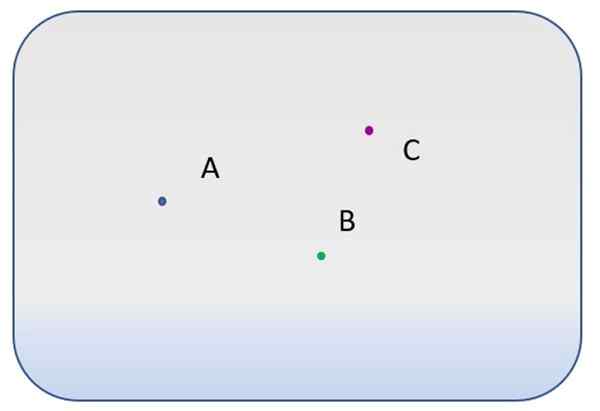
1. Berapa banyak garis yang berbeda melewati titik a?
2. Dan berapa banyak yang dapat ditarik antara titik A dan B? Dan antara A dan C?
3. Apakah mungkin untuk menarik garis ke titik mana A, B dan C?

Menjawab

Menurut postulat I, garis lurus tak terbatas dapat ditarik melalui A, karena dua titik diperlukan untuk menentukan garis.

Jawaban b

Entre a dan b hanya bisa ditarik garis. Dan antara A dan C juga.

Jawaban c

Tidak mungkin satu garis mengandung A, B dan C secara bersamaan.

Contoh 2

Ini diminta untuk membangun langkah demi langkah segitiga sama sisi (semua sisinya sama), mengetahui salah satu sisinya, yang merupakan segmen AB dan menunjukkan dalam setiap langkah postulat atau gagasan umum yang digunakan dalam konstruksi dalam.

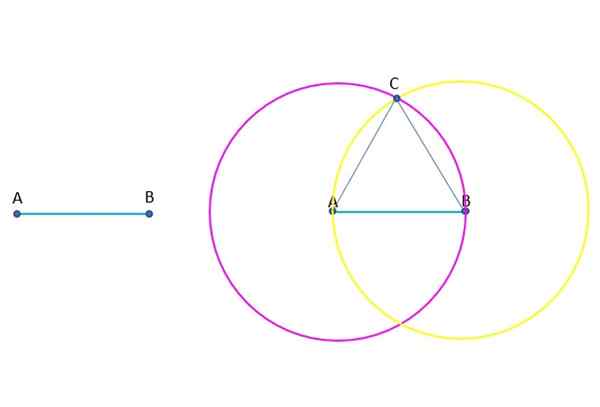Konstruksi segitiga sisi ABC. Sumber: f. Zapata.

Menjawab

Langkah 1

Lingkaran dengan pusat di A dan Radio AB ditarik. Ini selalu mungkin, menurut postulat III.

Langkah 2

Lingkar lain dengan pusat di B dan Radio AB ditarik, dan postulat III diterapkan lagi.

Langkah 3

Kedua keliling, yang memiliki jari -jari yang sama, dipotong pada titik C. Sekarang Anda dapat menggambar segmen yang menyatukan C dengan A dan B masing -masing, menurut postulat I.

Segmen -segmen ini adalah radio dari lingkar dan oleh karena itu ukuran AC dan BC sama dengan AB, menurut Gagasan Umum 1. Maka segitiga ABC adalah hal yang sama.