Properti Heptadecágono, Diagonals, Perimeter, Area

Dia Heptadecágono Ini adalah poligon biasa dari 17 sisi dan 17 simpul. Konstruksinya dapat dilakukan dengan gaya Euclidian, yaitu hanya menggunakan aturan dan kompas. Itu adalah kejeniusan besar matematika Carl Friedrich Gauss (1777-1855), menghitung hanya 18 tahun, yang menemukan prosedur untuk pembangunannya pada 1796. 

Rupanya, Gauss selalu merasa sangat condong ke sosok geometris ini, sampai -sampai sejak hari dia menemukan konstruksinya, dia memutuskan untuk menjadi ahli matematika. Dikatakan juga bahwa dia ingin Heptadecágono direkam di batu nisannya.

Gambar 1. Heptadecágono adalah poligon biasa dari 17 sisi dan 17 simpul. Sumber: f. Zapata.

Gauss juga menemukan formula untuk menentukan poligon reguler mana yang memiliki kemungkinan dibangun dengan aturan dan kompas, karena beberapa tidak memiliki konstruksi Euclidean yang tepat.

[TOC]

Karakteristik Heptadecágono

Adapun karakteristiknya, seperti setiap poligon, jumlah sudut internalnya adalah penting. Dalam poligon biasa N sisi, jumlah diberikan oleh:

SA (n) = (n -2) *180º.

Untuk heptadecágono jumlah sisi N adalah 17, Yang berarti bahwa jumlah sudut internalnya adalah:

SA (17) = (17 - 2) * 180º = 15 * 180º = 2700º.

Jumlah ini, yang diekspresikan dalam Radianes seperti ini:

SA (17) = (17 - 2) * π = 15 * π = 15π

Dari formula sebelumnya dapat dengan mudah disimpulkan bahwa setiap sudut internal heptadecágono memiliki ukuran α yang tepat yang diberikan oleh:

α = 2700º/17 = (15/17) π Radianes

Oleh karena itu sudut internal adalah:

α ≈ 158.824º

Diagonal dan perimeter

Diagonal dan perimeter adalah aspek penting lainnya. Dalam poligon apa pun jumlah diagonal adalah: 

D = n (n - 3) / 2 dan dalam kasus heptadecágono, seperti N = 17, Kamu harus D = 119 Diagonal.

Dapat melayani Anda: trinomial

Di sisi lain, jika panjang masing -masing sisi heptadecágono diketahui, maka perimeter heptadecágon biasa hanya menambahkan 17 kali panjang itu, atau apa yang setara 17 kali panjangnya D Di setiap sisi:

P = 17 d

Perimeter Heptadecágono 

Terkadang hanya radio yang diketahui R dari heptadecágono, jadi perlu untuk mengembangkan formula untuk kasus ini.

Untuk tujuan ini, konsep apothem. Apotheme adalah segmen yang beralih dari pusat poligon biasa ke titik tengah di satu sisi. Apothem relatif ke samping tegak lurus terhadap sisi itu (lihat Gambar 2).

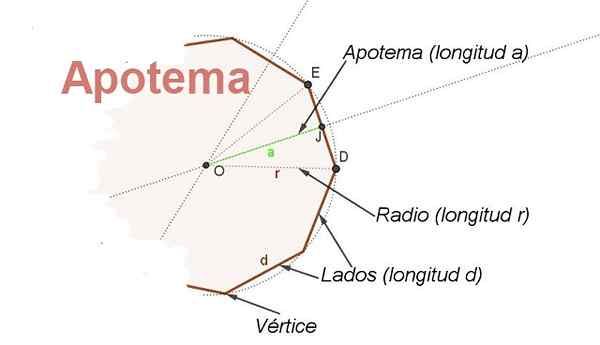Gambar 2. Bagian -bagian dari Radio R Polygon dan Apothemnya ditampilkan. (Elaborasi sendiri)

Selain itu, apothem adalah bisector dari sudut dengan titik tengah dan sisi pada dua simpul berturut -turut poligon, ini memungkinkan untuk menemukan hubungan antara radio R dan sisinya D.

Jika dipanggil β ke sudut tengah Kelinci betina Dan dengan mempertimbangkan apothem itu OJ adalah bisector yang Anda miliki Ex = d/2 = r sen (β/2), di mana Anda memiliki hubungan untuk menemukan panjangnya D di sisi poligon yang diketahui radionya R dan sudut tengahnya β:

D = 2 r sin (β/2)

Dalam kasus heptadecágon β = 360º/17 Untuk apa yang Anda miliki:

D = 2 R Sen (180º/17) ≈ 0,3675 r

Akhirnya, formula perimeter heptadecágono diketahui jari -jari itu diperoleh:

P = 34 R Sen (180º/17) ≈ 6.2475 r

Perimeter heptadecágonon Pcir = 2π r ≈ 6.2832 r.

Daerah

Untuk menentukan area heptadecágono, kami akan merujuk pada Gambar 2, yang menunjukkan sisi dan apothem dari poligon biasa N sisi. Dalam gambar itu segitiga EOD Ini memiliki area yang sama dengan pangkalan D (sisi poligon) dengan tinggi ke (Polygon Apothem) dibagi dengan 2:

Itu dapat melayani Anda: serangkaian kekuatan: contoh dan latihan

Eod = (d x a) / 2

Jadi apothem yang diketahui itu ke dari heptadecágono dan sisi D yang sama adalah:

Area Heptadecágono = (17/2) (d x a)

Area yang diberikan sisi

Untuk mendapatkan formula untuk daerah Heptadecágono mengetahui panjang tujuh belas sisi, perlu untuk mencapai hubungan antara panjang apothem ke dan sisinya D.

Mengacu pada Gambar 2 Anda memiliki hubungan trigonometri berikut:

Tan (β/ 2) = EG/ OJ = (d/ 2)/ a, makhluk β ke sudut tengah Kelinci betina. Sehingga apothem itu ke dapat dihitung jika panjangnya diketahui D dari sisi poligon dan sudut tengah β:

A = (d/2) cotan (β/2)

Jika ungkapan ini untuk apothem diganti sekarang, dalam rumus area Heptadecágono yang diperoleh di bagian sebelumnya, Anda memiliki:

Area Heptadecágono = (17/4) (D²) Cotan (β/2)

Makhluk β = 360º/17 Untuk Heptadecágono, jadi Anda akhirnya memiliki formula yang diinginkan:

Area Heptadecágono = (17/4) (D²) Cotan (180º/17)

Area yang diberikan radio

Pada bagian sebelumnya, hubungan antara sisi D dari poligon biasa dan Radio R -nya telah ditemukan, berikut ini: berikut: berikut ini: berikut ini:

D = 2 r sin (β/2)

Ungkapan ini untuk D Itu dimasukkan ke dalam ekspresi yang diperoleh di bagian sebelumnya untuk area tersebut. Jika substitusi dan penyederhanaan yang relevan dibuat, formula yang memungkinkan untuk menghitung area heptadecágono diperoleh:

Area Heptadecágono = (17/2) (r²) Sin (β) = (17/2) (r²) Sen (360º/17)

Ekspresi perkiraan untuk area tersebut adalah:

Area Heptadecágono = 3.0706 (r²) 

Seperti yang diharapkan, area ini sedikit kurang dari area lingkaran yang dibatasi pada heptadecágon KE_Circ = π r² ≈ 3.1416 r². Lebih tepatnya, 2% lebih rendah dari lingkarannya yang dibatasi.

Dapat melayani Anda: area pentagon biasa dan tidak teratur: bagaimana itu diambil, latihan

Contoh

Contoh 1

Agar heptadecágono memiliki sisi 2 cm, nilai apa yang harus dimiliki oleh jari -jari dan diameter lingkar yang dibatasi? Temukan juga nilai perimeter.

Untuk menjawab pertanyaan, perlu mengingat hubungan antara sisi dan jari -jari poligon reguler dari sisi N:

 D = 2 R Sen (180º / N)

Untuk heptadecágono N = 17, karena itu D = 0,3675 r, Dengan kata lain

Berdiameter 10.8844 cm.

Perimeter heptadecágon sisi 2 cm adalah p = 17* 2 cm = 34 cm.

Contoh 2

Berapa area sisi heptadecágono de 2 cm biasa?

Penting untuk merujuk pada rumus yang ditunjukkan pada bagian sebelumnya, yang memungkinkan untuk menemukan area heptadecágono saat panjangnya D Di pihaknya:

Area Heptadecágono = (17/4) (D²) / Tan (180º / 17) 

Saat mengganti D = 2 cm dalam formula anterior diperoleh:

Daerah = 90,94 cm

Referensi

1. C. DAN. KE. (2003). Elemen Geometri: Dengan Latihan dan Geometri Kompas. Universitas Medellin.
2. Campos, f., Cerecedo, f. J. (2014). Matematika 2. Grup Editorial Patria.
3. Freed, k. (2007). Temukan poligon. Perusahaan Pendidikan Benchmark.
4. Hendrik, v. (2013). Poligon umum. Birkhäuser.
5. Iger. (S.F.). Matematika semester pertama Tacaná. Iger.
6. Jr. Geometri. (2014). Poligon. Lulu Press, Inc.
7. Miller, Heeren, & Hornsby. (2006). Matematika: Penalaran dan Aplikasi (Edisi Kesepuluh). Pendidikan Pearson.
8. Patiño, m. (2006). Matematika 5. Progreso editorial.
9. Sada, m. 17 sisi reguler dengan aturan dan kompas. Pulih dari: geogebra.org
10. Wikipedia. Heptadecágono. Pulih dari: is.Wikipedia.com