Sejarah Trigonometri dari Asalnya

Itu Sejarah Trigonometri Ini mengacu pada serangkaian fakta dan kemajuan yang terjadi di sekitar cabang matematika ini dari asal -usulnya ke peristiwa terbaru.

Saat melakukan perjalanan singkat melalui sejarahnya, terbukti bahwa ilmu ini dilahirkan sebagai tanggapan terhadap masalah yang dihadapi oleh para astronom dan navigator kuno untuk menganalisis perpindahan bintang -bintang di langit.

Istilah ini muncul untuk pertama kalinya dalam buku Trigonometriae Libri Quinque, ditulis oleh ahli matematika dan ilmuwan Jerman Pitiscus Bartolomé (1561-1613). Via Wikimedia Commons.

Demikian juga, kata trigonometri muncul dari komposisi dua kata Yunani: Trigonon (segitiga) dan Metron (cakupan). Istilah ini muncul untuk pertama kalinya dalam buku ini Trigonometriae Libri Quinque, Ditulis oleh matematikawan dan ilmuwan Jerman Pitiscus Bartolomé (1561-1613).

Dengan cara ini, etimologi kata menunjukkan bahwa trigonometri adalah studi hubungan antara sudut segitiga dan segmen atau garis yang membentuknya.

[TOC]

Awal trigonometri

Langkah pertama trigonometri dilakukan oleh manusia ketika dipromosikan oleh kebutuhan untuk mengetahui dan menganalisis pergerakan bintang -bintang.

Artinya, manusia yang dirancang trigonometri karena ditemukan dalam situasi di mana tidak mungkin melakukan pengukuran secara langsung, karena untuk menghitung bintang, diperlukan alat matematika yang lebih kompleks.

- Studi di Babel

Meja lumpur yang ditulis oleh orang -orang Babilonia yang disebut Plimpton 322. Via: Wikimedia Commons

Studi menunjukkan bahwa lebih dari 3 lalu.000 tahun orang Babilonia sudah menangani konsep alasan sudut dan trigonometri, yaitu, mereka mampu membangun hubungan antara sisi dan sudut segitiga.

Misalnya, meja lumpur - ditulis oleh orang -orang Babel - disebut PLIMPTON 322 (1800 a. C.) menunjukkan serangkaian kolom dan baris yang berisi angka dalam penulisan runcing. Menurut penelitian yang dilakukan oleh beberapa ahli, tablet ini mewakili apa yang tampaknya menjadi serangkaian fungsi trigonometri.

Dapat melayani Anda: apa pedomannya? (Geometri)

Orang Babilonia akrab dengan konsep-konsep yang memunculkan teorema Pythagoras (569-474 a.C) dan mereka memahami prinsip mereka.

Dengan cara yang sama, mereka juga tahu teorema yang dikaitkan dengan Thales of Miletus (695-546.C), yang menunjukkan bahwa setiap lurus, ditarik sejajar dengan sisi segitiga, terbentuk dengan dua sisi lain segitiga lain yang mirip dengan segitiga awal.

- Orang Mesir Kuno

Orang Mesir kuno berhasil mempertahankan lereng secara seragam pada masing -masing wajah piramida. Via: Pixabay

Meskipun tidak tepat untuk berbicara tentang trigonometri dalam bidang umum matematika Mesir, tidak ada keraguan bahwa peradaban ini menangani konsep trigonometri tertentu.

Ini terjadi karena ketika merenungkan bangunan -bangunan besar yang dibuat oleh orang Mesir, seperti piramida, dapat disimpulkan bahwa mereka memiliki pengetahuan tentang trigonometri.

Kesulitan teknik dasar yang dihadapi oleh orang Mesir - dan itu sembuh luar biasa.

Untuk ini mereka menggunakan konsep yang mereka sebut "seqt" dan itu setara dengan apa yang kita pahami hari ini sebagai kemiringan permukaan datar yang cenderung.

Selain itu, orang Mesir untuk melakukan pengukuran pada permukaan vertikal yang digunakan sebagai unit "siku" dan di horizontal "tangan", yang sesuai dengan 1/7 dari siku. Dengan cara ini mereka menghitung seqt atau tertunda di bangunan yang berbeda. Misalnya, di piramida jufú (queope) seqt adalah 5 1/2 tangan per siku.

- Yunani kuno dan tabel string

Semua pengetahuan tentang orang Babilonia dan Mesir kuno diteruskan ke Yunani, di mana ahli matematika dan astronom Nicea (190-120 disorot (190-120. C), yang dianggap sebagai bapak trigonometri. Hiparco menciptakan tabel "string", yang dengannya ia berhasil menyelesaikan masalah segitiga datar.

Nicea hiparco - sumber: ditransfer dari.Wikipedia ke Commons oleh Maksim - di bawah domain publik

Untuk membuatnya, menggunakan keliling dengan jari -jari tertentu (jari -jari adalah jarak antara pusat lingkaran dan titik lingkaran apa pun).

Dapat melayani Anda: probabilitas bersyarat: rumus dan persamaan, sifat, contoh

Kemudian, itu menggusur jari -jari untuk mendefinisikan sudut yang berbeda; Saat melakukan ini menunjuk pada meja, panjang garis yang dibatasi pada sisi sudut dan keliling.

"String" ini ternyata adalah prekursor tabel fungsi trigonometri yang kita gunakan saat ini.

- Kontribusi India

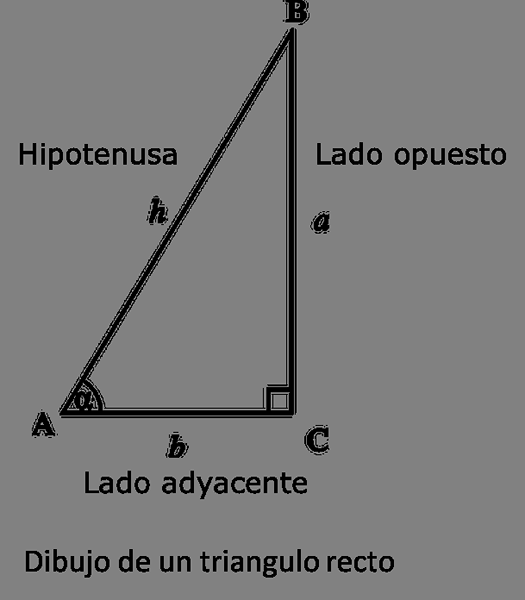Menggambar segitiga kanan.

Seperti para sarjana Yunani, para astronom di India juga mengembangkan sistem trigonometri, tetapi tidak seperti orang -orang Yunani para astronom ini mendasarkan analisis mereka pada fungsi "sinus" alih -alih menggunakan string.

Namun, fungsi "sinus" yang diekspresikan oleh para astronom ini bukan yang digunakan saat ini; Fungsi ini bukan proporsi (seperti yang digunakan saat ini), tetapi panjang sisi yang berlawanan dengan sudut segitiga persegi panjang yang diketahui hipotenus yang diketahui.

- Fungsi Arab dan Trigonometri

Pada akhir abad kedelapan, para astronom Arab, dipengaruhi oleh studi trigonometri yang dilakukan oleh orang -orang Yunani dan India, memulai studi penting tentang hubungan antara sudut dan sisi mereka.

Dengan cara ini, pada akhir abad ke -10 mereka mengangkat fungsi payudara, kosinus, garis singgung, cotangent, pengeringan, dan pemanen yang terkenal.

Mereka juga menemukan dan memverifikasi teorema trigonometri primer, yang digunakan dalam analisis segitiga datar dan bola. Selain itu, ahli matematika Arab menyarankan penggunaan satu nilai ("1") untuk radio (r = 1), yang memunculkan nilai -nilai modern fungsi trigonometri.

- Kontribusi dari barat

Johann Müller yang dikenal sebagai Regiomontanus (1436-1476). Sistematisasi yang dicapai dan generalisasi metode trigonometri yang digunakan di area geometri. Via: Wikimedia Commons

Matematika Barat, khususnya antara abad kedua belas dan kelima belas, sangat dipengaruhi oleh dalil -dalil Yunani kuno, India dan orang Arab.

Dapat melayani Anda: chi-square (χ²): distribusi, bagaimana itu dihitung, contoh

Selama waktu ini mereka menentukan di bidang trigonometri-kontribusi Johann Müller, juga dikenal sebagai Regiomontanus (1436-1476). Matematikawan ini mencapai sistematisasi dan generalisasi metode trigonometri yang digunakan di area geometri.

Regiomontanus menguraikan dan menerbitkan perjanjian yang ia sebut Dari Triangulis Omnimodis Libri Quinque, yang terdiri dari lima buku dan total 131 halaman.

Dalam buku ini ia mengatur semua konsep trigonometri datar dan bola, yang kemudian digunakan oleh para astronom penting seperti: Nicolás Copernic.

- Trigonometri abad ketujuh belas dan kedelapan belas

Selama abad ketujuh belas, studi tentang perhitungan trigonometri makmur berkat kontribusi matematikawan seperti Scotch John Napier (1550-1617), yang mengumpulkan berbagai metode untuk resolusi segitiga bola bola bola.

John Napier. Sumber: oleh Encard oleh Samuel Freeman (1773-1857) [domain publik], melalui Wikimedia Common

Belakangan, pada abad ke-18, kontribusi ahli matematika Swiss Leonhard Euler (1707-1783) adalah penentu, karena studinya meletakkan dasar trigonometri modern dengan memperkenalkan notasi yang saat ini digunakan untuk fungsi trigonometri trigonometrik.

Selain itu, Euler berhasil mendefinisikan fungsi eksponensial dan menemukan hubungannya dengan fungsi trigonometri, yang memungkinkannya untuk menggambarkan karakteristik trigonometri.

Selanjutnya, Sir Isaac Newton (1643-1727), dengan menciptakan kalkulus diferensial dan integral, memfasilitasi representasi sejumlah besar fungsi matematika, di antaranya merupakan trigonometri. Dengan cara ini, trigonometri menjadi bagian dari analisis matematika, di mana saat ini memainkan peran mendasar.

Ilustrasi Sir Isaac Newton

Referensi

1. Mansfield, Daniel. Wildberger, n. (2017). PLIMPTON 322 adalah trigonometri seksik Babel yang tepat. Diperoleh pada 20 Mei 2020 dari: Scientedirect.com
2. Jimenez s. (2017). Sejarah trigonometri dan aplikasinya. Diperoleh pada 23 Mei 2020 Deedu
3. Pérez, v. (2010). Sejarah Trigonometri. Diperoleh pada 22 Mei 2020 dari: Laguia2000.com
4. S.KE. (S.F.) Trigonometri. Diperoleh pada 23 Mei 2020 dari: Blogspot.com
5. Merlet, Jean-Pierre (2004). Catatan tentang Sejarah Fungsi Trigonometri. Diperoleh pada 22 Mei 2020 dari: net
6. Adamek, t., Penkalski, k., Valentine, g. (2005). Sejarah Trigonometri. Diperoleh pada 23 Mei 2020 dari: Citssesex.Ist.PSU.Edu/