Icosagono

Apa itu icogon?

A Icosagono atau isodecagon Itu adalah poligon yang memiliki 20 sisi. Poligon adalah sosok datar yang dibentuk oleh urutan terbatas dari segmen garis (lebih dari dua), yang melampirkan daerah bidang.

Setiap segmen garis disebut sisi dan persimpangan setiap pasangan sisi disebut verteks. Menurut jumlah sisi, poligon menerima nama tertentu.

Yang paling umum adalah segitiga, segi empat, pentagon dan segi enam, yang masing -masing memiliki 3, 4, 5, dan 6 sisi, tetapi dapat dibangun dengan jumlah sisi yang diinginkan.

Karakteristik icogon

Di bawah ini adalah beberapa karakteristik poligon dan aplikasinya di icogon.

1- Klasifikasi

Icosgono, sebagai poligon, dapat diklasifikasikan sebagai reguler dan tidak teratur, di mana kata biasa mengacu pada fakta bahwa semua sisi memiliki panjang dan sudut interior yang sama mengukur semuanya sama; Kalau tidak, dikatakan bahwa Icosagon (Polygon) tidak teratur.

2- isodecagon

Icosgon reguler juga disebut isodogone biasa, karena untuk mendapatkan icosgon reguler -gauge yang harus dilakukan adalah bisecar (membagi menjadi dua bagian yang sama) setiap sisi decagon biasa (10 sisi poligon).

3- Perimeter

Untuk menghitung perimeter "P" dari poligon biasa, jumlah sisi dikalikan dengan panjang masing -masing sisi.

Dalam kasus tertentu dari sebuah icogon, perimeter sama dengan 20XL, di mana "l" adalah panjang masing -masing sisi.

Misalnya, jika Anda memiliki Icosagon sisi 3 cm biasa, perimeternya sama dengan 20x3cm = 60 cm.

Jelas bahwa, jika isokagon tidak teratur, formula sebelumnya tidak dapat diterapkan.

Dalam hal ini, 20 sisi harus ditambahkan secara terpisah untuk mendapatkan perimeter, yaitu, perimeter "p" sama dengan ∑li, dengan i = 1.2,…, 20.

4- Diagonal

Jumlah diagonal "D" yang memiliki poligon sama dengan N (n-3)/2, di mana n mewakili jumlah sisi.

Dalam kasus icogon, harus d = 20x (17)/2 = 170 diagonal.

5- jumlah sudut internal

Ada formula yang membantu menghitung jumlah sudut internal poligon biasa, yang dapat diterapkan pada ikosgon biasa.

Formulanya terdiri dari pengurangan 2 dengan jumlah sisi poligon dan kemudian mengalikan angka ini dengan 180º.

Cara rumus ini diperoleh adalah bahwa kita dapat membagi poligon sisi N menjadi segitiga N-2, dan menggunakan fakta bahwa jumlah sudut internal segitiga adalah 180º Formula diperoleh.

Pada gambar berikut, rumus untuk enegon reguler (9 -sided polygon) diilustrasikan.

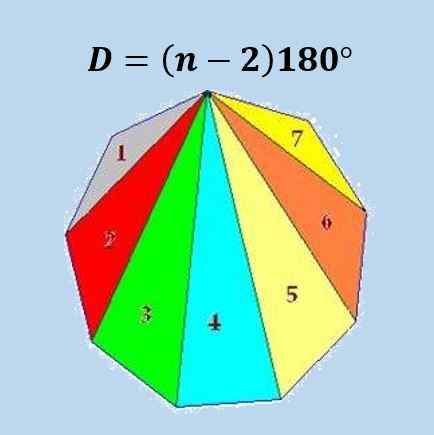
Menggunakan rumus anterior, diperoleh bahwa jumlah sudut internal ikosagon adalah 18 × 180º = 3240º atau 18π.

6- Area

Untuk menghitung area poligon biasa, sangat berguna untuk mengetahui konsep apotheme. Apotheme adalah garis tegak lurus yang bergerak dari pusat poligon biasa ke titik tengah dari salah satu sisinya.

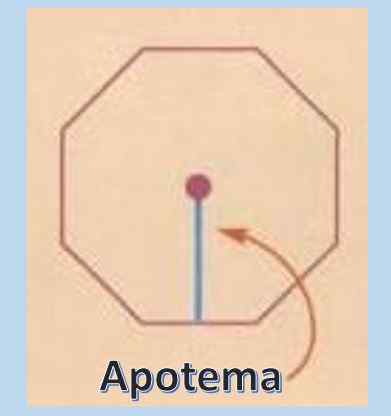
Setelah panjang apothem diketahui, luas poligon biasa adalah A = PXA/2, di mana "p" mewakili perimeter dan "a" apotheme.

Dalam hal Icosagon biasa Anda harus ke daerah Anda adalah A = 20XLXA/2 = 10XLXA, di mana "L" adalah panjang masing -masing sisi dan "A" apotheme -nya.

Di sisi lain, jika Anda memiliki poligon yang tidak beraturan dari sisi N, untuk menghitung luasnya, poligon dibagi menjadi segitiga N-2 yang diketahui, maka area masing-masing segitiga N-2 ini dihitung dan akhirnya semua ini ditambahkan area.

Metode yang dijelaskan di atas dikenal sebagai triangulasi poligon.

Referensi

1. Elemen Geometri: Dengan banyak latihan dan geometri kompas. Universitas Medellin.
2. Iger. (S.F.). Matematika semester pertama Tacaná. Iger.