Demonstrasi Identitas Pythagoras, Contoh, Latihan

Adalah Identitas Pythagoras Semua persamaan trigonometri yang dipenuhi untuk nilai sudut apa pun dan didasarkan pada teorema Pythagoras. Identitas Pythagoras yang paling terkenal adalah identitas trigonometri mendasar:

Sen²(α) + cos²(α) = 1

Gambar 1. Identitas trigonometri Pythagoras.

Ini masih penting dan menggunakan identitas Pythagoras dari garis singgung dan Secant:

Jadi²(α) + 1 = detik²(α)

Dan identitas trigonometri Pythagoras yang melibatkan cotangent dan pemanen:

1 + CTG²(α) = CSC²(α)

[TOC]

Demonstrasi

Alasan trigonometri dada Dan kosinus Mereka diwakili dalam lingkar jari -jari satu (1) yang dikenal sebagai lingkaran trigonometri. Lingkaran ini memiliki pusat di asal koordinat atau.

Sudut diukur dari semi -sumbu positif x, misalnya sudut α pada Gambar 2 (lihat nanti). Bertentangan dengan tangan jam jika sudutnya positif, dan ke arah tangan jika itu adalah sudut negatif.

Semi -right dengan asal atau dan sudut α ditarik, yang mencegat lingkaran unit pada titik p. Titik P diproyeksikan secara ortogonal pada sumbu horizontal X sehingga menimbulkan titik C. Demikian pula P diproyeksikan secara tegak lurus pada sumbu vertikal dan menimbulkan titik S.

Anda memiliki segitiga OCP yang tepat di C. 

Payudara dan kosinus

Harus diingat bahwa alasan trigonometri dada Itu didefinisikan pada segitiga siku -siku sebagai berikut:

Bosom dari sudut segitiga adalah rasio atau rasio antara cateto yang bertentangan dengan sudut dan hipotenus dari segitiga.

Diterapkan pada segitiga OCP dari Gambar 2 akan seperti ini:

Sin (α) = cp / op

Tetapi cp = os dan op = 1, sehingga:

Sin (α) = os

Yang berarti bahwa proyeksi pada sumbu y memiliki nilai yang sama dengan dada sudut yang ditunjukkan. Perlu dicatat bahwa nilai maksimum payudara sudut (+1) terjadi ketika α = 90º dan minimum (-1) ketika α = -90º atau α = 270º.

Dapat melayani Anda: ruang vektor: basis dan dimensi, aksioma, properti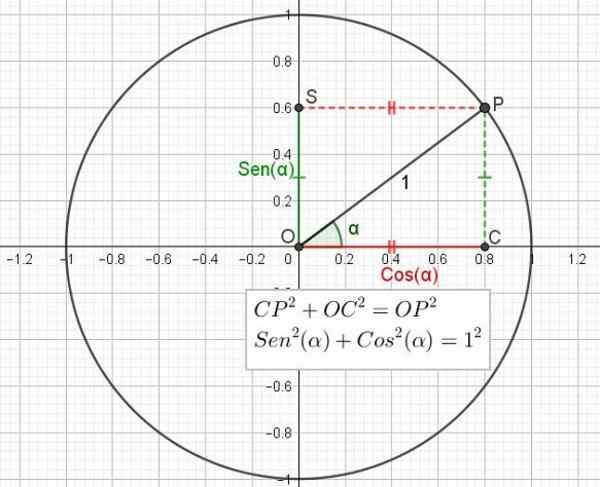Gambar 2. Lingkaran trigonometri yang menunjukkan hubungan antara teorema Pythagoras dan identitas trigonometri fundamental. (Elaborasi sendiri)

Demikian pula, cosinus sudut adalah rasio antara kategori yang berdekatan dengan sudut dan hipotenus dari segitiga.

Diterapkan pada segitiga OCP dari Gambar 2 akan seperti ini:

Cos (α) = oc / op

Tapi op = 1, jadi itu:

Cos (α) = oc

Yang berarti bahwa proyeksi OC pada sumbu x memiliki nilai yang sama dengan dada sudut yang ditunjukkan. Perlu dicatat bahwa nilai maksimum cosinus (+1) terjadi ketika α = 0º atau α = 360º, sedangkan nilai minimum cosinus adalah (-1) ketika α = 180º.

Identitas mendasar

Untuk segitiga OCP persegi panjang, teorema Pythagoras diterapkan, yang menyatakan bahwa jumlah kuadrat kategori sama dengan kuadrat hipotenus:

Cp² + Oc² = Op²

Tetapi telah dikatakan bahwa cp = os = sin (α), bahwa oc = cos (α) dan bahwa op = 1, sehingga ekspresi sebelumnya dapat ditulis ulang tergantung pada sinus dan kosinus sudut:

Sen²(α) + cos²(α) = 1

Sumbu Tangen

Sama seperti sumbu x dalam lingkaran trigonometri adalah sumbu kosinus dan sumbu dan sumbu payudara, dengan cara yang sama ada sumbu garis singgung (lihat Gambar 3) yang justru garis singgung ke unit pada unit Lingkaran di titik pada titik B koordinat (1, 0). 

Jika Anda ingin mengetahui nilai garis singgung sudut, sudut diambil dari semi -abs positif x, persimpangan sudut dengan sumbu garis singgung menentukan titik Q, panjang segmen OQ adalah garis singgung sudut.

Dapat melayani Anda: turunan aljabar

Ini karena menurut definisi, garis singgung sudut α adalah Cateto QB yang berlawanan antara Cateto OB yang berdekatan. Artinya begitu (α) = qb / ob = qb / 1 = qb.

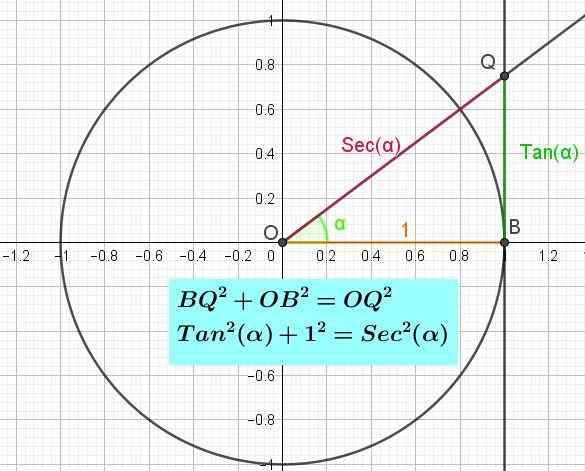Gambar 3. Lingkaran trigonometri menunjukkan sumbu garis singgung dan identitas Pythagoras. (Elaborasi sendiri)

Identitas Pythagoras

Identitas Pythagoras dari garis singgung dapat ditunjukkan jika segitiga persegi panjang dalam B (Gambar 3) dipertimbangkan (Gambar 3). Menerapkan Teorema Pythagoras untuk Segitiga Kata Anda harus bq² + Ob² = Oq². Tetapi telah dikatakan bahwa bq = tan (α), bahwa ob = 1 dan bahwa oq = detik (α), sehingga mengganti dalam kesetaraan pythagoras untuk segitiga kanan OBQ yang dimilikinya:

Jadi²(α) + 1 = detik²(α).

Contoh

Verifikasi apakah identitas Pythagoras dipenuhi dalam segitiga persegi panjang Catetos AB = 4 dan BC = 3.

Solusi: Kategori diketahui, perlu untuk menentukan hipotenus, yaitu:

Ac = √ (ab^2 + bc^2) = √ (4^2 + 3^2) = √ (16 + 9) = √ (25) = 5.

Sudut ∡BAC akan disebut α, ∡BAC = α. Sekarang alasan trigonometri ditentukan:

Sin α = bc / ac = 3/5 

Cos α = ab / ac = 4/5 

Tan α = bc / ab = 3/4 

Cotan α = AB / BC = 4/3 

Dt α = ac / ab = 5/4 

CSC α = AC / BC = 5/3

Itu dimulai dengan identitas trigonometri fundamental:

Sen²(α) + cos²(α) = 1

(3/5)^2 + (4/5)^2 = 9/25 + 16/25 = (9 +16)/25 = 25/25 = 1

Disimpulkan bahwa itu terpenuhi.

- Identitas Pythagoras berikutnya adalah singgung:

Jadi²(α) + 1 = detik²(α)

(3/4)^2 + 1 = 9/16 + 16/16 = (9 + 16)/16 = 25/16 = (5/4)^2

Dan disimpulkan bahwa identitas garis singgung diverifikasi.

- Demikian pula dari Cotangent:

Dapat melayani Anda: pilihan acak dengan atau tanpa penggantian

1 + CTG²(α) = CSC²(α)

1+ (4/3)^2 = 1 + 16/9 = 25/9 = (5/3)^2

Disimpulkan bahwa itu juga terpenuhi, yang telah menyelesaikan tugas memverifikasi identitas Pythagoras untuk segitiga yang diberikan.

Latihan terpecahkan

Uji identitas berikut, berdasarkan definisi alasan trigonometri dan identitas pytagoric.

Latihan 1

Buktikan apa cos² x = (1 + sen x) (1 - sin x).

Larutan: Anggota yang tepat mengakui produk terkenal dari perkalian binomial dengan konjugatnya yang, seperti yang diketahui, adalah perbedaan kotak:

Cos² x = 1² - Sen² X

Kemudian istilah dengan payudara di sisi kanan melewati ke sisi kiri dengan tanda yang diubah:

Cos² X + sen² x = 1

Mencatat bahwa identitas trigonometri mendasar telah tercapai, jadi disimpulkan bahwa ekspresi yang diberikan adalah identitas, yaitu, dipenuhi untuk nilai x apa pun.

Latihan 2

Mulai dari identitas trigonometri mendasar dan menggunakan definisi alasan trigonometri untuk menunjukkan identitas Pythagoras dari pemanen.

Solusi: Identitas mendasar adalah:

Sen²(x) + cos²(x) = 1

Kedua anggota dibagi antara sen²(x) dan penyebut didistribusikan pada anggota pertama:

Sen²(x)/dosa²(x) + cos²(x)/dosa²(x) = 1/sen²(X)

Itu disederhanakan:

1 + (cos (x)/sen (x))^2 = (1/sin (x))^2

Cos (x)/sin (x) = cotan (x) adalah identitas (non -pythagoras) yang diverifikasi oleh definisi alasan trigonometri. Dengan cara yang sama terjadi dengan identitas berikut: 1/dosa (x) = CSC (x).

Akhirnya Anda harus:

1 + CTG²(x) = CSC²(X)

Referensi

1. Baldor J. (1973). Geometri datar dan ruang dengan pengantar trigonometri. Budaya Amerika Tengah. C.KE.
2. C. DAN. KE. (2003). Elemen Geometri: Dengan Latihan dan Geometri Kompas. Universitas Medellin.
3. Campos, f., Cerecedo, f. J. (2014). Matematika 2. Grup Editorial Patria.
4. Iger. (S.F.). Matematika semester pertama Tacaná. Iger.
5. Jr. Geometri. (2014). Poligon. Lulu Press, Inc.
6. Miller, Heeren, & Hornsby. (2006). Matematika: Penalaran dan Aplikasi (Edisi Kesepuluh). Pendidikan Pearson.
7. Patiño, m. (2006). Matematika 5. Progreso editorial.
8. Wikipedia. Identitas dan formula trigonometri. Pulih dari: is.Wikipedia.com