Kesetaraan matematika
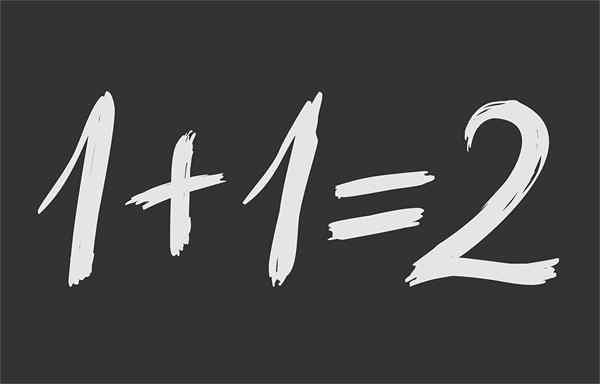
- 4775
- 871
- Tommie Smith
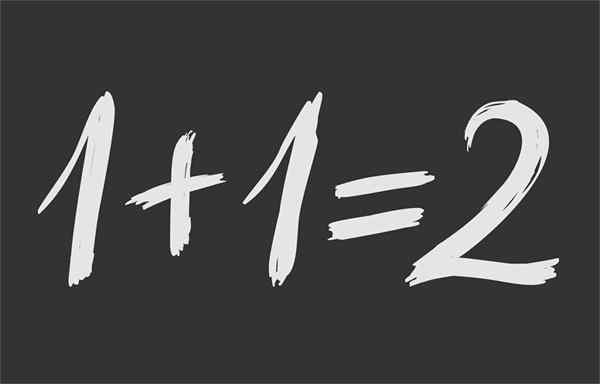 Gambar 1.- Kesetaraan matematika memastikan bahwa 1 + 1 sama 2
Gambar 1.- Kesetaraan matematika memastikan bahwa 1 + 1 sama 2 Apa itu kesetaraan matematika?
Kesetaraan matematika memastikan bahwa dua ekspresi sama atau berbeda, mereka benar -benar setara. Ekspresi ini dapat beragam sifat, misalnya angka, huruf yang melambangkan jumlah atau besaran, kombinasi angka dan huruf, matriks dan banyak lagi.
Simbol yang digunakan untuk menunjukkan kesetaraan dalam bahasa matematika adalah dari dua garis paralel dan horizontal, yang dalam teks cetak adalah simbol yang diketahui dengan baik "=". Misalnya, jika Anda memiliki tiga apel, Anda dapat menulis kesetaraan berikut:
Jumlah apel = 3
Ungkapan "jumlah apel" adalah anggota kiri dan nomor 3 adalah anggota di sebelah kanan kesetaraan.
Karena dimungkinkan untuk menulis jumlah numerik dengan berbagai cara, kesetaraan digunakan untuk menunjukkannya. Mengambil kasus tertentu untuk menggambarkan intinya, ada beberapa cara untuk menulis angka 4, terlepas dari yang paling jelas yaitu 4 = 4, berikut ini dapat ditulis, melalui kesetaraan matematika:
2 + 2 = 4
6 - 2 = 4
8 ÷ 2 = 4
2 × 2 = 4
22 = 4
Kesetaraan yang ditampilkan di sini benar, tetapi kesetaraan mungkin tidak, misalnya 10 + 5 = 20 adalah salah, karena 10 + 5 = 15.
Tentunya pembaca tahu cara lain untuk menulis nomor 4. Perhatikan bahwa ekspresi di setiap sisi kesetaraan dapat berupa angka, kata, huruf yang melambangkan jumlah atau simbol lainnya, misalnya:
x + 1 = 7
ke2B - 1 = xy
f (x) = 2x2
Matematikawan tidak selalu menggunakan simbol kesetaraan, jadi perjanjian matematika lama sangat luas.
Ini dikaitkan dengan ahli matematika dan dokter Robert Remember (1510-1558), lahir di Wales, penciptaan simbol kesetaraan "=", sangat akrab bagi semua hari ini. Ingat, rupanya lelah menulis setiap saat frasa "sama seperti" dalam salah satu perjanjian matematika, ia memutuskan untuk menyingkat di tempatnya para kerabat paralel garis -garis.
Dapat melayani Anda: prisma pentagonal: karakteristik, bagian, simpul, tepi, volumeSifat kesetaraan matematika
Properti berikut memungkinkan bekerja dengan benar dengan kesetaraan matematika. Mereka aksiomatik, jadi mereka tidak memerlukan demonstrasi:
1.- Properti reflektif
Properti ini menetapkan bahwa jumlah berapa pun sama dengan dirinya sendiri. Secara khusus, karena angka apa pun sama dengan dirinya sendiri, yang sama dapat ditulis:
5 = 5
36.35 = 36.35
Jika sejumlah literal, atau kombinasi huruf dan angka, itu juga sama dengan dirinya sendiri:
3x = 3x
ke2Bc-1 = a2Bc-1
2.- Properti simetri
Jumlah atau anggota di kedua sisi kesetaraan dapat ditukar tanpa kehilangan validitas. Yaitu, jika apa yang ada di sebelah kiri simbol "=" ditulis di sebelah kanan Anda, dan apa yang ada di sebelah kanan Anda ditempatkan di sebelah kiri, itu adalah kesetaraan yang sama.
Misalnya, ekspresi 5 + 2 = 7 setara dengan yang satu ini: 7 = 5 + 2. Di jalan yang sama:
12 + 8 = 20; 20 = 12 + 8
x + 1 = 3; 3 = x + 1
x - z = y; y = x - z
3.- Properti Transitif
Properti ini mengacu pada kesetaraan kesetaraan. Jika dua kesetaraan memiliki anggota umum, maka mereka juga sama, karena secara umum:
Jika "x = y" dan "y = z" maka x = z
Untuk mengilustrasikan properti ini, pertimbangkan dua kesetaraan numerik ini: 2 + 2 = 4 dan 6 - 2 = 4. Karena keduanya sama dengan 4 (mereka memiliki anggota umum), maka berikut ini dapat ditulis, tanpa kehilangan validitas apa pun:
2 + 2 = 6 - 2
Contoh lain, kali ini dengan huruf:
Ya x + 1 = 5
DAN
A - b = 5
Jadi:
x+1 = a - b
4.- Properti Pembatalan
Kesetaraan tidak diubah jika pada kedua anggota ada jumlah yang sama yang menambahkan (atau mengurangi) dan diputuskan untuk menghilangkan atau membatalkan ini. Ini adalah properti pembatalan dari jumlah tersebut.
Ambil contoh kesetaraan numerik berikut di mana 10 muncul baik di anggota kanan maupun yang di sebelah kiri:
Ini dapat melayani Anda: Fungsi Trigonometri: Dasar, di bidang Cartesian, Contoh, Latihan2 + 2 + 10 = 6 - 2 + 10
Angka 10 dapat dibatalkan tanpa kesetaraan kehilangan validitasnya, meninggalkan kesetaraan lain yang lebih pendek dan setara dengan yang sebelumnya:
2 + 2 = 6 - 2
Dalam kesetaraan (10 ÷ 2) - 3 = 5 - 3 Integer - 3 milik kedua anggota kesetaraan dan muncul sebagai penambahan, oleh karena itu dapat dibatalkan, memperoleh:
10 ÷ 2 = 5
Itu juga terjadi dengan jumlah literal, misalnya:
Ya x + 2y + z = −A + b + z
Maka "z" dapat dibatalkan, karena ditemukan di kedua sisi kesetaraan sebagai menambahkan (dan dengan tanda yang sama).
Dengan melakukan itu hasilnya:
x + 2y = −a + b
Itu juga dapat menentukan sifat pembatalan perkalian. Jika jumlah yang sama c melipatgandakan kedua anggota kesetaraan, jumlah ini dapat dibatalkan, misalnya:
Cx = cy
Maka C dapat dibatalkan untuk mendapatkan:
x = y
5.- Properti Keseragaman
Kesetaraan tetap tidak berubah -ubah dengan menambahkan, mengurangi, mengalikan atau membagi dengan jumlah yang sama di kedua sisi yang sama.
Misalnya, ia harus 8 + 5 = 13, jika kedua anggota dikalikan dengan angka sewenang -wenang c = 2, kesetaraan tetap:
(8+5) × 2 = 13 × 2
13 × 2 = 26
Kelas setara matematika
Ada berbagai jenis kesetaraan matematika, sehingga mereka diklasifikasikan untuk pemahaman terbaik mereka di:
-Identitas, Mereka adalah kesetaraan di mana kedua anggota itu identik:
2 = 2
x = x
2x = x + x
dan seterusnya.
-Persamaan, Ini adalah persamaan di mana satu atau lebih tidak diketahui muncul, dan benar untuk nilai -nilai tertentu, yaitu, kesetaraan tidak dipenuhi untuk nilai sewenang -wenang, sehingga mereka juga dikenal sebagai kesetaraan bersyarat. Contoh:
x + 1 = 5
X3 = 27
A + b = 40
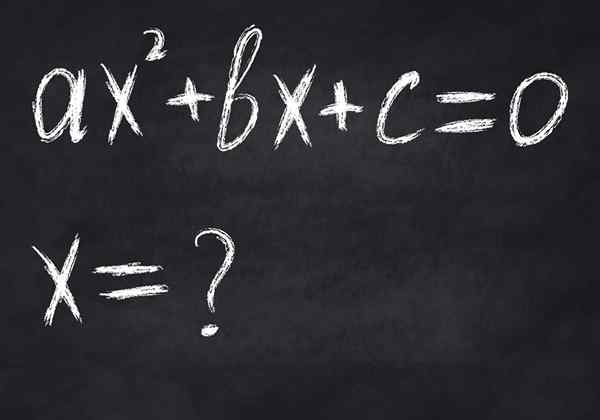 Gambar 2.- Persamaan adalah kesetaraan matematika bersyarat, karena hanya dipenuhi untuk nilai variabel tertentu. Gambar menunjukkan persamaan tingkat kedua, yang paling banyak memiliki dua solusi nyata
Gambar 2.- Persamaan adalah kesetaraan matematika bersyarat, karena hanya dipenuhi untuk nilai variabel tertentu. Gambar menunjukkan persamaan tingkat kedua, yang paling banyak memiliki dua solusi nyata -Kesetaraan, Di dalamnya anggota kiri setara dengan yang di sebelah kanan, bahkan jika mereka tidak sama, misalnya dalam: 23 = 8.
Dapat melayani Anda: prinsip aditif-Rumus, Ini adalah kesetaraan yang selalu dipenuhi untuk nilai -nilai variabel independen, seperti pada rumus yang diketahui dengan baik untuk jarak D tergantung pada waktu T ponsel dengan gerakan bujursangkar yang seragam: D = v ∙ t
Latihan terpecahkan
Latihan 1
Tulis angka 10 hingga empat kesetaraan yang berbeda dan setara.
Larutan
Semua kesetaraan ini mengekspresikan angka 10, tetapi dengan cara yang berbeda:
5 × 2 = 10
11-1 = 10
101= 10
20 ÷ 2 = 10
Latihan 2
Berapa nilai x yang memenuhi kesetaraan x + 1 = 3?
Larutan
Kesetaraan ini adalah persamaan, karena nilai x tidak diketahui. Menggunakan properti 5, jika ekspresi x + 1 = 3 ditambahkan (−1) di kedua sisi simbol "=", kesetaraan tetap:
x + 1 + (−1) = 3 + ( - 1)
Saat menambahkan (−1) ke anggota kiri dan operasi diselesaikan, "X" sendirian di sisi kiri kesetaraan, prosedur ini disebut izin:
x + 1 - 1 = 3−1
x = 2
Oleh karena itu, nilai yang memenuhi kesetaraan ini adalah x = 2.
Latihan 3
Jika ponsel dengan gerakan bujursangkar yang seragam memiliki kecepatan 2.5 m/s, berapa jarak yang berjalan setelah 3 detik?
Larutan
Formula yang terlihat di bagian sebelumnya digunakan, D = v ∙ t, di mana nilai v diganti:
D = 2.5 ∙ t
Ekspresi menjadi kesetaraan ketika t = 3 detik dan operasi diselesaikan:
D = 2.5 ∙ 3 m = 7.5m
Yang menghasilkan kesetaraan:
D = 7.5m
Referensi
- Barnett, r. 2000. Pra-patung. 4. Edisi. Bukit McGraw.
- Larson, r. 2012. Pra-patung. Ke -8. Edisi. Pembelajaran Cengage.
- Pérez, v. Sifat kesetaraan aljabar. Pulih dari: matematika.LAGUIA2000.com.
- Sifat kesetaraan. Diperoleh dari: PPS.K12.Atau.kita.
- Stewart, J. 2007. Pra-kalkulasi: Matematika untuk perhitungan. Ke -5. Edisi. Pembelajaran Cengage.

