Hukum Tanda

Kami menjelaskan hukum tanda, dengan contoh dan latihan diselesaikan

Skema Hukum Tanda

Apa hukum tanda?

Itu Hukum Tanda Ini adalah serangkaian aturan yang digunakan dalam perhitungan aritmatika dan aljabar dengan bilangan real untuk menetapkan tanda dengan benar ke hasilnya, ketika jumlah positif dan negatif terlibat.

Ada aturan yang memadai sesuai dengan operasi yang dilakukan: jumlah, pengurangan, perkalian dan pembagian, yang merupakan yang paling mendasar, dan ada juga aturan tanda yang terkait dengan potensiasi dan operasi pengarsipan.

Dalam operasi yang diberikan, baik dengan tangan atau dengan kalkulator, perlu untuk menerapkan hukum tanda dengan benar untuk memastikan hasil yang benar, karena hanya perubahan kecil dalam tanda -tanda secara signifikan mengubah jumlahnya.

Hukum tanda -tanda untuk setiap operasi aritmatika dasar dan kasus -kasus yang mungkin timbul diperiksa di bawah ini.

Hukum tanda -tanda dalam jumlah

1) Jika angka yang akan ditambahkan memiliki tanda yang sama

Angka ditambahkan seperti biasa dan hasilnya ditambahkan ke tanda angka, terlepas dari apakah ini positif atau negatif.

Penting untuk diingat bahwa angka positif biasanya tidak ada sebelum tanda, tetapi ditulis secara langsung. Di sisi lain, angka negatif ditulis dalam tanda kurung, terutama ketika mereka didahului oleh simbol operasi aritmatika, untuk menghindari kebingungan.

Contoh jumlah angka dengan tanda yang sama:

3 + 9 = 12
4 + 7 + 1 + 6 = 18
(−3) + (−8) = −11
(−5) + (−10) + (−6) = −21

2) Jika angka yang akan ditambahkan memiliki tanda berbeda

Angka -angka dikurangi dan tanda angka yang memiliki nilai absolut terbesar ditambahkan ke hasilnya, baik positif atau negatif.

Sebagai contoh, lakukan operasi 5 + (−14). Karena nilai absolut (−14) lebih besar dari nilai absolut 5, 5 unit dikurangi dari 14, yang memberikan 9 dan hasil ini ditempatkan tanda negatif:

Dapat melayani Anda: prisma dan piramida

5 + (−14) = −9

Lebih banyak contoh aturan ini yang diterapkan pada jumlah dua jumlah tanda yang berbeda adalah:

(−27) + 12 = −15

12 + (−7) = 5

Jika dalam operasi ada lebih dari dua tambahan dengan tanda yang berbeda, Properti asosiatif dari jumlah:

(−20) + 9 + (−7) = [(−20) + 9] + (−7)

Operasi pertama kali dilakukan dalam pracete, yang terdiri dari jumlah dua jumlah tanda yang berbeda, yang aturan yang dijelaskan diterapkan: hasilnya dikurangi dan tanda angka dengan nilai absolut tertinggi:

(−20) + 9 = −11

Operasi seperti ini:

(−20) + 9 + (−7) = (−11) + (−7)

Sekarang Anda memiliki jumlah dua angka dari tanda yang sama, maka mereka biasanya ditambahkan dan hasilnya ditempatkan tanda negatif:

(−20) + 9 + (−7) = (−11) + (−7) = −18

Tanda -tanda di Pengganti

Pengurangan dua angka didefinisikan sebagai jumlah yang sebaliknya. Pada gilirannya, sebaliknya dengan angka dikatakan nomor dengan tanda yang diubah. Misalnya, kebalikan dari 2 adalah (−2), kebalikan dari (−5) adalah 5 dan seterusnya.

Dengan mengingat hal ini, ketika Anda memiliki pengurangan dua angka:

A - b

Itu hanya berubah menjadi jumlah kebalikan dari b:

A + ( - b)

Dan lanjutkan seperti yang dijelaskan di bagian sebelumnya. Catatan untuk menempatkan tanda + angka negatif tidak mengubahnya, tetapi sangat berhati -hati, yang sebaliknya tidak benar.

Ketika angka "A", yang merupakan minuend, lebih besar dari angka "B", yang dicuri, beroperasi seperti dalam pengurangan bilangan alami. Tidak masalah, karena sejumlah besar dikurangi dari jumlah yang lebih kecil:

Dapat melayani Anda: Ketimpangan segitiga: demonstrasi, contoh, latihan terpecahkan

25 - 8 = 17

Dengan contoh -contoh berikut, metode menambahkan sebaliknya untuk mengurangi sangat nyaman:

(−5) - 24 = (−5) +( - 24) = - 29
32 - (−23) = 32 + 23 = 55

Hukum tanda -tanda dalam perkalian

Hukum tanda -tanda dalam perkalian diterapkan dengan cara ini:

• Dengan mengalikan dua angka dari tanda yang sama, hasilnya selalu positif.
• Produk dari dua angka tanda yang berlawanan selalu negatif.

Ringkasan aturan tanda untuk perkalian ditunjukkan pada gambar:

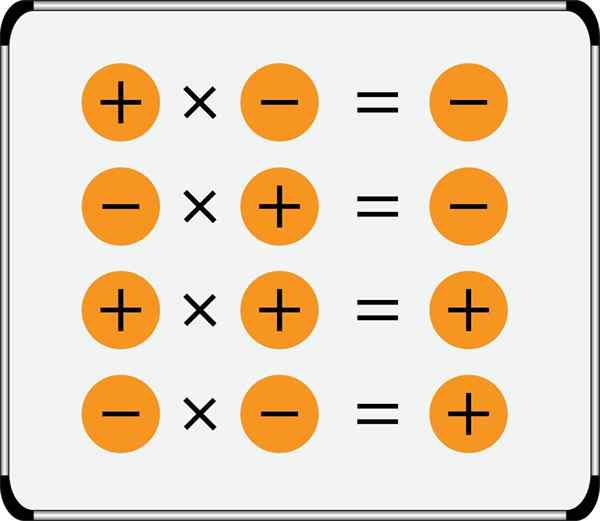
Perhatikan bahwa angka positif dapat ditulis tanpa tanda sebelumnya, tetapi angka negatif selalu memilikinya, di samping itu, dua simbol aritmatika tidak pernah ditulis satu sama lain, mereka harus selalu dipisahkan dengan tanda kurung, misalnya: misalnya:

Salah: 3 × −4
Benar: 3 × (−4) = −12

(−5) × 6 = −5 × 6 = −30
(−3) × (−11) = 33
10 × 27 = 270

Untuk melipatgandakan lebih dari dua angka, properti asosiatif dari perkalian digunakan, karena urutan faktor tidak mengubah produk, misalnya, saat melaksanakan:

(−2) × (−14) × 16

Anda dapat melipatgandakan dua faktor pertama, atau dua yang terakhir jika Anda mau, dan kemudian melipatgandakan hasilnya dengan faktor yang tersisa. Dalam hal ini, kedua faktor akan dikalikan terlebih dahulu dimulai di sebelah kiri:

[(−2) × (−14)] × 16

Produk dari dua angka negatif adalah positif, kemudian (−2) × (−14) = 28 dan tetap:

28 × 16 = 448

Hukum Tanda di Divisi

Ini analog dengan aturan tanda untuk perkalian:

• Rasio dua jumlah tanda yang sama selalu positif.
• Dengan membagi dua nomor tanda, hasilnya selalu negatif.

Itu dapat melayani Anda: perbedaan antara lingkaran dan keliling (dengan contoh)

Misalnya:

24 ÷ 8 = 3
−36 ÷ 3 = −12
162 ÷ (−9) = −18
−216 ÷ (−6) = 36

Hukum Tanda dalam Pemberdayaan dan Pengajuan

Eksponen nomor tertulis adalah:

ke^N

Di mana "a" adalah basis dan "n" adalah eksponen. Dua kasus dibedakan, menurut paritas eksponen:

Kasus 1: A positif

Ketika basisnya positif, hasilnya positif terlepas dari apakah eksponennya bahkan atau ganjil, seperti dalam:

2³ = 8
3⁴ = 81

Kasus 2: A negatif

Berikut dua kasus:

• Saat eksponen genap, maka hasilnya positif.
• Jika eksponen aneh, itu negatif.

Contoh

3² = 3 ∙ 3 = 9
2³ = 2 ∙ 2 ∙ 2 = 8
(−2)⁴ = (−2) ∙ (−2) ∙ (−2) ∙ (−2) = 16
(−3)³ = (−3) ∙ (−3) ∙ (−3) = −27

Operasi dengan simbol pengelompokan

Mereka sering muncul operasi terpisah dengan simbol pengelompokan: tanda kurung, kurung dan kunci. Ini dihilangkan dari dalam ke luar dengan mempertimbangkan hal -hal berikut:

• Jika simbol pengelompokan didahului dengan tanda positif, itu dapat dihapus tanpa mengubah tanda -tanda konten, misalnya: + (−3 + 5 - 1) = −3 + 5 - 1 = 1.
• Jika tanda negatif mendahului simbol grup, itu ditarik dengan menginvestasikan tanda konten, misalnya: - (−3 + 5 −1) = 3 - 5 + 1 = −1.
• Ketika ada operasi gabungan dari jumlah, pengurangan, perkalian dan pembagian, sifat asosiatif dan distributif dapat digunakan untuk kenyamanan.

Latihan terpecahkan

a) 10 + 10

Solusi: 20

b) (-8) + (-3)

Solusi: -11

c) (3) + (-10) 

Solusi: -7

D) (5) x (-3)

Solusi: -15

e) (-10) x (-10)

Solusi: 100

f) (18) ÷ (-3)

Solusi: -6

G) (-10) ÷ (-2)

Solusi: 5

h) 4 - ( - 7 + 9)

Solusi: 4 - ( - 7 + 9) = 4 + 7 - 9 = 11− 9 = 2