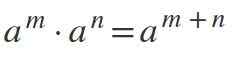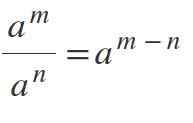Hukum eksponen

Apa hukum eksponen?

Itu Hukum eksponen Mereka adalah mereka yang berlaku untuk nomor itu yang menunjukkan berapa kali nomor dasar harus dikalikan dengan sendirinya. Eksponen juga dikenal sebagai Powers. Potensiasi adalah operasi matematika yang dibentuk oleh basis (a), eksponen (m) dan daya (b), yang merupakan hasil dari operasi.

Eksponen umumnya digunakan ketika jumlah yang sangat besar digunakan, karena ini tidak lebih dari singkatan yang mewakili penggandaan dari jumlah yang sama beberapa kali tertentu. Eksponen bisa positif dan negatif.

Apa eksponen dalam operasi matematika?

Seperti yang dinyatakan di atas, eksponen adalah bentuk singkat yang mewakili multiplikasi angka untuk diri mereka sendiri, di mana eksponen hanya terkait dengan angka kiri. Misalnya:

2³ = 2*2*2 = 8

Dalam hal ini nomor 2 adalah dasar daya, yang akan dikalikan 3 kali seperti yang ditunjukkan oleh eksponen, yang terletak di sudut kanan atas pangkalan. Ada berbagai cara membaca ekspresi: 2 meningkat menjadi 3 atau 2 yang diangkat ke kubus.

Eksponen juga menunjukkan berapa kali yang dapat dibagi, dan untuk membedakan operasi ini dari perkalian, eksponen membawa tanda minus (-) di depan dirinya sendiri (itu negatif), yang berarti bahwa eksponen berada dalam denominator dari sebagian kecil. Misalnya:

2^{- 4} = 1/2*2*2*2 = 1/16

Ini tidak boleh disamakan dengan kasus di mana basis negatif, karena akan tergantung pada apakah eksponen genap atau ganjil untuk menentukan apakah daya akan positif atau negatif. Dengan demikian Anda harus:

- Jika eksponennya rata, kekuatannya akan positif. Misalnya:

(-7)² = -7 _* -7 = 49.

- Jika eksponen aneh, daya akan negatif. Misalnya:

(-2)⁵ = (-2)*(-2)*(-2)*(-2)*(-2) = -32.

Ada kasus khusus di mana jika eksponen sama dengan 0, daya sama dengan 1. Ada juga kemungkinan bahwa pangkalannya adalah 0; Dalam hal ini, tergantung pada eksponen, daya akan tidak ditentukan atau tidak.

Untuk melakukan operasi matematika dengan eksponen, itu perlu.

Apa hukum eksponen?

Hukum Pertama: Kekuatan Eksponen sama dengan 1

Ketika eksponen adalah 1, hasilnya akan memiliki nilai yang sama dengan basis: a¹ = a.

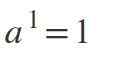
Contoh

9¹ = 9.

22¹ = 22.

895¹ = 895.

Hukum Kedua: Kekuatan Eksponen sama dengan 0

Ketika eksponen adalah 0, jika basis berbeda dari nol, hasilnya akan: a⁰ = 1.

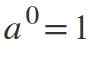
Contoh

1⁰ = 1.

323⁰= 1.

1095⁰ = 1.

Hukum Ketiga: Eksponen Negatif

Karena eksponen negatif, hasilnya akan menjadi fraksi, di mana daya akan menjadi penyebut. Misalnya, jika m positif, maka^-M = 1/a^M.

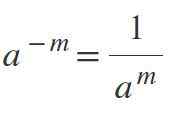
Contoh

- 3^-1 = 1/3.

- 6^-2 = 1/6² = 1/36.

- 8^-3 = 1/8³ = 1/512.

Undang -undang Keempat: Penggandaan kekuatan yang sama dengan hal yang sama

Untuk melipatgandakan kekuatan di mana pangkalannya sama dan berbeda dari 0, pangkalan dipertahankan dan eksponen ditambahkan: a^M _* ke^N = a^m+n.    

Contoh

- 4⁴ _* 4³ = 4⁴⁺³ = 4⁷

- 8¹ _* 8⁴ = 8¹⁺⁴ = 8⁵

- 2² _* 2⁹ = 2²⁺⁹ = 2^sebelas

Hukum Kelima: Divisi Tenaga dengan basis yang sama

Untuk membagi kekuatan di mana pangkalannya sama dan berbeda dari 0, pangkalan dipertahankan dan eksponen dikurangi sebagai berikut: a^M / ke^N = a^{M N}.    

Contoh

- 9² / 9¹ = 9 ^{(dua puluh satu)} = 9¹.

- 6^limabelas / 6¹⁰ = 6 ^{(15 - 10)} = 6⁵.

- 49¹² / 49⁶ = 49 ^{(12 - 6)} = 49⁶.

Undang -undang Keenam: Perkalian kekuatan yang berbeda dengan basis yang berbeda

Dalam undang -undang ini ada kebalikan dari apa yang diungkapkan di keempat; Yaitu, jika Anda memiliki basis yang berbeda tetapi dengan eksponen yang sama, pangkalan dikalikan dan eksponen dipertahankan: a^M _* B^M = (a_*B) ^M.

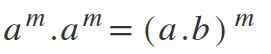
Contoh

- 10² _* dua puluh² = (10 _* dua puluh)² = 200².

- Empat. Lima^sebelas _* 9^sebelas = (45*9)^{11 =} 405^sebelas.

Cara lain untuk mewakili undang -undang ini adalah ketika penggandaan tinggi untuk kekuatan. Dengan demikian, eksponen akan menjadi milik masing -masing istilah: (a_*B)^M= a^M_* B^M.

Contoh

- (5_*8)⁴ = 5⁴ _* 8⁴ = 40⁴.

- (23 * 7)⁶ = 23⁶ _* 7⁶ = 161⁶.

Hukum Ketujuh: Divisi Tenaga yang Berbeda

Jika Anda memiliki basis yang berbeda tetapi dengan eksponen yang sama, basis dibagi dan eksponen dipertahankan:^M / B^M = (a / b)^M.

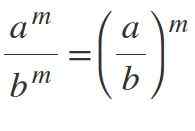
Contoh

- 30³ / 2³ = (30/2)³ = 15³.

- 440⁴ / 80⁴ = (440/80)⁴ = 5.5⁴.

Demikian pula, ketika suatu divisi tinggi ke kekuatan, eksponen akan termasuk dalam masing -masing istilah: (a / B) ^M = a^M /B^M.

Contoh

- (8/4)⁸ = 8⁸ / 4⁸ = 2⁸.

- (25/5)² = 25² / 5² = 5².

Ada kasus di mana eksponen negatif. Jadi, untuk menjadi positif, nilai pembilang diinvestasikan dengan nilai dari penyebut, sebagai berikut:

- (A / B)^-N = (b / a)^N = b^N / ke^N.

- (4/5) ^-9 = (5/4) ⁹ = 5⁹ / 4⁴.

Hukum Kedelapan: Kekuatan Kekuatan

Ketika Anda memiliki kekuatan yang dinaikkan ke kekuatan lain -yaitu, dua eksponen pada saat yang sama -pangkalan dipertahankan dan eksponen berlipat ganda: (a^M)^N= a^M*N.

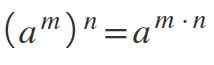
Contoh

- (8³)² = 8 ^(3*2) = 8⁶.

- (13⁹)³ = 13 ^(9*3) = 13²⁷.

- (238¹⁰)¹² = 238^{(10 * 12)} = 238¹²⁰.

Hukum Kesembilan: Eksponen Fraksional

Jika kekuatan memiliki sebagai eksponen fraksi, ini diselesaikan dengan mengubahnya menjadi akar N-esima, di mana pembilang tetap sebagai eksponen dan penyebut mewakili indeks root:

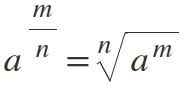
Contoh

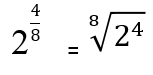
Latihan terpecahkan

Latihan 1

Hitung operasi antara kekuatan yang memiliki basis yang berbeda:

2⁴ _* 4⁴ / 8².

Larutan

Menerapkan aturan eksponen, pangkalan dikalikan dalam pembilang dan eksponen dipertahankan, seperti ini:

2⁴ _* 4⁴ / 8²= (2_*4)⁴ / 8²  = 8⁴ / 8²

Sekarang, karena ada basis yang sama, tetapi dengan eksponen yang berbeda, basis dipertahankan dan eksponen dikurangi:

 8⁴ / 8² = 8^{(4 - 2)} = 8²

Latihan 2

Hitung operasi antara kekuatan tinggi ke kekuatan lain:

(3²)³ _* (2 _* 6⁵)^-2 _* (2²)³

Larutan

Menerapkan hukum, Anda harus:

(3²)³ _* (2 _* 6⁵)^-2 _* (2²)³

= 3⁶ _* 2^-2 _* 2^-10 _* 2⁶

= 3⁶ _* 2^{(-2) + (- 10)} _* 2⁶

= 3⁶ _*  2^-12 _* 2⁶

= 3⁶ _* 2^{(-12) + (6)}

= 3⁶ _* 2⁶

= (3_*2)⁶

= 6⁶

= 46.656

Referensi

1. Aponte, g. (1998). Dasar -dasar Matematika Dasar. Pendidikan Pearson.
2. Corbalán, f. (1997). Matematika diterapkan pada kehidupan sehari -hari.
3. Jiménez, J. R. (2009). Matematika 1 Sep.
4. Max Peters, W. L. (1972). Aljabar dan Trigonometri.
5. Rees, hlm. K. (1986). Kembali.