Halaman rumah
Fisik
Momen formula inersia, persamaan dan contoh perhitungan

Fisik

Momen formula inersia, persamaan dan contoh perhitungan

4044
947
Pete Lesch

Dia momen inersia Dari tubuh yang kaku sehubungan dengan sumbu rotasi tertentu, ia mewakili ketahanannya untuk mengubah kecepatan sudut di sekitar sumbu itu. Ini sebanding dengan massa dan juga ke lokasi sumbu rotasi, karena tubuh, menurut geometri, dapat lebih mudah berputar di sekitar sumbu tertentu daripada di yang lain.

Misalkan objek yang luas (terdiri dari banyak partikel) yang dapat berputar di sekitar sumbu. Misalkan Kekuatan Kisah F, secara tangensial diterapkan pada elemen massa ΔM_yo, yang menghasilkan torsi atau momen, diberikan oleh τ_bersih= ∑R_yo X F_yo. Vektor R_yo Itu adalah posisi ΔM_yo(Lihat Gambar 2).

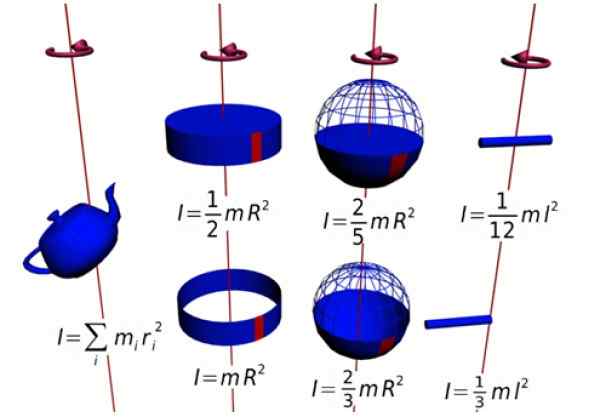
Gambar 1. Momen inersia dari beberapa figur. Sumber: Wikimedia Commons.

Momen ini tegak lurus terhadap bidang rotasi (alamat +K = meninggalkan kertas). Karena kekuatan dan posisi radial selalu tegak lurus, produk silang tetap:

τ_bersih = ∑ f_yo R_yo k = ∑ (ΔM_yoke_yo) R_yok = ∑ ΔM_yo(ke_yo R_yo) k

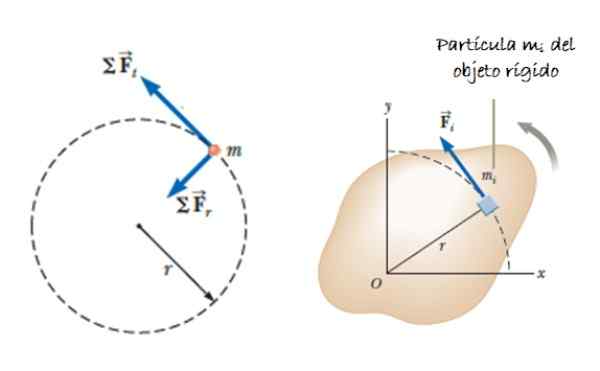Gambar 2. Sebuah partikel milik padatan yang kaku dalam rotasi. Sumber: Serway, R. 2018. Fisika untuk Sains dan Teknik. Volume 1. Pembelajaran Cengage.

Percepatan a_yo mewakili komponen tangensial percepatan, karena akselerasi radial tidak berkontribusi terhadap torsi. Tergantung pada akselerasi sudut α, kita dapat menunjukkan bahwa:

ke_yo = α r_yo

Oleh karena itu torsi bersih seperti ini:

τ_bersih = ∑ ΔM_yo(α r_yo²) K = (∑ R_yo² ΔM_yo) α k

Akselerasi sudut α adalah sama untuk seluruh objek, oleh karena itu tidak terpengaruh oleh subskrip "I" dan dapat meninggalkan jumlah, yang justru merupakan momen inersia dari objek yang dilambangkan dengan huruf I:

I = ∑ r_yo² ΔM_yo

Ini adalah momen inersia dari distribusi massa diskrit. Saat distribusi kontinu, jumlahnya diganti dengan integral dan ΔM menjadi diferensial massa DM. Integral dibuat di atas semua objek:

I = ∫_M(R²) Dm

Unit momen inersia dalam sistem internasional jika mereka kg x m². Itu adalah skalar dan jumlah positif, karena itu adalah produk adonan oleh kuadrat dari jarak.

[TOC]

Contoh perhitungan

Objek yang diperluas, seperti batang, cakram, bola atau lainnya, yang kepadatannya ρ Adalah konstan dan mengetahui bahwa kepadatan adalah hasil bagi massa, diferensial massa DM Itu ditulis sebagai:

ρ = dm/dv → dm = ρDv

Mengganti integral untuk momen inersia, kami memiliki:

I = ∫r² ρdv = ρ ∫r²Dv

Ini adalah ekspresi umum, valid untuk objek tiga dimensi, yang volumenya V dan posisi R Mereka adalah fungsi koordinat ruang X, Dan Dan z. Perhatikan bahwa menjadi konstan, kepadatannya tidak terpisahkan.

Kepadatannya ρ Ini juga dikenal sebagai kepadatan volumetrik, tetapi jika objeknya sangat datar, seperti lembaran atau sangat tipis dan sempit seperti batang, bentuk kepadatan lainnya dapat digunakan, mari kita lihat:

Dapat melayani Anda: gerakan rotasi bumi

- Untuk lembaran yang sangat halus, kepadatan yang akan digunakan adalah σ, kepadatan permukaan (massa per satuan area) dan memberi adalah diferensial area.

- Dan jika itu adalah batang tipis, di mana hanya panjangnya yang relevan, kepadatan massa linier digunakan λ dan diferensial panjang, sesuai dengan sumbu yang digunakan sebagai referensi.

Dalam contoh -contoh berikut, semua objek dianggap kaku (tidak dapat dideformasi) dan memiliki kepadatan yang seragam.

Momen inersia batang tipis sehubungan dengan sumbu yang melewati pusatnya

Di sini kita akan menghitung momen inersia batang yang tipis, kaku, homogen, dengan panjang L dan massa M, sehubungan dengan sumbu yang melewati cara.

Pertama -tama perlu untuk membangun sistem koordinat dan membangun angka dengan geometri yang memadai, seperti ini:

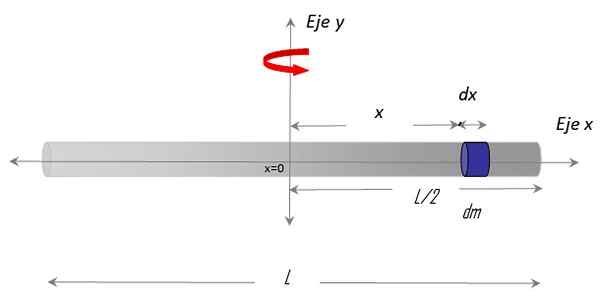Gambar 3. Geometri untuk menghitung momen inersia batang tipis sehubungan dengan sumbu vertikal yang melewati pusatnya. Sumber: f. Zapata.

Dia terpilih Sumbu x di sepanjang bar dan Sumbu y sebagai sumbu rotasi. Prosedur untuk membangun integral juga membutuhkan memilih diferensial massa di bar, yang disebut DM, yang memiliki panjang diferensial Dx dan terletak di posisi X sewenang -wenang, sehubungan dengan pusat x = 0.

Menurut definisi kepadatan massa linier λ:

λ = m/l

Ketika kepadatan seragam, yang berlaku untuk M dan L, itu juga untuk DM dan DX:

λ = dm/dx → dm = λdx.

Di sisi lain, elemen massa berada di posisinya X, Kemudian dengan mengganti geometri ini dalam definisi, kami memiliki integral yang pasti, yang batasnya adalah ekstrem dari batang sesuai dengan sistem koordinat:

$I=\int _Mr^2dm =\int_\frac-L2^\fracL2x^2\lambda dx=\lambda \left [\fracx^33 \right ]_\frac-L2^\fracL2=\frac\lambda 3\left [ \fracL^38-\left ( \frac-L^38 \right ) \right ]=\frac\lambda 12L^3$

Mengganti kepadatan linier λ = m/l:

$I=\frac112ML^2$

Untuk menemukan momen inersia batang sehubungan dengan sumbu rotasi lain, misalnya yang melewati salah satu ujungnya, Anda dapat menggunakan teorema Steiner (lihat latihan diselesaikan di akhir) atau melakukan perhitungan langsung yang mirip dengan itu ditampilkan di sini, tetapi memodifikasi geometri dengan benar.

Momen inersia album sehubungan dengan poros yang melewati pusatnya

Album yang sangat tipis, dengan ketebalan tercela adalah sosok yang datar. Jika adonan didistribusikan secara seragam di seluruh area A, kepadatan massa σ adalah:

σ = M/a

Banyak DM sebagai memberi sesuai dengan massa dan luas cincin diferensial yang ditunjukkan pada gambar. Kami akan berasumsi bahwa seluruh set berputar di sekitar sumbu dan.

Anda dapat membayangkan bahwa album ini disusun bahwa banyak cincin konsentris radio R, masing -masing dengan momen inersia masing -masing. Menambahkan kontribusi semua cincin sampai Anda mencapai radio R, Anda akan memiliki inersia total dari album.

σ = dm/da → dm = σmemberi

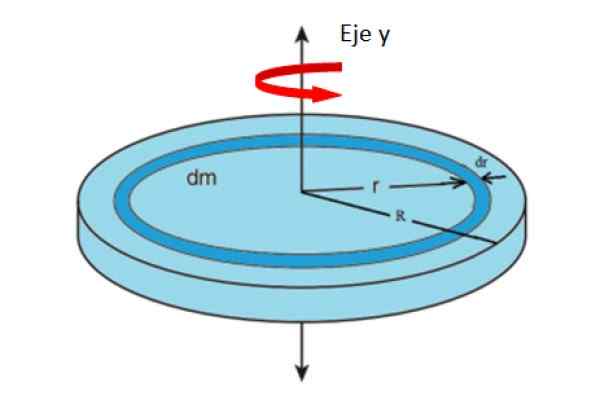Gambar 4. Geometri untuk menghitung momen inersia album, sehubungan dengan sumbu aksial. Sumber: f. Zapata.

Di mana m mewakili seluruh adonan album. Area album tergantung pada jari -jari R sebagai:

Dapat melayani Anda: kecepatan propagasi gelombang

A = π.R²

Berasal tentang r:

DA /DR = 2 = 2π.R → da = 2π.rdr

Mengganti yang di atas dalam definisi i:

$I=\int _Mr^2dm=\int_0^Rr^2\left (\sigma dA \right )=\sigma \int_0^Rr^2\left (2\pi rdr \right )=2\pi \sigma \int_0^Rr^3dr$ Setelah mengevaluasi hasil integral:

$I=2\pi \sigma \fracR^44$

Mengganti σ = m/(π.R²) tersisa:

$I=2\pi \sigma \fracR^44=2\pi\left (\fracM\pi R^2 \right )\left (\fracR^44 \right )=\frac12MR^2$

Momen inersia bola padat sehubungan dengan diameter

Radius R Sphere dapat dianggap sebagai serangkaian cakram bertumpuk di atas satu sama lain, di mana setiap album massa yang sangat kecil DM, radio R dan ketebalan Dz, Ini memiliki momen inersia yang diberikan oleh:

telah memberi_disk = (½) r²DM

Untuk menemukan diferensial ini, formula bagian sebelumnya hanya diambil dan diganti M Dan R oleh DM Dan R, masing -masing. Album seperti ini dapat dilihat di geometri Gambar 5.

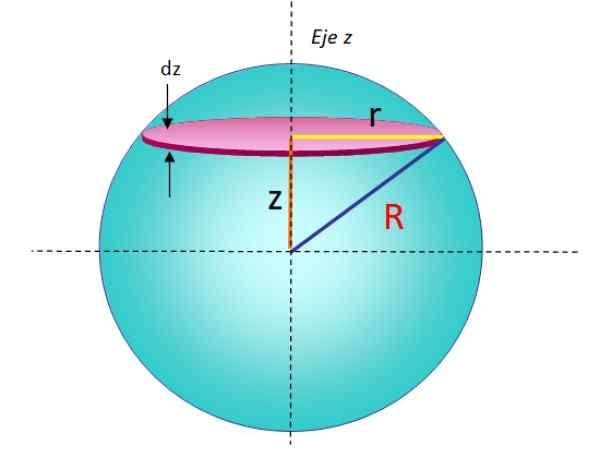Gambar 5. Geometri untuk menghitung momen inersia dari bola jari -jari padat sehubungan dengan sumbu yang melewati diameter. Sumber: f. Zapata.

Dengan menambahkan semua momen inersia infinitesimal dari cakram bertumpuk, momen inersia total dari bola diperoleh:

yo_bola = ∫di_disk

Yang setara dengan:

I = ∫_bola(½) r²DM

Untuk menyelesaikan integral, Anda perlu mengekspresikan DM dengan baik. Seperti biasa, itu dicapai dari kepadatan:

ρ = m/v = dm/dv → dm = ρ.Dv

Volume disk diferensial adalah:

DV = Area Basis X Tinggi

Ketinggian album adalah ketebalan Dz, Sedangkan area dasarnya πr², Karena itu:

Dv = πr²Dz

Dan mengganti yang terintegrasi akan seperti ini:

I = ∫_bola(½) r²Dm = ∫ (½) r²(ρπr²DZ)

Tapi sebelum berintegrasi, itu harus. Melalui Teorema Pythagoras:

R² = r² + z² → R² = R² - z²

Itu menuntun kita ke:

I = ∫_bola(½) ρ r²(πr²dz) = ∫_bola(½) ρ π r⁴Dz= ∫_bola(½) ρ π (r² - z²)² Dz

Untuk mengintegrasikan seluruh bidang, kami melihat bahwa Z bervariasi antara -r dan r, oleh karena itu:

$I=\frac12\pi \rho \left [\int_-R^RR^4dz-\int_-R^R2R^2z^2dz+\int_-R^Rz^4dz \right ]$
$I=\frac12\pi \rho \left [R^4z-2R^2\left (\fracz^33 \right )+\fracz^55 \right ]_-R^R=\frac815\pi \rho R^^5$

Mengetahui bahwa ρ = m/v = m/[(4/3) πr³] Akhirnya, diperoleh, setelah menyederhanakan:

$I=\frac815\pi \left (\fracM\frac43\pi R^3 \right )R^5=\frac25MR^2$

Momen inersia silinder padat sehubungan dengan sumbu aksial

Untuk objek ini metode yang mirip dengan yang digunakan untuk bola digunakan, hanya saja kali ini lebih mudah jika silinder dibayangkan untuk cangkang silinder radio R, ketebalan Kata dan tinggi H, Seolah -olah mereka adalah lapisan bawang.

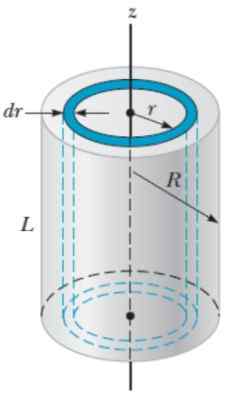Gambar 6. Geometri untuk menghitung momen inersia dari silinder jari -jari padat R Menghormati sumbu aksial. Sumber: Serway, R. 2018. Fisika untuk Sains dan Teknik. Volume 1. Cengage.

Volume Dv dari lapisan silinder adalah:

Dv = 2π.Rl.Kata

Oleh karena itu massa cascaron adalah:

Dapat melayani Anda: Skala Mikroskopis: Properti, Partikel Hitung, Contoh

Dm = ρ.Dv = ρ. 2π.R.L.Kata

Ekspresi ini diganti dalam definisi momen inersia:

$I=\int _Mr^2dm = \int_0^Rr^22\pi \rho Lrdr=2\pi \rho L\int_0^Rr^3dr=2\pi \rho L\left (\fracR^44 \right )$ Mengingat bahwa ρ = m / (π.R²L) tersisa:

$I=2\pi \left (\fracM\pi R^2L \right ) L\left (\fracR^44 \right )=\frac12MR^2$

Persamaan sebelumnya menunjukkan bahwa momen inersia silinder tidak tergantung pada panjangnya, tetapi pada massa dan radius saja saja. Ya L berubah, momen inersia sehubungan dengan sumbu aksial akan terus sama. Untuk alasan ini, yo dari silinder bertepatan dengan album tipis yang sebelumnya dihitung sebelumnya.

Momen inersia lembaran persegi panjang sehubungan dengan sumbu yang melewati pusatnya

Itu Sumbu y Horizontal sebagai sumbu rotasi. Gambar di bawah ini menunjukkan geometri yang diperlukan untuk melakukan integrasi:

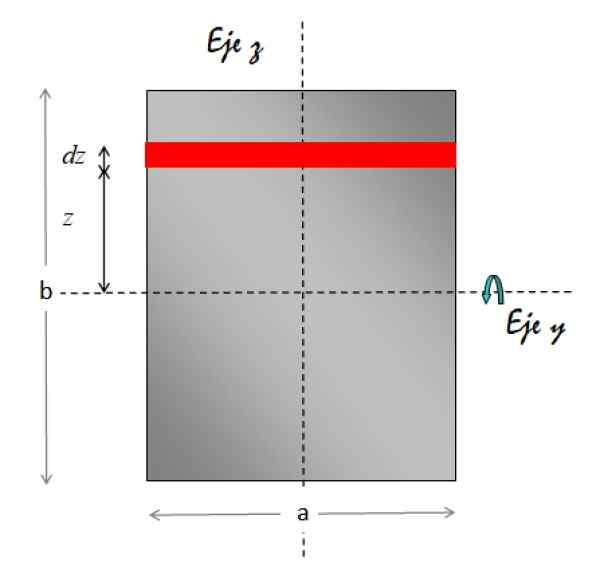Gambar 7. Geometri untuk perhitungan momen inersia pelat persegi panjang sehubungan dengan sumbu paralel ke lembaran dan yang melewati pusatnya. Sumber: f. Zapata.

Elemen area yang ditunjukkan dengan warna merah adalah persegi panjang. Areanya adalah basis x tinggi, oleh karena itu:

da = a.Dz

Oleh karena itu diferensial massa adalah:

Dm = σ.da = σ.(ke.DZ)

Adapun jarak elemen area ke sumbu rotasi, selalu z. Kami mengganti semua ini di integral momen inersia:

$I=\int _Mz^2dm=\int_\frac-b2^\fracb2z^2\left (\sigma adz \right )=\sigma a\int_\frac-b2^\fracb2z^2dz=\sigma a\left [ \fracz^33 \right ]_\frac-b2^\fracb2=\frac112\sigma ab^3$

Sekarang kepadatan massa permukaan σ digantikan oleh:

σ = m/ab

Dan pasti seperti ini:

$I=\frac112\sigma ab^3=\frac112\left ( \fracMab \right )ab^3=\frac112Mb^2$

Perhatikan bahwa itu seperti bilah tipis.

Momen inersia lembaran persegi sehubungan dengan sumbu yang melewati pusatnya

Untuk persegi di samping L, Dalam ekspresi sebelumnya valid untuk persegi panjang, nilai B oleh satu L:

$I=\frac112ML^2$

Teorema momen inersia

Ada dua teorema yang sangat berguna untuk menyederhanakan perhitungan momen inersia sehubungan dengan sumbu lain, yang sebaliknya bisa rumit untuk menemukan kurangnya simetri. Teorema ini adalah:

Teorema Steiner

Disebut juga Teorema Sumbu Paralel, menghubungkan momen inersia mengenai sumbu dengan orang lain yang melewati pusat massa objek, selama sumbu paralel. Untuk menerapkannya, jarak D perlu diketahui antara dua sumbu dan tentu saja massa m dari objek.

Menjadi yo_zMomen inersia dari objek yang diperluas sehubungan dengan Z, saya poros_CmMomen inersia sehubungan dengan sumbu yang melewati pusat massa (cm) objek tersebut, maka dipenuhi bahwa:

yo_z = I_Cm + Md²

Atau dalam notasi gambar berikut: yo_{z '} = I_z + Md²

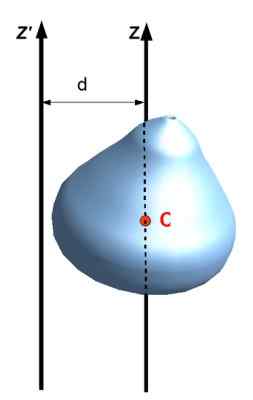Angka 8. Teorema Steiner atau sumbu paralel. Sumber: Wikimedia Commons. Jack Lihat [CC BY-SA (https: // CreationCommons.Org/lisensi/by-sa/3.0)]

Teorema sumbu tegak lurus

Teorema ini berlaku untuk permukaan datar dan mengatakan: Momen inersia dari benda datar di sekitar sumbu tegak lurus terhadapnya adalah jumlah momen inersia di sekitar dua sumbu tegak lurus terhadap sumbu pertama:

yo_z = I_X + yo_Dan

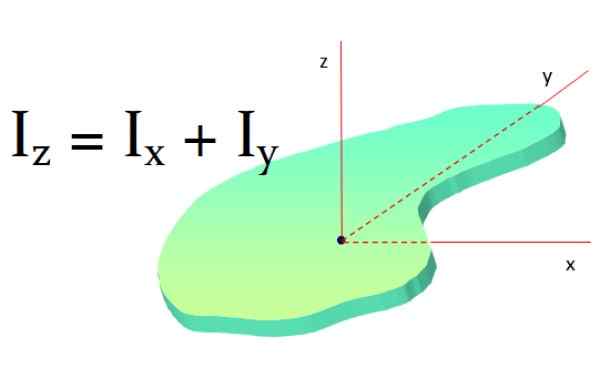Gambar 9. Teorema sumbu tegak lurus. Sumber: f. Zapata.

Jika objek memiliki simetri seperti itu yo_X Dan yo_Dan Mereka sama, maka terpenuhi bahwa:

yo_z = 2i_X

Olahraga diselesaikan

Temukan momen inersia batang sehubungan dengan sumbu yang melewati salah satu ujungnya, seperti yang ditunjukkan pada Gambar 1 (di bawah dan ke kanan) dan Gambar 10.

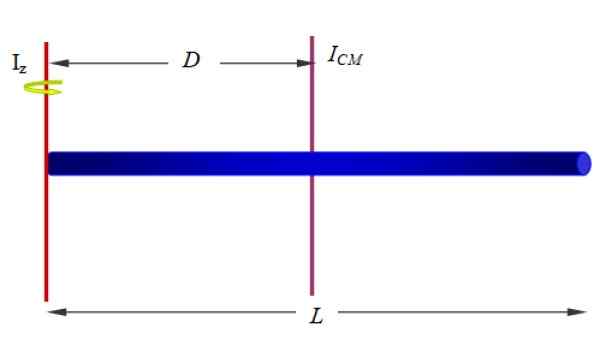Gambar 10. Momen inersia bar homogen di sekitar sumbu yang melewati satu ujung. Sumber: f. Zapata.

Larutan:

Kami sudah memiliki momen inersia bar di sekitar sumbu yang melewati pusat geometrisnya. Karena bilahnya homogen, pusat massa pada saat itu, jadi ini akan menjadi milik kita yo_Cm Untuk menerapkan teorema Steiner.

Jika panjang bilah L, Sumbu z berada pada jarak d = l/2, oleh karena itu: oleh karena itu:

yo_z = I_Cm + Md²= (1/12) ml²+M (l/2)²= (1/3) ml²

Referensi

Bauer, w. 2011. Fisika untuk Teknik dan Ilmu Pengetahuan. Volume 1. MC Graw Hill. 313-340
Rex, a. 2011. Dasar -dasar fisika. Pearson. 190-200.
Teorema Sumbu Paralel. Pulih dari: hyperphysics.Phy-astr.GSU.Edu.
Serway, r. 2018. Fisika untuk Sains dan Teknik. Volume 1. Cengage.
Universitas Sevilla. Momen inersia padatan bola. Pulih dari: Laplace.kita.adalah.
Universitas Sevilla. Momen inersia sistem partikel. Pulih dari: Laplace.kita.adalah.
Wikipedia. Teorema Sumbu Paralel. Diperoleh dari: di.Wikipedia.org