Gerakan Pendular

Apa itu gerakan pendular?

Dia Gerakan Pendular Ini adalah gerakan ayun yang dibuat oleh benda yang kurang lebih berat, yang disebut pendulum, ditangguhkan oleh tali atau batang cahaya, dipasang di ujung lainnya.

Pendulum diberikan impuls awal dan diizinkan untuk berosilasi, dengan cara ini objek menggambarkan lengkungan pulang pergi. Ini adalah prinsip pengoperasian jam tangan pendulum, ayunan, kursi goyang dan Metronom pendulum, digunakan untuk menandai waktu dalam musik.

Pendulum berosilasi, menunjukkan kecepatan dan akselerasi (Wikipedia.org)

Dikatakan bahwa pada 1581, Galileo Galilei mengamati pengaruh lampu di katedral Pisa, mengamati bahwa, meskipun amplitudo osilasi kandil berkurang karena gesekan dengan udara, bukan durasi durasi durasi durasi durasi tersebut durasi durasi tersebut dari durasi siklus.

Ini menarik perhatian Galileo, yang memutuskan untuk melanjutkan penelitian dan menentukan bahwa periode pendulum tidak tergantung pada adonan, tetapi pada akar kuadrat panjang tali, seperti yang akan terlihat nanti.

Karakteristik gerakan pendular

Pendulum sangat mudah dibangun, karena cukup dengan segi gantung benang kapas dan memegang di ujung lain dengan jari -jari Anda atau dengan mengikatnya ke dukungan seperti paku.

Setelah impuls awal yang kecil, beratnya bertanggung jawab untuk menjaga pendulum tetap berosilasi, meskipun gesekannya mengurangi amplitudo gerakan, sampai akhirnya berhenti berhenti.

Fitur utama dari gerakan pendular adalah untuk berulang, karena itu adalah gerakan goyangan. Sekarang, untuk memfasilitasi studi Anda, lebih mudah untuk membuat beberapa penyederhanaan untuk fokus pada model yang lebih sederhana, yang disebut pendulum sederhana.

Pendulum sederhana

Anak dalam ayunan dapat dimodelkan sebagai pendulum sederhana

Ini adalah sistem yang ideal yang terdiri dari tegak lurus, dianggap sebagai massa tepat waktu M, tunduk pada tali panjang dan tidak mudah dibujuk L. Karakteristik sistem ini adalah:

• Memiliki gerakan berulang dan periodik, yang terdiri dari bolak -balik lingkar radius yang sama dengan l.
• Tidak memperhitungkan gesekan.
• Amplitudo gerakan itu kecil (< 5º).
• Periode tersebut tidak tergantung pada massa M, Dan itu hanya tergantung panjangnya L dari pendulum.

Dapat melayani Anda: vektor yang dihasilkan: perhitungan, contoh, latihan

Rumus dan Persamaan

Berikut ini adalah diagram pendulum sederhana, di mana dua kekuatan bertindak: berat P magnitude mg, yang diarahkan secara vertikal ke bawah dan ketegangan T Di tali. Mereka tidak dianggap gesekan.

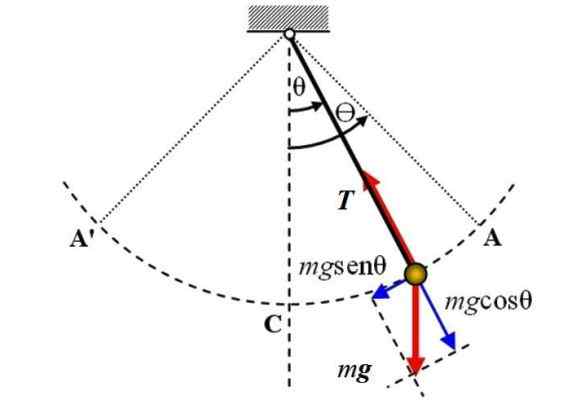Diagram tubuh bebas dari pendulum sederhana. Sumber: Wikimedia Commons.

Sumbu referensi adalah sumbu vertikal dan bertepatan dengan posisi θ = 0, dari sana perpindahan sudut θ diukur, baik dalam satu arah atau lainnya. Tanda + dapat ditugaskan ke kanan dalam gambar.

Untuk mempelajari gerakan pendulum, sistem koordinat dipilih dengan asal di pendulum itu sendiri. Sistem ini memiliki koordinat tangensial dengan busur lingkar A'CA yang dijelaskan oleh pendulum, serta koordinat radial, diarahkan ke pusat lintasan.

Pada saat yang ditunjukkan pada gambar, pendulum bergerak ke kanan, tetapi komponen tangensial gravitasi, yang disebut f_T, bertanggung jawab untuk membuatnya kembali. Perlu diperingatkan bahwa komponen ini masuk akal bertentangan dengan gerakan.

Adapun tegangan pada tali, itu seimbang dengan komponen berat mgcosθ.

Gaya jaring, kemudian, yang disebut f_T Dan oleh hukum kedua Newton sama dengan produk Akselerasi massa ×, Dan ini pada gilirannya adalah yang kedua berasal dari perpindahan linier S, Apa busur yang dilalui oleh pendulum. Jadi:

Perpindahan sudut 

Persamaan harus diekspresikan dalam hal variabel tunggal, mengingat bahwa perpindahan sudut θ dan lengkungan yang ditempuh terkait dengan persamaan:

Ini dapat melayani Anda: Hukum Kedua Termodinamika: Rumus, Persamaan, Contoh

s = l.θ

Massa dibatalkan di kedua sisi dan jika amplitudo kecil, sudut θ juga, dengan cara pendekatan berikut ini valid:

sin θ ≈ θ

Dengan ini, persamaan diferensial berikut untuk variabel θ (t) diperoleh:

Persamaan ini sangat mudah dipecahkan, karena solusinya adalah fungsi yang turunan keduanya adalah fungsi itu sendiri. Ada tiga alternatif: cosinus, satu payudara atau eksponensial. Fungsi cosinus dipilih untuk perpindahan sudut θ (t), karena merupakan fungsi yang diketahui dan mudah ditangani dengan baik.

Pembaca dapat memeriksa, memperoleh dua kali, bahwa fungsi berikut memenuhi persamaan diferensial:

θ (t) = θ_M cos (ωt + φ)

Dimana θ_M Ini adalah sudut maksimum bahwa pendulum bergerak sehubungan dengan frekuensi vertikal dan sudut Ω adalah:

Φ konstan ditambahkan untuk memberikan umum pada solusi dan cocok sesuai dengan kondisi awal.

Persamaan periode

Periode T gerakan adalah waktu yang diperlukan untuk melakukan siklus dan didefinisikan sebagai:

Mengganti Ω:

Seperti yang ditetapkan sebelumnya, periode tidak tergantung pada massa pendulum, tetapi hanya pada panjangnya.

Contoh gerakan pendular

Ukuran detak jantung

Galileo memiliki terjadinya mengukur detak jantung orang, menyesuaikan panjang pendulum sampai periode dengan denyut jantung seseorang bertepatan.

Jam pendulum

Ini tidak diragukan lagi salah satu contoh gerakan pendular yang paling akrab. Pembuatan jam tangan pendulum memiliki sains dan seni. Fisikawan Belanda Christian Huygens (1629-1695) mengembangkan arloji pendulum pertama pada tahun 1656, berdasarkan penelitian yang dibuat bertahun-tahun yang lalu oleh Galileo.

Dapat melayani Anda: optik bergelombang

Pendulum Foucault

Pendulum foucault. Sumber: Wikimedia Commons.

Ini adalah pendulum yang agak berbeda dari yang dijelaskan di atas, karena mampu berputar di bidang vertikal apa pun. Itu dibuat oleh fisikawan Prancis Léon Foucault (1819-1868) dan digunakan untuk memvisualisasikan rotasi bumi.

Olahraga diselesaikan

Pendulum sederhana melewati setiap 0.5 detik untuk posisi ekuilibrium. Berapa panjang utas?

Larutan

Karena periode adalah waktu yang diperlukan untuk membuat siklus lengkap, di mana ia melewati dua kali melalui posisi kesetimbangan: satu pertama dan yang lainnya kembali, lalu: lalu:

T = 2 × 0.5 s = 1 detik

Dari:

Panjang l utas dibersihkan:

Utas berukuran 0.Panjang 25 m atau 25 cm.

Referensi

1. Figueroa, d. (2005). Seri: Fisika untuk Sains dan Teknik. Volume 2. Dinamis. Diedit oleh Douglas Figueroa (USB).
2. Giambattista, a. 2010. Fisika. 2nd. Ed. Bukit McGraw.
3. Giancoli, d.  2006. Fisika: Prinsip dengan aplikasi. 6. Ed Prentice Hall.
4. Katz, d. 2013. Fisika untuk Ilmuwan dan Insinyur. Yayasan dan Koneksi. Pembelajaran Cengage.
5. Knight, r.  2017. Fisika untuk Ilmuwan dan Teknik: Pendekatan Strategi.  Pearson.