Karakteristik, jenis, dan contoh gerakan bujursangkar

Dia Gerakan bujursangkar Ini adalah salah satu di mana ponsel bergerak di sepanjang garis lurus dan karenanya melewati dimensi, karenanya juga menerima nama Gerakan unidimensional. Garis lurus ini adalah lintasan atau jalur diikuti oleh objek yang bergerak. Mobil -mobil yang bepergian di sepanjang jalan Gambar 1 Ikuti jenis gerakan ini.

Ini adalah model gerakan paling sederhana yang dapat dibayangkan. Pergerakan harian manusia, hewan, dan hal -hal sering menggabungkan transfer dalam garis lurus dengan gerakan di sepanjang kurva, tetapi beberapa sering mengamati beberapa yang secara eksklusif bubur secara eksklusif.

Gambar 1. Mobil bergerak di sepanjang jalan bujursangkar. Sumber: Pixabay.

Berikut beberapa contoh yang bagus:

- Saat berlari sepanjang trek bujursangkar 200 meter.

- Mengemudi mobil di jalan lurus.

- Menjatuhkan objek dengan bebas dari ketinggian tertentu.

- Saat bola dilemparkan secara vertikal.

https: // giphy.com/gifs/j5xx3bynaqv06wtoxq

Sekarang, tujuan menggambarkan suatu gerakan dicapai dengan menentukan karakteristik seperti:

- Posisi

- Pemindahan

- Kecepatan

- Percepatan

- Waktu.

Agar pengamat mendeteksi pergerakan suatu objek, perlu memiliki titik referensi (asal o) dan telah menetapkan alamat spesifik untuk bergerak, yang dapat menjadi sumbu X, sumbu Dan atau lainnya.

Adapun objek yang bergerak, ini dapat memiliki banyak cara. Tidak ada batasan dalam hal ini, namun dalam segala hal yang mengikuti akan diasumsikan bahwa ponsel adalah sebuah partikel; objek yang begitu kecil sehingga dimensinya tidak relevan.

Diketahui bahwa ini bukan kasus untuk objek makroskopis; Namun, ini adalah model dengan hasil yang baik dalam deskripsi pergerakan global suatu objek. Dengan cara ini, sebuah partikel bisa berupa mobil, planet, seseorang atau objek lain yang bergerak.

Kami akan memulai studi kami tentang kinematika bujursangkar dengan pendekatan umum untuk gerakan dan kemudian kasus -kasus tertentu akan dipelajari sebagai yang sudah ditunjuk.

[TOC]

Karakteristik umum gerakan bujursangkar

Deskripsi berikut ini umum dan berlaku untuk semua jenis gerakan satu -dimensi. Hal pertama adalah memilih sistem referensi. Garis di mana gerakan terjadi akan menjadi poros X. Parameter gerakan:

Posisi

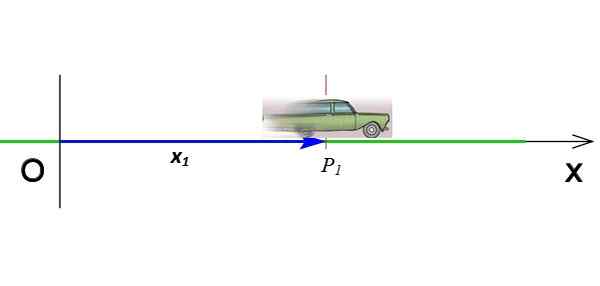Gambar 2. Posisi ponsel yang bergerak pada sumbu x. Sumber: Wikimedia Commons (dimodifikasi oleh f. Zapata).

Itu adalah vektor yang beralih dari asal ke titik di mana objek dalam sekejap diberikan. Pada Gambar 2, vektor X₁ Menunjukkan posisi ponsel saat berada dalam koordinat P₁ dan pada waktunya T₁. Unit vektor posisi dalam sistem internasional adalah meter.

Pemindahan

Perpindahan adalah vektor yang menunjukkan perubahan posisi. Pada Gambar 3 mobil telah berubah dari posisi P₁ ke posisi itu P₂, Oleh karena itu perpindahannya adalah ΔX = X₂ - X₁. Perpindahan adalah pengurangan dua vektor, dilambangkan dengan huruf Yunani Δ ("delta") dan pada gilirannya vektor. Unit -unitnya dalam sistem internasional adalah meter.

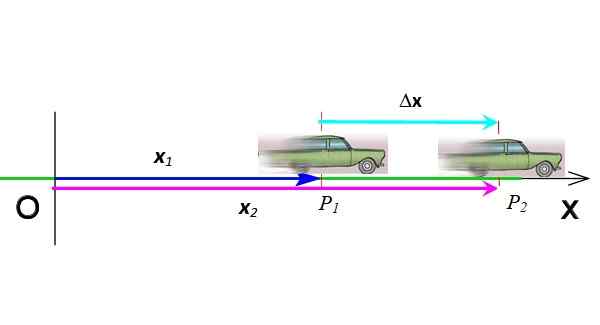Gambar 3. Perpindahan vektor. Sumber: disiapkan oleh f. Zapata.

Vektor dilambangkan dengan huruf tebal dalam teks cetak. Tetapi berada pada dimensi yang sama, jika diinginkan Anda dapat melakukannya tanpa notasi vektor.

Dapat melayani Anda: cabang fisika klasik dan modern

Jarak ditempuh

Jarak D Tur oleh objek bergerak adalah nilai absolut dari vektor perpindahan:

D = ΙXΙ = δX

Menjadi nilai absolut, jarak yang ditempuh selalu lebih besar dari atau sama dengan 0 dan unitnya sama dengan posisi posisi dan perpindahan. Notasi nilai absolut dapat dilakukan dengan bilah modul atau hanya menghapus huruf tebal dalam teks yang dicetak.

Kecepatan rata-rata

Seberapa cepat posisi berubah? Ada ponsel yang lambat dan cepat. Kuncinya selalu menjadi kecepatan. Untuk menganalisis faktor ini, posisi dianalisis X fungsi waktu T.

Kecepatan rata -rata v_M (Lihat Gambar 4) Ini adalah kemiringan garis pengeringan (fuchsia) ke kurva X Vs T dan memberikan informasi global tentang perpindahan seluler dalam interval waktu yang dipertimbangkan.

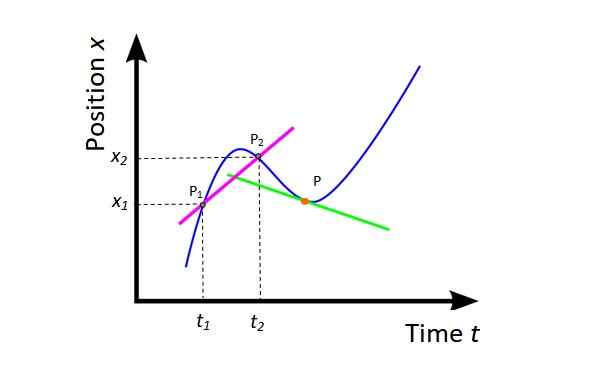Gambar 4. Kecepatan rata -rata dan kecepatan instan. Sumber: Wikimedia Commons, dimodifikasi oleh f. Zapata.

v_M = (X₂ - X₁) / (T₂ -T₁) = ΔX / ΔT

Kecepatan rata -rata adalah vektor yang unitnya dalam sistem internasional adalah meter /detik (MS).

Kecepatan seketika

Kecepatan rata -rata dihitung dengan mengambil interval waktu yang terukur, tetapi tidak menginformasikan tentang apa yang terjadi dalam interval tersebut. Untuk mengetahui kecepatan kapan saja, Anda harus membuat interval waktu menjadi sangat kecil, secara matematis sama dengan melakukan:

Δt → 0

Persamaan sebelumnya diberikan untuk kecepatan rata -rata. Dengan cara ini kecepatan instan atau kecepatan hanya diperoleh:

Secara geometris, turunan dari posisi sehubungan dengan waktu adalah kemiringan garis yang bersinggungan dengan kurva X Vs T pada titik tertentu. Pada Gambar 4 titiknya oranye dan garis singgung berwarna hijau. Kecepatan sesaat pada titik ini adalah kemiringan garis itu.

Kecepatan

Kecepatan didefinisikan sebagai modul nilai absolut atau kecepatan dan selalu positif (pensinyalan, jalan dan jalan raya selalu positif, tidak pernah negatif). Istilah "kecepatan" dan "kecepatan" dapat digunakan setiap hari, tetapi dalam fisika perbedaan antara vektor dan pendakian diperlukan.

v = ΙvΙ = v

Akselerasi rata -rata dan percepatan instan

Kecepatan dapat berubah dalam perjalanan gerakan dan kenyataannya adalah diharapkan untuk melakukannya. Ada besarnya yang mengukur perubahan ini: akselerasi. Jika kita melihat bahwa kecepatan adalah perubahan posisi sehubungan dengan waktu, akselerasi adalah perubahan kecepatan sehubungan dengan waktu.

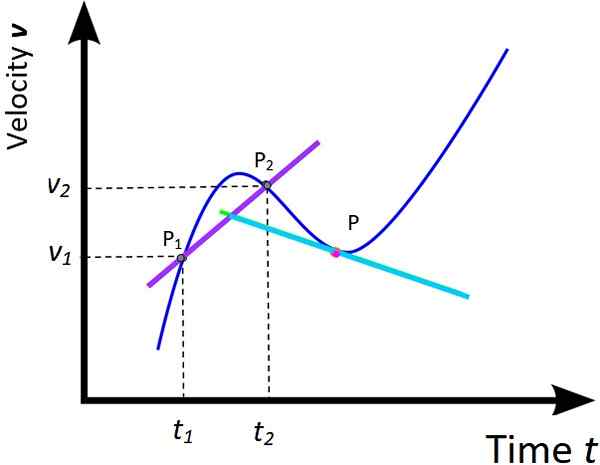Gambar 5. Akselerasi rata -rata dan percepatan instan. Sumber: Wikimedia Commons, dimodifikasi oleh f. Zapata.

Perawatan yang diberikan pada grafik X Vs T Dari dua bagian sebelumnya dapat diperluas ke grafik yang sesuai v Vs T. Akibatnya, percepatan rata -rata dan percepatan instan didefinisikan sebagai:

ke_M = (v₂ - v₁) / (T₂ -T₁) = Δv / ΔT  (Menunggu tempat tinggal)

Percepatan dan perlambatan

Dalam gerakan satu dimensi, vektor berdasarkan konvensi memiliki tanda -tanda positif atau negatif saat mereka berjalan dengan satu atau lain cara. Ketika akselerasi memiliki arti yang sama dengan kecepatan, ia meningkatkan besarnya, tetapi ketika itu masuk akal dan kecepatannya berkurang besarnya. Kemudian dikatakan bahwa gerakan itu tertunda.

Dapat melayani Anda: Leyden Bottle: Bagian, Operasi, Eksperimen

Teman-teman

Klasifikasi gerakan rektilin biasanya dilakukan berdasarkan:

- Apakah akselerasinya konstan atau tidak.

- Gerakan ini melewati garis horizontal atau vertikal.

Gerakan dengan akselerasi konstan

https: // giphy.com/gifs/ylzfnbidhm7rp391fi

Saat akselerasi konstan, percepatan rata -rata ke_M Itu sama dengan akselerasi instan ke Dan ada dua opsi:

- Bahwa akselerasinya bernilai 0, dalam hal ini kecepatan konstan dan memiliki gerakan bujursangkar yang seragam atau MRU.

- Akselerasi konstan berbeda dari 0, di mana kecepatan tumbuh atau berkurang secara linear dari waktu ke waktu (gerakan bujursangkar secara seragam bervariasi atau mruv):

Di mana v_F  Dan T_F Mereka masing -masing adalah kecepatan dan waktu terakhir, dan v_{salah satu} Dan T_{salah satu} Mereka adalah kecepatan dan waktu awal. Ya T_{salah satu} = 0, Saat membersihkan kecepatan akhir, Anda memiliki persamaan yang sudah akrab untuk kecepatan akhir:

v_F = v_{salah satu} + PADA

Untuk gerakan ini, persamaan berikut juga valid:

- Posisi tergantung waktu: x = x_{salah satu} + v_{salah satu .}t +½ at²

- Kecepatan tergantung pada posisinya: v_F² = v_{salah satu}² + 2nd.ΔX  (Dengan δx = x - x_{salah satu})

Gerakan horizontal dan gerakan vertikal

Gerakan horizontal adalah gerakan yang melewati sumbu horizontal atau sumbu x, sedangkan yang vertikal melakukannya di sepanjang sumbu dan sumbu. Gerakan vertikal di bawah aksi gravitasi adalah yang paling sering dan menarik.

Dalam persamaan sebelumnya, ini diambil A = g = 9.8 m/s² diarahkan ke bawah secara vertikal, arah yang hampir selalu dipilih dengan tanda negatif.

Cara ini, v_F = v_{salah satu} + PADA Itu berubah v_F = v_{salah satu} - GT Dan jika kecepatan awal adalah 0 karena objek dijatuhkan secara bebas, semakin disederhanakan v_F = - gt. Selama resistensi udara tidak diperhitungkan, tentu saja.

Contoh terpecahkan

Contoh 1

Pada titik, paket kecil dilepaskan sehingga bergerak di sepanjang transporter dengan roda geser ABCD yang ditunjukkan pada gambar. Saat turun melalui bagian miring AB dan CD, paket membawa akselerasi 4,8 m/s², Sedangkan di bagian horizontal BC mempertahankan kecepatan konstan.

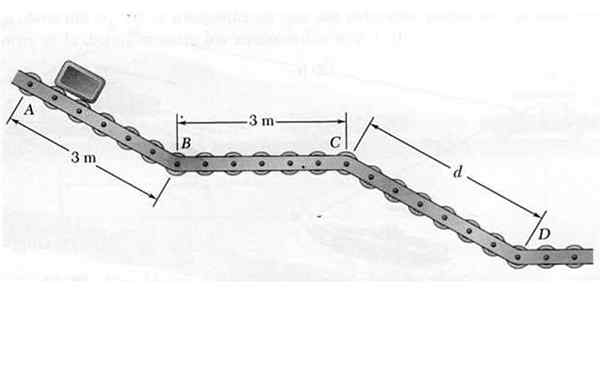Gambar 6. Paket yang bergerak di jalur geser dari contoh yang diselesaikan 1. Sumber: Made sendiri.

Mengetahui bahwa kecepatan paket di D tercapai adalah 7,2 m/s, tentukan:

a) Jarak antara C dan D.

b) waktu yang diperlukan untuk paket untuk mencapai akhir.

Larutan

Pergerakan paket dilakukan di tiga bagian bujursangkar yang ditunjukkan dan untuk menghitung yang diminta, kecepatan diperlukan pada titik B, C dan D. Mari kita analisis setiap bagian secara terpisah:

Bagian AB

Karena waktunya tidak tersedia di bagian ini, itu akan digunakan v_F² = v_{salah satu}² + 2nd.ΔX  Dengan vo = 0:

v_F² = 2a.Δx → v_F²= 2. 4,8 m/s² . 3 m = 28.8 m²/S² → v_F  = 5.37 m/s = v_B

Waktu yang dibutuhkan paket untuk melakukan perjalanan bagian AB adalah:

T_AB = (v_F - v_{salah satu}) /A = 5.37 m/s/4.8 m/s² = 1.19 s

Bagian BC

Kecepatan di bagian BC konstan, oleh karena itu v_B = v_C = 5.37 m/s. Waktu yang dibutuhkan paket untuk melakukan perjalanan bagian ini adalah:

Dapat melayani Anda: refraksi ringan: elemen, hukum dan percobaan

T_Bc = jarak _Bc  / v_B = 3 m/ 5.37 m/s = 0.56 s

Bagian CD

Kecepatan awal bagian ini adalah v_C = 5.37 m/s, Kecepatan terakhirnya v_D = 7.2 m/s, via v_D²  = v_C² + 2. ke. D Nilai dari D:

D = (v_D²  - v_C²)/2.a = (7.2²  - 5.37²)/2 X 4.8 m = 2.4 m

Waktu dihitung sebagai:

T_{CD =} (v_D  - v_C)/A = (7.2- 5.37)/ 4.8 S = 0.38 s.

Jawaban atas pertanyaan yang diajukan adalah:

a) d = 2.4 m

b) Waktu perjalanan T_AB + T_Bc + T_CD = 1.19 S +0.56 S +0.38 S = 2.13 s.

Contoh 2

Seseorang berada di bawah gerbang horizontal yang awalnya terbuka dan tinggi 12 m. Orang tersebut secara vertikal meluncurkan objek ke arah gerbang dengan kecepatan 15 m/s.

Diketahui bahwa gerbang ditutup 1,5 detik setelah orang tersebut meluncurkan objek dari ketinggian 2 meter. Resistensi udara tidak akan diperhitungkan. Jawab pertanyaan berikut, membenarkan:

a) Apakah Anda berhasil melewati objek melalui gerbang sebelum ditutup?

b) Apakah objek akan bertabrakan dengan gerbang tertutup? Jika afirmatif, kapan itu terjadi?

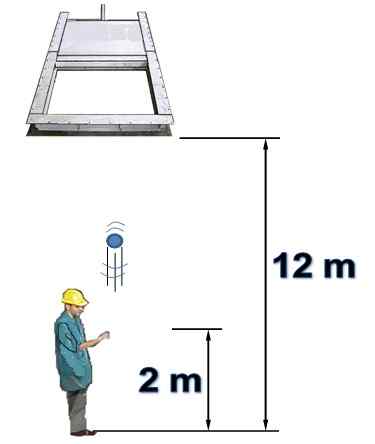Gambar 7. Suatu objek diluncurkan secara vertikal (Contoh 2). Sumber: Made sendiri.

Jawaban untuk)

Ada 10 meter antara posisi awal bola dan gerbang. Ini adalah peluncuran vertikal, di mana alamat ini dianggap positif.

Anda dapat mengetahui kecepatan yang dibawanya ketika Anda tiba pada titik ini, dengan hasil ini waktu yang diperlukan untuk melakukannya dan membandingkannya dengan waktu penutupan gerbang, yaitu 1.5 detik:

v_F ²= v_{salah satu} ²- 2.G. Δdan → v_F = (15² - 2 X 9.8 X10)^1/2 M = 5.39 m/s

T = (v_F - v_{salah satu}) /g = (5.39 - 15) / (-9.8) s = 0.98 s

Karena waktu ini kurang dari 1.5 detik, maka disimpulkan bahwa objek dapat melewati gerbang setidaknya sekali.

Jawab B)

Kami sudah tahu bahwa objek itu mengelola. Kecepatan, ketika mencapai pada ketinggian gerbang memiliki besarnya yang sama seperti saat naik, tetapi di arah yang berlawanan. Oleh karena itu bekerja dengan -5.39 m/s dan waktu yang diperlukan untuk mencapai situasi ini adalah:

T = (v_F - v_{salah satu}) /G = (-5.39 - 15) / (-9.8) S = 2.08 s

Karena gerbang tetap terbuka hanya untuk 1.5 detik, terbukti bahwa tidak punya waktu untuk lewat sebelum ditutup, karena ternyata ditutup. Jawabannya adalah: objek jika bertabrakan dengan gerbang tertutup setelah 2.08 detik setelah dirilis, saat turun.

Referensi

1. Figueroa, d. (2005). Seri: Fisika untuk Sains dan Teknik. Volume 1. Kinematika. Diedit oleh Douglas Figueroa (USB).69-116.
2. Giancoli, d. Fisika. (2006). Prinsip dengan aplikasi. 6^th Edisi. Prentice Hall. 22-25.
3. Kirkpatrick, l. 2007. Fisika: Pandangan Dunia. 6^ta Edisi Singkat. Pembelajaran Cengage. 23 - 27.
4. Resnick, r. (1999). Fisik. Volume 1. Edisi ketiga dalam bahasa Spanyol. Meksiko. Perusahaan Editorial Kontinental S.KE. dari c.V. 21-22.
5. Rex, a. (2011). Dasar -dasar fisika. Pearson. 33 - 36
6. Sears, Zemansky. 2016. Fisika Universitas dengan Fisika Modern. 14^th. Ed. Volume 1. 50 - 53.
7. Serway, r., Jewett, J. (2008). Fisika untuk Sains dan Teknik. Volume 1. 7^ma. Edisi. Meksiko. Editor Pembelajaran Cengage. 23-25.
8. Serway, r., Vulle, c. (2011). Dasar -dasar fisika. 9^na Ed. Pembelajaran Cengage. 43 - 55.
9. Wilson, J. (2011). Fisika 10. Pendidikan Pearson. 133 - 149.