Metode Hongaria Apa yang terdiri, contohnya

Dia Metode Hongaria Ini adalah algoritma yang digunakan dalam masalah alokasi saat Anda ingin meminimalkan biaya. Artinya, ini digunakan untuk menemukan biaya minimum dengan menugaskan beberapa orang ke berbagai kegiatan berdasarkan biaya terendah. Setiap kegiatan harus ditugaskan untuk orang yang berbeda.

Masalah penugasan adalah jenis khusus masalah pemrograman linier, di mana tujuannya adalah untuk meminimalkan biaya atau waktu menyelesaikan sejumlah pekerjaan oleh beberapa orang.

Sumber: Pixabay.com

Salah satu karakteristik penting dari masalah alokasi adalah bahwa hanya satu pekerjaan (atau pekerja) yang ditugaskan ke mesin (atau proyek).

Metode ini dikembangkan oleh ahli matematika Hongaria D. Konig. Untuk alasan ini, ini dikenal sebagai metode Hongaria untuk masalah alokasi. Ini juga dikenal sebagai algoritma penugasan kuhn-munkres.

Masalah alokasi apa pun dapat diselesaikan dengan mudah dengan menerapkan metode ini yang terdiri dari dua fase:

- Dengan fase pertama ada pengurangan baris dan pengurangan kolom.

- Pada fase kedua solusi pada basis berulang dioptimalkan.

[TOC]

Apa metode Hongaria?

Metode Hongaria terdiri dari empat langkah. Dua langkah pertama dieksekusi hanya sekali, sementara langkah 3 dan 4 diulangi sampai mereka menemukan tugas yang optimal.

Itu dianggap sebagai fakta masuk ke matriks kuadrat urutan n oleh n, yang hanya harus berisi elemen non -negatif.

Untuk masalah yang diberikan, jika jumlah baris dalam matriks tidak sama dengan jumlah kolom, baris fiktif atau kolom fiktif harus ditambahkan, tergantung pada kasingnya. Biaya penugasan untuk sel fiktif ini selalu ditugaskan sebagai nol.

Langkah 1: Kurangi minimum setiap baris

Untuk setiap baris matriks, elemen dipilih dengan nilai terendah dan pengurangan setiap elemen di baris itu.

Dapat melayani Anda: apa aset saat ini? (Dengan contoh)

Langkah 2: Kurangi minimum setiap kolom

Demikian pula, elemen dengan nilai terendah dipilih untuk setiap kolom dan menguranginya dari setiap elemen di kolom tersebut.

Langkah 3: Tutup semua nol dengan jumlah minimum garis

Semua nol harus dicakup dalam matriks yang dihasilkan dari langkah 2 menggunakan jumlah minimum garis horizontal dan vertikal, baik dengan baris atau kolom.

Jika total garis diperlukan untuk menutupi semua nol, menjadi n sama dengan ukuran n per n dari matriks, akan ada penugasan optimal antara nol dan oleh karena itu algoritma berhenti.

Kalau tidak, jika lebih sedikit garis diperlukan untuk menutupi semua nol dalam matriks, itu berlanjut dengan langkah 4.

Langkah 4: Buat nol tambahan

Elemen terkecil dari matriks (disebut k) dipilih yang tidak dicakup oleh salah satu garis yang dibuat pada langkah 3.

Nilai K dari semua elemen yang tidak dicakup oleh garis dikurangi. Selanjutnya, nilai k ditambahkan ke semua elemen yang dicakup oleh persimpangan dua baris.

Elemen -elemen yang ditutupi oleh satu garis dibiarkan seperti itu. Setelah melakukan langkah ini, Anda kembali ke langkah 3.

Penugasan optimal

Setelah algoritma dihentikan pada langkah 3, satu set nol dipilih sehingga setiap baris dan setiap kolom hanya memiliki satu nol yang dipilih.

Jika dalam proses seleksi ini tidak ada nol tunggal dalam satu baris atau kolom, salah satu nol tersebut kemudian akan dipilih. Nol yang tersisa dihilangkan di kolom atau baris itu, mengulangi hal yang sama untuk tugas lain juga.

Itu bisa melayani Anda: makrolokalisasi

Jika tidak ada alokasi tunggal nol berarti ada banyak solusi. Namun, biayanya akan tetap sama untuk set alokasi yang berbeda.

Setiap baris atau kolom fiktif yang telah ditambahkan dihilangkan. Zeros yang dipilih dalam matriks akhir ini sesuai dengan penugasan ideal yang diperlukan dalam matriks asli.

Contoh

Pertimbangkan sebuah perusahaan di mana ada empat kegiatan (A1, A2, A3, A4) yang harus dieksekusi oleh empat pekerja (T1, T2, T3, T4). Aktivitas per pekerja harus ditugaskan.

Matriks berikut menunjukkan biaya penugasan pekerja tertentu untuk kegiatan tertentu. Tujuan yang dikejar adalah untuk meminimalkan total biaya tugas yang terdiri dari empat kegiatan ini.

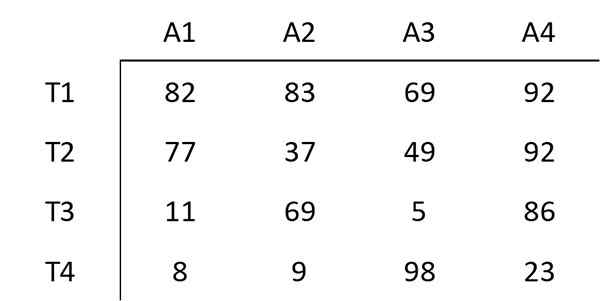
Langkah 1: Kurangi minimum setiap baris

Elemen dimulai dengan nilai minimum setiap baris elemen lain dari baris itu. Misalnya, elemen terkecil di baris pertama adalah 69. Oleh karena itu, 69 dari setiap elemen dikurangi di baris pertama. Matriks yang dihasilkan adalah:

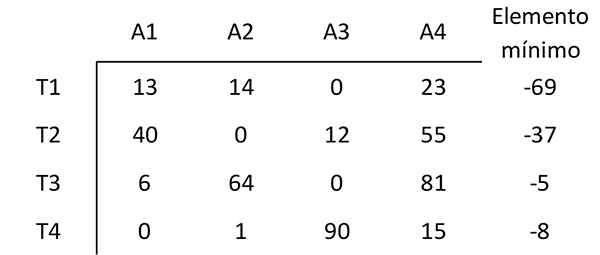
Langkah 2: Kurangi minimum setiap kolom

Dengan cara yang sama, elemen dikurangi dengan nilai minimum setiap kolom elemen lain dari kolom itu, memperoleh matriks berikut:

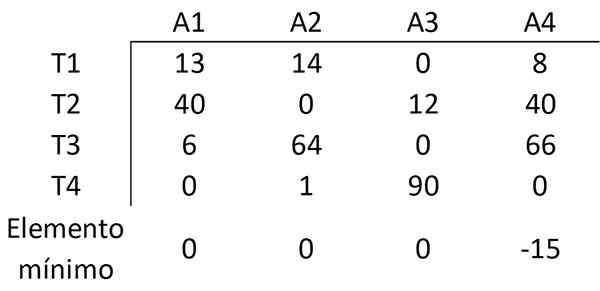
Langkah 3: Tutup semua nol dengan jumlah minimum garis

Sekarang jumlah minimum garis (horizontal atau vertikal) akan ditentukan yang diperlukan untuk menutupi semua nol dalam matriks. Semua nol dapat ditutupi menggunakan 3 baris:

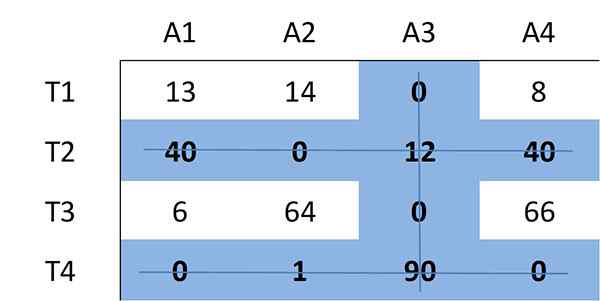
Karena jumlah garis yang dibutuhkan adalah tiga dan kurang dari ukuran matriks (n = 4), berlanjut dengan langkah 4.

Dapat melayani Anda: manajemen proyek: apa itu, fase, tujuan, contoh

Langkah 4: Buat nol tambahan

Elemen terendah yang tidak dicakup oleh garis dipilih, yang nilainya 6. Nilai ini dari semua elemen yang tidak terikat dikurangi dan nilai yang sama ini ditambahkan ke semua elemen yang dicakup oleh persimpangan dua baris. Ini menghasilkan matriks berikut:

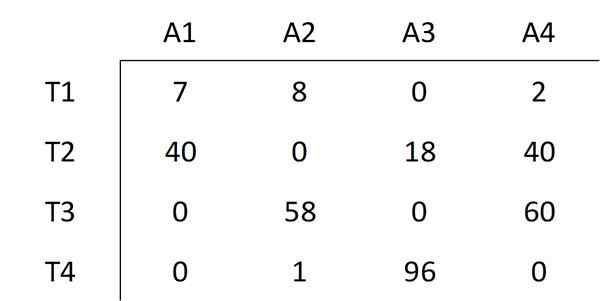
Seperti yang ditunjukkan dalam metode Hongaria, langkah nomor tiga harus dilakukan lagi.

Langkah 3 (Pengulangan)

Sekali lagi jumlah minimum jalur yang diperlukan untuk menutupi semua nol dalam matriks ditentukan. Kali ini diperlukan empat baris:

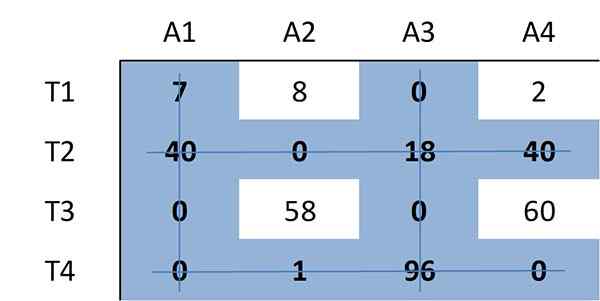
Karena jumlah garis yang dibutuhkan adalah 4, sama dengan ukuran matriks (n = 4), ada penugasan optimal antara nol dalam matriks. Oleh karena itu, algoritma berhenti.

Penugasan optimal

Seperti yang ditunjukkan oleh metode ini, pemilihan yang dibuat dari nol berikut sesuai dengan penugasan optimal:

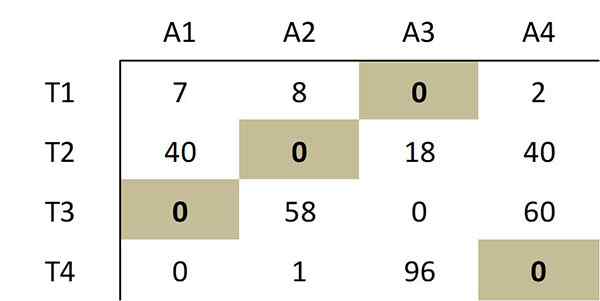
Pilihan nol ini sesuai dengan alokasi optimal berikut dalam matriks biaya asli:

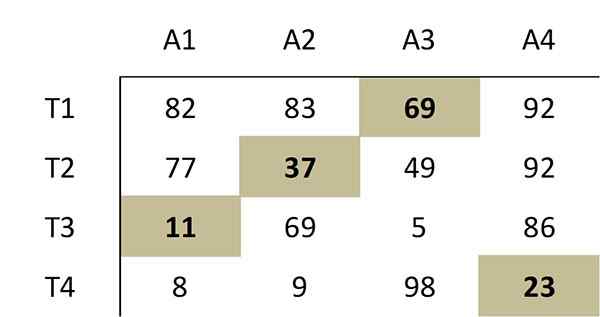
Oleh karena itu, pekerja 1 harus melakukan Kegiatan 3, Pekerja 2, Kegiatan 2, Pekerja 3, Kegiatan 1 dan Pekerja 4 harus melakukan Kegiatan 4. Total biaya penugasan optimal ini adalah 69+37+11+23 = 140.

Referensi

1. Algoritma Hongaria (2019). Algoritma Hongaria. Diambil dari: HungariaLgorithma.com.
2. Studi (2019). Menggunakan algoritma Hongaria untuk menyelesaikan masalah penugasan. Diambil dari: belajar.com.
3. Pekerjaan Kebijaksanaan (2018). Metode Hongaria untuk Memecahkan Masalah Penugasan - Teknik Kuantitatif untuk Manajemen. Diambil dari: WisdomJobs.com.
4. Geeks untuk Geeks (2019). Algoritma Hongaria untuk masalah penugasan. Diambil dari: geeksforgeeks.org.
5. Karleight Moore, Nathan Landman (2019). Algoritma pencocokan maksimum Hongaria. Cemerlang. Diambil dari: brilian.org.