Metodologi Pengambilan Sampel Acak, Keuntungan, Kekurangan, Contoh

Dia pengambilan sampel acak Ini adalah cara untuk memilih sampel yang representatif secara statistik dari populasi tertentu. Bagian dari prinsip bahwa setiap elemen sampel harus memiliki probabilitas yang sama untuk dipilih.

Undian adalah contoh pengambilan sampel acak, di mana setiap anggota populasi peserta diberi nomor. Untuk memilih angka yang sesuai dengan penghargaan undian (sampel) Beberapa teknik acak digunakan, misalnya ekstrak dari kotak surat angka yang dicetak pada kartu yang identik.

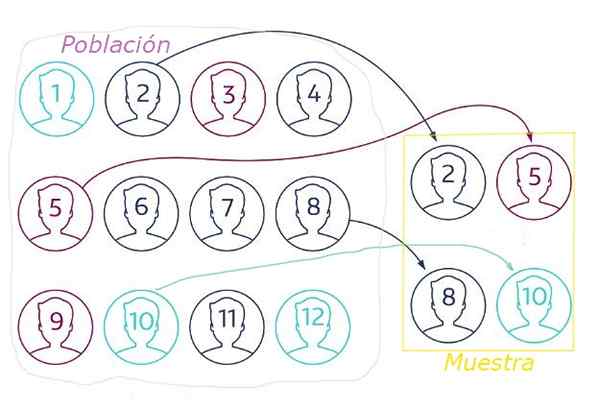Gambar 1. Dalam pengambilan sampel acak sampel diekstraksi dari populasi acak melalui beberapa teknik yang memastikan bahwa semua elemen memiliki probabilitas yang sama untuk dipilih. Sumber: NetQuest.com.

Dalam pengambilan sampel acak itu penting.

[TOC]

Ukuran sampel

Ada formula untuk menentukan ukuran sampel yang tepat. Faktor terpenting untuk dipertimbangkan adalah apakah ukuran populasi diketahui atau tidak. Mari kita lihat formula untuk menentukan ukuran sampel:

Kasus 1: Ukuran populasi tidak diketahui

Ketika ukuran populasi tidak diketahui, dimungkinkan untuk memilih sampel N yang memadai, untuk menentukan apakah hipotesis tertentu benar atau salah.

Untuk ini, formula berikut digunakan:

n = (z² P Q)/(e²)

Di mana:

-P Ini adalah probabilitas bahwa hipotesis itu benar.

-Q adalah probabilitas bahwa itu tidak, oleh karena itu q = 1 - p.

-E adalah margin kesalahan relatif, misalnya kesalahan 5% memiliki margin E = 0,05. 

-Z berkaitan dengan tingkat kepercayaan yang dibutuhkan oleh penelitian ini.

Dapat melayani Anda: distribusi normal: formula, karakteristik, contoh, olahraga

Dalam distribusi normal yang ditiru (atau dinormalisasi), tingkat kepercayaan 90% memiliki z = 1.645, karena probabilitas hasilnya adalah antara -1.645σ dan +1.645σ adalah 90%, di mana σ adalah standar deviasi.

Tingkat kepercayaan dan nilai z yang sesuai 

1.- Tingkat kepercayaan 50% sesuai dengan z = 0,675.

2.- 68.Tingkat kepercayaan 3% sesuai dengan z = 1.

3.- Level kepercayaan 90% setara dengan z = 1.645.

4.- Tingkat kepercayaan 95% sesuai dengan z = 1,96

5.- Tingkat kepercayaan 95,5% sesuai dengan z = 2.

6.- Tingkat kepercayaan 99,7% setara dengan z = 3.

Contoh di mana formula ini dapat diterapkan adalah dalam penelitian untuk menentukan berat rata -rata kerikil pantai.

Jelas tidak mungkin untuk mempelajari dan menimbang semua kerikil pantai, jadi nyaman.

Gambar 2. Untuk mempelajari karakteristik kerikil pantai, perlu memilih sampel acak dengan jumlah yang representatif. (Sumber: Pixabay)

Kasus 2: Ukuran populasi diketahui

Ketika angka n elemen yang membentuk populasi tertentu (atau alam semesta) diketahui, jika Anda ingin memilih dengan sampel acak sederhana sampel sampel yang signifikan secara statistik, ini adalah rumusnya: 

n = (z²p q n)/(n e² + Z²P Q)

Di mana:

-Z adalah koefisien yang terkait dengan tingkat kepercayaan.

-P adalah probabilitas keberhasilan hipotesis.

-Q adalah probabilitas kegagalan dalam hipotesis, p + q = 1.

-N adalah ukuran total populasi.

-E adalah kesalahan relatif dari hasil penelitian.

Contoh

Metodologi untuk mengekstraksi sampel sangat tergantung pada jenis studi yang diperlukan. Oleh karena itu, pengambilan sampel acak memiliki aplikasi yang tak terhitung jumlahnya:

Dapat melayani Anda: tanda -tanda pengelompokan

Survei dan Kuisioner

Misalnya dalam survei telepon, orang dipilih untuk dikonsultasikan oleh generator angka acak, berlaku untuk wilayah yang diteliti.

Jika Anda ingin menerapkan kuesioner kepada karyawan perusahaan besar, maka pemilihan responden dapat digunakan melalui nomor karyawan mereka, atau nomor kartu identitas mereka.

Nomor ini juga harus dipilih secara acak, menggunakan generator nomor acak misalnya.

Gambar 3. Kuesioner dapat diterapkan secara acak memilih peserta. Sumber: Pixabay.

Qa

Jika penelitian ini ada di bagian yang diproduksi oleh mesin, bagian harus dipilih secara acak, tetapi banyak yang dibuat pada waktu yang berbeda dalam sehari, atau dalam hari atau minggu yang berbeda.

Keuntungan

Contoh acak sederhana:

- Hal ini memungkinkan untuk mengurangi biaya studi statistik, karena tidak perlu mempelajari total populasi untuk mendapatkan hasil yang dapat diandalkan secara statistik, dengan tingkat kepercayaan yang diinginkan dan tingkat kesalahan yang diperlukan dalam penelitian ini.

- Hindari Bias: Karena pilihan elemen yang akan dipelajari sepenuhnya secara acak, penelitian ini dengan setia mencerminkan karakteristik populasi, meskipun hanya sebagian dari yang sama yang dipelajari.

Kerugian

- Metode ini tidak memadai dalam kasus yang ingin Anda ketahui preferensi dalam berbagai kelompok atau strata populasi.

Dalam hal ini lebih baik untuk menentukan kelompok atau segmen yang sebelumnya di mana studi dilakukan. Setelah strata atau kelompok telah ditentukan, maka jika lebih mudah bagi masing -masing untuk menerapkan pengambilan sampel acak.

- Sangat tidak mungkin bahwa informasi tentang sektor minoritas diperoleh, yang kadang -kadang perlu untuk mengetahui karakteristik mereka.

Dapat melayani Anda: aturan Simpson: formula, demonstrasi, contoh, latihan

Misalnya, jika itu adalah kampanye pada produk yang mahal, perlu mengetahui preferensi sektor minoritas terkaya.

Olahraga diselesaikan

Kami ingin mempelajari preferensi populasi dengan cara cola cola, tetapi tidak ada penelitian sebelumnya dalam populasi itu, di mana ukurannya tidak diketahui.

Di sisi lain, sampel harus representatif dengan tingkat kepercayaan minimum 90% dan kesimpulan harus memiliki persentase kesalahan 2%.

-Bagaimana menentukan ukuran S sampel?

-Apa ukuran sampel jika margin kesalahan dibuat hingga 5%?

Larutan

Karena ukuran populasi tidak diketahui, untuk menentukan ukuran sampel, formula yang diberikan di atas digunakan:

n = (z²P Q)/(e²)

Kami mengasumsikan bahwa ada probabilitas preferensi yang sama (p) dengan penyegaran kami dari non -preferensi (q), maka p = q = 0,5.

Di sisi lain, karena hasil penelitian harus memiliki kesalahan persentase kurang dari 2%, maka kesalahan relatif akan 0,02.

Akhirnya, nilai z = 1.645 menghasilkan tingkat kepercayaan 90%.

Singkatnya, Anda memiliki nilai -nilai berikut:

Z = 1.645

P = 0,5

Q = 0,5

E = 0,02

Dengan data ini ukuran sampel minimum dihitung:

N = (1.645² 0,5 0,5)/(0,02²) = 1691.3

Ini berarti bahwa studi dengan margin kesalahan yang diperlukan dan dengan tingkat kepercayaan yang dipilih, harus memiliki sampel responden setidaknya 1692 individu, dipilih dengan pengambilan sampel acak sederhana.

Jika Anda beralih dari margin kesalahan dari 2% menjadi 5%, maka ukuran sampel baru adalah:

N = (1.645² 0,5 0,5)/(0,05²) = 271

Yang merupakan jumlah individu yang jauh lebih rendah. Kesimpulannya, ukuran sampel sangat sensitif terhadap margin yang diinginkan dalam penelitian ini.

Referensi

1. Berenson, m. 1985.Statistik untuk Administrasi dan Ekonomi, Konsep dan Aplikasi. Inter -American Editorial.
2. Statistik. Pengambilan sampel acak. Diambil dari: ensiklopedia ekonomi.com.
3. Statistik. Contoh. Pulih dari: statistik.Tikar.USON.MX.
4. Dieksplorasi. Pengambilan sampel acak. Dipulihkan dari: Dieksplorasi.com.
5. Moore, d. 2005. Statistik dasar diterapkan. 2nd. Edisi.
6. NetQuest. Pengambilan sampel acak. Pulih dari: netquest.com.
7. Wikipedia. Sampel statistik. Diperoleh dari: di.Wikipedia.org