Sudut Terdaftar dari Definisi Lingkaran, Teorema, Contoh

Dia Sudut Terdaftar Lingkaran Itu adalah salah satu yang memiliki simpul di lingkar dan semi -langsung kering atau bersinggungan. Akibatnya sudut terdaftar akan selalu cembung atau datar.

Pada Gambar 1 beberapa sudut yang terdaftar di sirkumferasi masing -masing diwakili. Sudut ∠Edf terdaftar dengan memiliki simpul D pada keliling dan dua semi -recrensing [dari) dan [df) mengeringkan lingkar. 

Gambar 1. Beberapa sudut tertulis tentang kelilingnya masing -masing. Sumber: f. Zapata dengan Geogebra.

Demikian pula, sudut ∠HGI terdaftar, karena memiliki simpulnya di lingkar dan sisi keringnya yang sama.

Sudut ∠kjr dan ∠ust juga terdaftar di lingkar. Yang pertama memiliki satu sisi penjahitan dan garis singgung lainnya, sedangkan yang kedua memiliki dua sisi garis singgung ke lingkar, membentuk sudut bidang datar (180º).

Beberapa penulis menyebut sudut semi-terjepit kepada orang yang memiliki salah satu sisi yang bersinggungan dengan lingkar, tetapi dalam artikel ini ia dianggap terdaftar.

Setiap sudut terdaftar mendefinisikan atau mengganti busur yang terkait dengan hal yang sama. Misalnya pada Gambar 2 sudut terdaftar ∠ABC menggantikan busur A⌒C dengan panjang d.

Gambar yang sama menunjukkan sudut ∠doe, yang tidak terdaftar di lingkar karena tidak memiliki simpulnya di lingkar, tetapi di tengah atau.

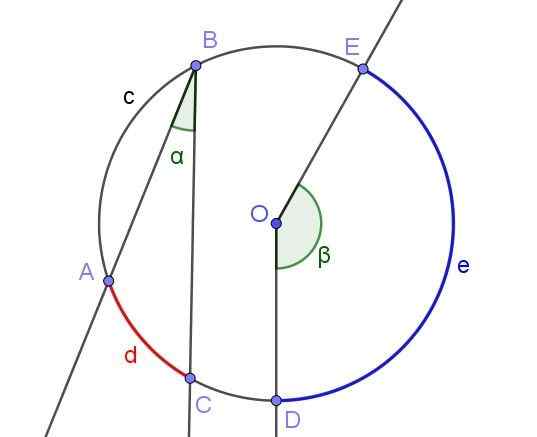Gambar 2. Sudut Terdaftar ∠ABC dan sudut pusat ∠doe. Sumber: f. Zapata dengan Geogebra.

[TOC]

Sudut tengah

Selain sudut terdaftar, sudut tengah, yang merupakan orang yang simpulnya berada di tengah keliling dan yang sisi -sisinya dipotong ke lingkar.

Dapat melayani Anda: perbedaan antara fraksi umum dan angka desimal

Ukuran radianes dari sudut pusat adalah hasil bagi antara busur yang subtends, yaitu, keliling busur antara sisi sudut, dan jari -jari keliling keliling.

Jika kelilingnya adalah kesatuan (jari -jari 1), maka panjang busur dalam unit radio yang sama adalah ukuran sudut dalam radianes.

Dan ketika ukuran sudut diperlukan dalam derajat, maka ukuran dikalikan dalam radian dengan faktor 180º/π.

Instrumen pengukuran sudut selalu menggunakan sudut pusat dan panjang busur yang digantikan oleh ini secara langsung dikalibrasi dalam derajat. Ini berarti bahwa setiap kali sudut diukur, di latar belakang yang diukur adalah panjang busur yang digantikan oleh sudut tengah.

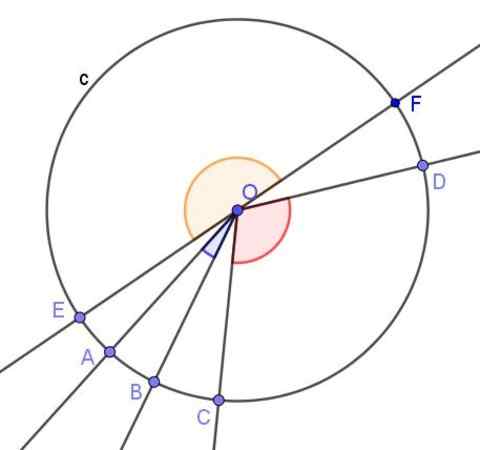Gambar 3. Beberapa sudut sentral dari lingkar. Sumber: f. Zapata dengan Geogebra.

Teorema

- Teorema 1 (sudut terdaftar dan sudut tengah)

Ukuran sudut terdaftar adalah setengah dari ukuran sudut tengah, jika kedua sudutnya subtit busur yang sama.

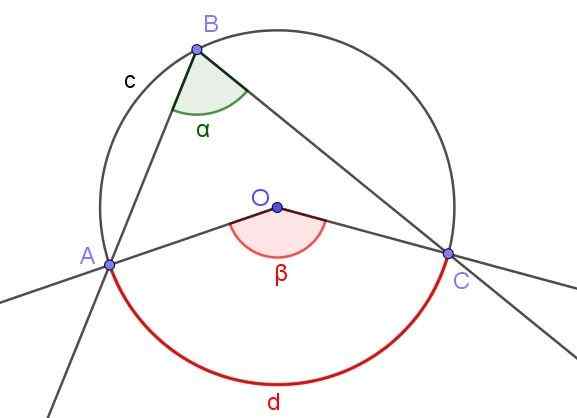Gambar 4. Sudut Terdaftar ∠ABC dan sudut pusat ∠AOC yang subtit ARC A⌒C yang sama. Sumber: f. Zapata dengan Geogebra.

Gambar 4 menunjukkan dua sudut ∠ABC dan ∠AOC, yang memotong keliling keliling yang sama.

Jika ukuran sudut terdaftar adalah α, maka ukuran β dari sudut pusat adalah dua kali ukuran sudut terdaftar (β = 2 α) karena keduanya mengurangi busur yang diukur yang sama.

Demonstrasi 1

Untuk menunjukkan Teorema 1, beberapa kasus tertentu akan dimulai, sampai mencapai kasus umum.

Dapat melayani Anda: Hukum Sandwich: Penjelasan dan Latihan

Misalkan sudut terdaftar, di mana salah satu sisinya melewati pusat keliling, seperti yang ditunjukkan pada Gambar 5.

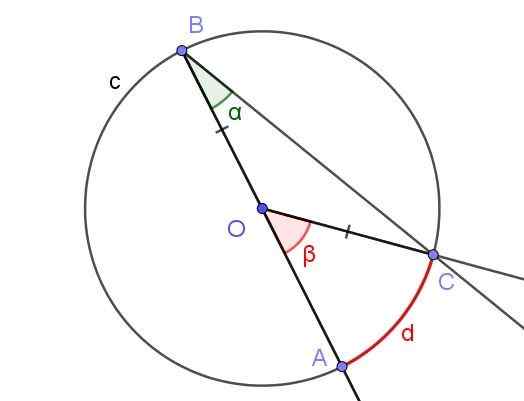Gambar 5. Sudut Terdaftar ∠ABC dengan sisi [BA) melalui O dan sudut tengah ∠AOC. Sumber: f. Zapata dengan Geogebra.

Dalam hal ini, COB Isosceles Triange terbentuk, karena [OC] = [OB].

Dalam segitiga Isosceles, sudut yang berdekatan dengan pangkalan adalah sama, oleh karena itu mereka harus ∠BCO = ∠ABC = α. Di sisi lain ∠cob = 180º - β.

Mempertimbangkan jumlah sudut internal segitiga Cob yang Anda miliki:

α + α + (180º - β) = 180º

Di mana ia mengikuti bahwa 2 α = β, atau apa yang setara: α = β/2. Ini bertepatan dengan Teorema 1 apa: Ukuran sudut terdaftar adalah setengah dari sudut tengah, jika kedua sudutnya mengirimkan tali yang sama [AC].

Demonstrasi 1b

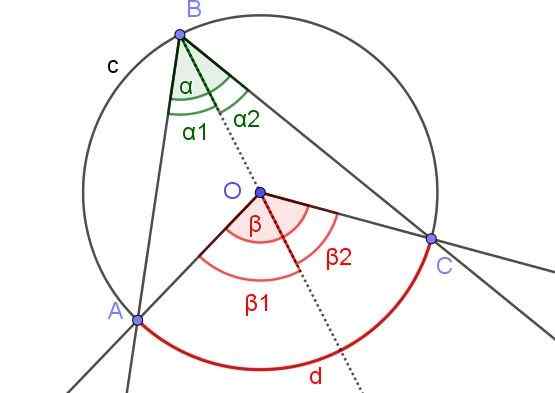Gambar 6. Konstruksi tambahan untuk menunjukkan bahwa α = β/2. Sumber: f. Zapata dengan Geogebra.

Dalam hal ini ada sudut yang tertulis ∠ABC, di mana pusat atau keliling berada di dalam sudut.

Untuk menunjukkan Teorema 1 dalam hal ini, tambahan Auxiliary [BO) ditarik, sehingga ada dua sudut terdaftar ∠ABO dan ∠OBC berdekatan dengan semi -recreational.

Demikian pula mereka memiliki sudut pusat β₁ dan β₂ berdekatan dengan semi -direkreasi. Dengan cara ini Anda memiliki situasi yang sama seperti dalam Demonstrasi 1, sehingga dapat dinyatakan bahwa α₂ = β₂ /2 dan α₁ = β₁ /2. Seperti α = α₁ + α₂ dan β = β₁ + β₂ Karena itu ada α = α₁ + α₂ = β₁ /2 + β₂ /2 = (β₁ + β₂) / 2 = β / 2.

Dapat melayani Anda: jenis integral

Kesimpulan α = β / 2, yang memenuhi teorema 1.

- Teorema 2

Jika dua atau lebih sudut terdaftar menggantikan busur yang sama, maka mereka memiliki ukuran yang sama.

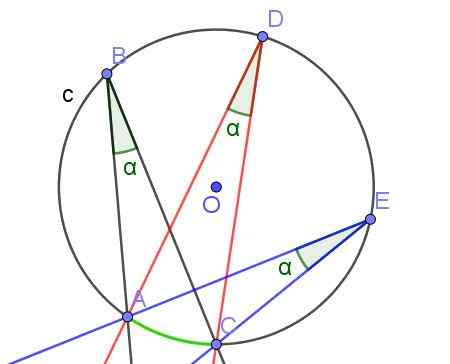Gambar 7. Sudut terdaftar dengan ukuran yang sama α, karena mereka menggantikan busur yang sama. Sumber: f. Zapata dengan Geogebra.

- Teorema 3

Subtit sudut terdaftar ada string dengan ukuran yang sama adalah sama.

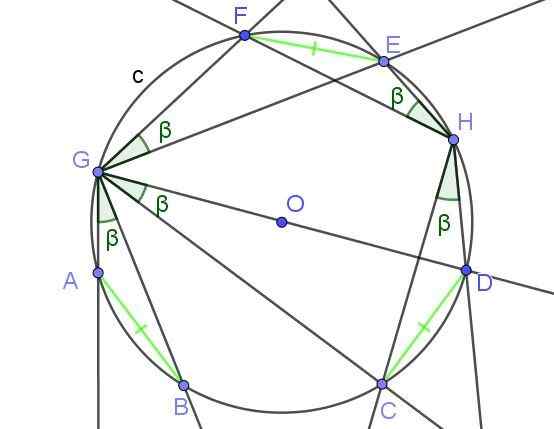Angka 8. Sudut yang tertulis dengan tali subtuse dengan ukuran yang sama, memiliki ukuran yang sama β. Sumber: f. Zapata dengan Geogebra.

Contoh

- Contoh 1

Menunjukkan bahwa sudut yang tertulis subtit diameter adalah sudut kanan.

Larutan

Sudut pusat ∠AOB yang terkait dengan diameter adalah sudut datar, yang ukurannya adalah 180º.

Menurut Teorema 1, sudut apa pun yang terdaftar di lingkar yang menggantikan tali yang sama (dalam hal ini diameter), memiliki pengukuran setengah dari sudut tengah yang subtit tali yang sama, yang untuk contoh kami adalah 180º/2 = 90º.

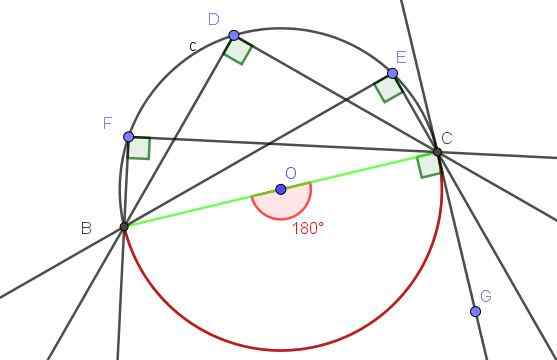Gambar 9. Sudut terdaftar apa pun yang subtends ke diameter adalah sudut kanan. Sumber: f. Zapata dengan Geogebra.

- Contoh 2

Garis (BC) singgung dalam A A ke lingkar C, menentukan sudut yang tertulis ∠BAC (lihat Gambar 10).

Pastikan bahwa Teorema 1 dari sudut terdaftar terpenuhi.

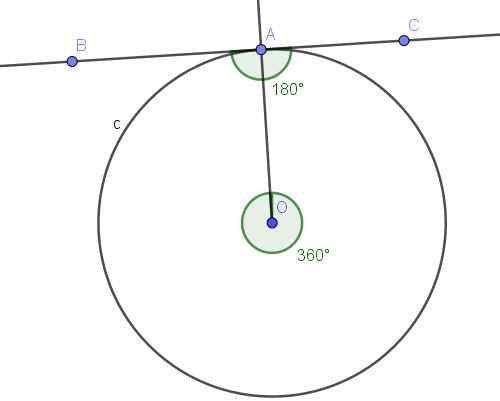Gambar 10. Bac sudut terdaftar dan sudut sentral cembungnya AOA. Sumber: f. Zapata dengan Geogebra.

Larutan

Sudut ∠BAC terdaftar karena simpulnya ada di lingkar, dan sisi -sisinya [ab) dan [ac) bersinggungan dengan keliling, sehingga definisi sudut tertulis terpenuhi.

Di sisi lain, sudut tertulis ∠BAC menggantikan lengkungan A⌒a, yang merupakan keliling lengkap. Sudut pusat yang menggantikan lengkungan A⌒A adalah sudut cembung yang ukurannya adalah sudut penuh (360º).

Sudut terdaftar subtit busur penuh mengukur setengah dari sudut pusat yang terkait, yaitu, ∠bac = 360º/2 = 180º.

Dengan semua hal di atas terbukti bahwa kasus khusus ini memenuhi Teorema 1.

Referensi

1. Baldor. (1973). Geometri dan Trigonometri. Editorial Budaya Amerika Tengah.
2. DAN. KE. (2003). Elemen Geometri: Dengan Latihan dan Geometri Kompas. Universitas Medellin.
3. Geometri 1. Sudut di lingkar. Pulih dari: edu.Xunta.adalah/
4. Semua sains. Latihan Sudut yang Diusulkan di Lingkar. Pulih dari: francesphysics.Blogspot.com
5. Wikipedia. Sudut terdaftar. Pulih dari: is.Wikipedia.com