Nomor Euler atau Nomor E Berapa Banyak Nilai, Properti, Aplikasi

Dia Nomor atau nomor euler e Ini adalah konstanta matematika yang terkenal yang sering muncul dalam berbagai aplikasi ilmiah dan ekonomi, bersama dengan angka π dan angka penting lainnya dalam matematika.

Kalkulator ilmiah melempar nilai berikut untuk angka e:

Gambar 1. Nomor Euler sering muncul dalam sains. Sumber: f. Zapata.

E = 2.718281828…

Tetapi lebih banyak desimal yang diketahui, misalnya:

E = 2.71828182845904523536…

Dan komputer modern telah memungkinkan triliun desimal ke angka e.

Itu adalah angka irasional, Yang berarti memiliki jumlah desimal yang tak terbatas tanpa pola berulang (urutan 1828 muncul dua kali di awal dan tidak lagi diulang).

Dan itu juga berarti bahwa angka E tidak dapat diperoleh sebagai hasil bagi dari dua bilangan bulat.

[TOC]

Sejarah

Nomor Dan Dia diidentifikasi oleh ilmuwan Jacques Bernoulli pada tahun 1683 ketika dia mempelajari masalah minat majemuk, tetapi sebelumnya dia secara tidak langsung muncul dalam karya matematikawan Skotlandia John Napier, yang menemukan logaritma untuk 1618.

Namun, Leonhard Euler pada tahun 1727 yang memberinya nama nomor E dan secara intensif mempelajari propertinya. Itulah mengapa juga dikenal sebagai Nomor Euler dan juga sebagai dasar alami untuk logaritma Neperian (eksponen) yang digunakan.

Berapa nilai E?

Nomor E Vale:

E = 2.71828182845904523536…

Poin suspensi berarti bahwa ada sejumlah besar desimal dan pada kenyataannya, jutaan dari mereka dikenal dengan komputer saat ini.

Representasi angka e

Ada beberapa cara untuk mendefinisikan E yang kami jelaskan di bawah ini:

Angka E sebagai batas

Salah satu dari berbagai cara di mana angka E diekspresikan adalah salah satu yang ditemukan oleh ilmuwan Bernoulli dalam karyanya tentang bunga majemuk:

Di mana Anda harus melakukan nilainya N jumlah yang sangat besar.

Mudah untuk memeriksa, dengan bantuan kalkulator, saat itu N Ini sangat besar, ekspresi sebelumnya cenderung ke nilai Dan diberikan di atas.

Itu dapat melayani Anda: fungsi bijyjective: apa itu, bagaimana cara melakukannya, contoh, latihan

Tentu saja kita bisa bertanya pada diri sendiri seberapa besar itu bisa dilakukan N, Jadi kami mencoba dengan nomor bundar, seperti ini misalnya:

n = 1000; 10.000 atau 100.000

Dalam kasus pertama Anda mendapatkan E = 2.7169239… . Di E kedua = 2.7181459 ... dan di yang ketiga jauh lebih dekat dengan nilai Dan: 2.7182682. Kita sudah bisa tampil dengan n = 1.000.000 atau lebih besar, pendekatannya akan lebih baik.

Dalam bahasa matematika, prosedur pembuatan N Itu semakin dekat dan lebih ke nilai yang sangat besar, disebut batas untuk tak terbatas Dan itu dilambangkan seperti ini:

Untuk menunjukkan tak terbatas, simbol "∞" digunakan.

Angka E sebagai jumlah

Dimungkinkan juga untuk mendefinisikan angka E melalui operasi ini:

Angka -angka yang muncul dalam penyebut: 1, 2, 6, 24, 120 ... sesuai dengan operasi N!, Di mana:

N! = n. (N-1).(N-2). (N-3) ..

Dan menurut definisi 0! = 1.

Mudah untuk memverifikasi bahwa semakin banyak penambahan ditambahkan, semakin besar jumlahnya tercapai Dan.

Mari kita lakukan beberapa tes dengan kalkulator, menambahkan lebih banyak tambahan:

1 +1+ (1/2) + (1/6) = 2.71667

1 +1+ (1/2) + (1/6) + (1/24) = 2.75833

1 +1+ (1/2) + (1/6) + (1/24) + (1/120) = 2.76667

1 +1+ (1/2) + (1/6) + (1/24) + (1/120) + (1/720) = 2.71806

Semakin banyak istilah mereka ditambahkan ke jumlah, semakin banyak hasilnya mirip Dan.

Matematikawan merancang notasi ringkas untuk jumlah ini yang melibatkan banyak istilah, menggunakan simbol jumlah σ:

Ekspresi ini dibaca sebagai "jumlah n = 0 hingga tak terbatas dari 1 antara n faktorial".

Angka E dari sudut pandang geometris

Angka E memiliki representasi grafik yang terkait dengan area di bawah grafik kurva:

y = 1/x

Ketika nilai -nilai x adalah antara 1 dan E, area ini bernilai 1, seperti yang diilustrasikan dalam gambar berikut:

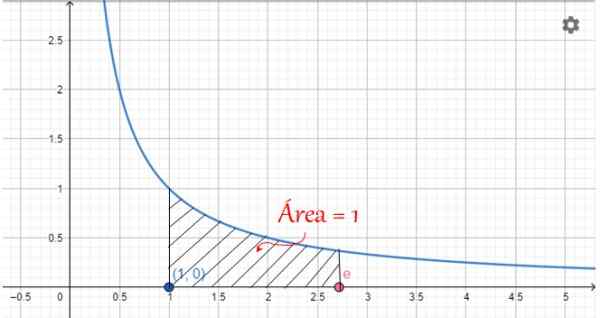Gambar 2. Representasi grafis angka E: Area di bawah kurva 1/x, antara x = 1 dan x = e O'Clock. Sumber: f. Zapata.

Nomor E Properties

Beberapa sifat angka E adalah:

Dapat melayani Anda: Fungsi Tumbuh: Cara Mengidentifikasi, Contoh, Latihan

-Dengan kata lain tidak rasional, tidak dapat diperoleh hanya dengan membagi dua bilangan bulat.

-Nomor Dan Itu juga a Nomor transenden, yang berarti itu Dan Ini bukan solusi dari persamaan polinomial apa pun.

-Ini terkait dengan empat angka terkenal lainnya di bidang matematika, yaitu: π, i, 1 dan 0, melalui identitas euler:

Dan^πi + 1 = 0

-Panggilan bilangan kompleks dapat diungkapkan melalui E.

-Ini merupakan dasar logaritma alami atau Neperian hari ini (definisi asli John Napier sedikit berbeda).

-Ini adalah satu -satunya angka sehingga logaritma Neperiannya bernilai 1, yaitu:

 ln e = 1

Aplikasi

Statistik

Jumlah E muncul sangat sering di bidang probabilitas dan statistik, muncul dalam berbagai distribusi, seperti normal atau Gaussian, yaitu Poisson dan lainnya.

Rekayasa

Dalam rekayasa itu sering terjadi, karena fungsi eksponensial y = e^X Ini ada dalam mekanika dan elektromagnetisme, misalnya. Di antara banyak aplikasi yang dapat kami kutip:

-Kabel atau rantai yang tergantung pada ujungnya, mengadopsi bentuk kurva yang diberikan oleh:

y = (e^X + Dan^-X) /2

-Kondensor C awalnya keluar, yang terhubung secara seri ke resistansi R dan sumber tegangan V untuk memuat, memperoleh beban q tertentu tergantung pada waktu yang diberikan oleh:

Q (t) = cv (1-e^-T/rc)

biologi

Fungsi eksponensial y = a.Dan^Bx, Dengan konstanta A dan B, ini digunakan untuk memodelkan pertumbuhan sel dan pertumbuhan bakteri.

Fisik

Dalam fisika nuklir, peluruhan radioaktif dan penentuan usia dimodelkan dengan radiokarbon tertanggal.

Ekonomi

Dalam perhitungan bunga gabungan, jumlah E muncul secara alami.

Misalkan Anda memiliki sejumlah uang P_{salah satu}, untuk menginvestasikannya pada tingkat bunga tahunan.

Jika uang dibiarkan selama 1 tahun, setelah waktu itu Anda akan memiliki:

P (1 tahun) = p_{salah satu} + P_{salah satu}.i = p_{salah satu} (1+ I)

Setelah satu tahun lagi tanpa menyentuhnya, Anda akan memiliki:

Dapat melayani Anda: probabilitas teoretis: cara mengeluarkannya, contoh, latihan

P (2 tahun) = p_{salah satu} + P_{salah satu}.i + (p_{salah satu} + P_{salah satu} .i) i = p_{salah satu} +2 p_{salah satu}.i + p_{salah satu}.yo²  = PO (1+i)²

Dan dengan cara ini N bertahun-tahun:

P = p_{salah satu} (1+i)^N

Sekarang ingat salah satu definisi E:

Ini terlihat seperti ekspresi untuk p, jadi pasti ada hubungan.

Kami akan mendistribusikan tingkat bunga nominal yo di dalam N Periode waktu, dengan cara ini tingkat bunga majemuk adalah I/N:

P = p_{salah satu} [1+ (I/N)]^N

Ekspresi ini terlihat sedikit lebih banyak tentang batas kami, tetapi belum persis sama.

Namun, setelah beberapa manipulasi aljabar dapat ditunjukkan bahwa membuat perubahan variabel ini:

h = n/i → i = n/jam

Uang kita menjadi:

P = p_{salah satu} [1+ (1/jam)]^Hai = P_{salah satu} [1+ (1/jam)]^Hyo

Dan apa yang ada di antara kunci, bahkan jika itu ditulis dengan surat itu H, Itu sama dengan argumen batas yang mendefinisikan angka E, hilang hanya mengambil batas.

Mari lakukan  H → ∞, dan apa yang ada di antara tombol diubah menjadi angka Dan. Ini tidak berarti bahwa kita harus menunggu waktu yang sangat besar untuk menarik uang kita.

Jika kita terlihat bagus, saat melakukan H = n/i Dan cenderung ∞, apa yang telah kita lakukan adalah mendistribusikan tingkat bunga dalam periode waktu yang sangat, sangat kecil: sangat kecil:

I = n/h

Ini disebut Kapitalisasi Berkelanjutan. Dalam hal ini, jumlah uang mudah dihitung sebagai berikut:

P = p_{salah satu} .Dan^yo

Dimana saya adalah tingkat bunga tahunan. Misalnya, dengan menyetor € 12 hingga 9 % per tahun, melalui kapitalisasi berkelanjutan, setelah satu tahun Anda memiliki:

P = 12 x e^{0.09 × 1} € = 13.€ 13

Dengan keuntungan 1.13 €.

Referensi

1. Nikmati matematika. Bunga majemuk: komposisi berkala. Pulih dari: nikmatiMaticaticas.com.
2. Figuera, J. 2000. Matematika 1. Diversifikasi. Edisi Co-Bo.
3. Garcia, m. Angka E dalam perhitungan dasar. Pulih dari: matematika.Ciens.UCV.pergi.
4. Jiménez, r. 2008. Aljabar. Prentice Hall.
5. Larson, r. 2010. Perhitungan variabel. 9NA. Edisi. Bukit McGraw.