Angka kuantum untuk apa gunanya dan apa itu

Itu NUmeter kuantum Mereka digunakan untuk menggambarkan keadaan kuantum elektron dalam atom dan berasal dari larutan persamaan Schrödinger untuk yang paling sederhana: hidrogen.

Persamaan Schrödinger adalah persamaan diferensial, yang solusinya Fungsi gelombang dan mereka dilambangkan dengan surat Yunani ψ. Solusi tak terbatas dapat dinaikkan, dan kuadratnya setara dengan probabilitas menemukan elektron di daerah kecil ruang, yang disebut orbital.

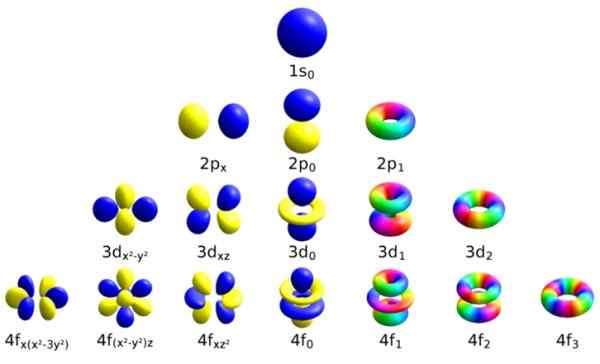
Masing -masing orbital atom ini dibedakan dengan set kuantum tertentu. Sumber: Wikimedia Commons.

Setiap orbital telah mendefinisikan karakteristik yang membedakannya dari yang lain, seperti energi, momentum sudut dan putaran, sifat kuantum yang sepenuhnya elektron dan yang bertanggung jawab, antara lain, untuk efek magnetik.

Cara mengidentifikasi setiap orbital adalah dengan membedakannya melalui serangkaian angka yang menggambarkannya, dan ini adalah angka kuantum yang tepat:

-N: adalah angka kuantum utama.

-ℓ: Angka kuantum azimutal.

-M_ℓ, Itu adalah angka magnetik.

-M_S, Nomor putaran.

[TOC]

Untuk apa angka kuantum?

Angka kuantum berfungsi untuk menggambarkan keadaan elektron di dalam atom. Model atom di mana elektron berbalik di sekitar nukleus tidak akurat, karena tidak konsisten dengan stabilitas atom atau dengan sejumlah besar fenomena fisik yang diamati.

Itulah sebabnya Denmark Niels Bohr (1885-1962) dibuat pada tahun 1913 proposal yang berani: elektron hanya dapat ditemukan dalam orbit stabil tertentu, yang ukurannya tergantung pada nomor integer yang disebut n n.

Kemudian, pada tahun 1925, fisik Austria Erwin Schrödinger (1887-1961) mengangkat persamaan diferensial dalam turunan parsial, yang solusinya menggambarkan atom hidrogen. Adalah fungsi gelombang ψ yang disebutkan di awal.

Persamaan diferensial ini mencakup tiga koordinat spasial plus waktu, tetapi ketika tidak termasuk, solusi dari persamaan Schrödinger analog dengan gelombang stasioner (gelombang yang menyebar di antara batas tertentu).

Fungsi gelombang

Persamaan waktu independen Schrödinger diselesaikan dalam koordinat bola dan solusinya ditulis sebagai produk dari tiga fungsi, satu untuk setiap variabel spasial. Dalam sistem koordinat ini, alih -alih menggunakan koordinat sumbu cartesian X, Dan Dan z Koordinat digunakan R, θ Dan φ. Cara ini:

Dapat melayani Anda: sirkuit paralel

ψ (r, θ, φ) = r (r) ⋅f (θ) ⋅g (φ)

Fungsi gelombang tidak berwujud, meskipun mekanika kuantum memberi tahu kita bahwa amplitudo persegi:

| ψ (r, θ, φ) |²

Yaitu, bahwa modul atau nilai absolut dari fungsi gelombang, kuadrat, adalah bilangan real yang mewakili probabilitas menemukan elektron, di wilayah tertentu di sekitar titik yang koordinatnya adalah R, θ Dan φ.

Dan fakta ini adalah sesuatu yang lebih konkret dan nyata.

Untuk menemukan fungsi gelombang, Anda harus menyelesaikan tiga persamaan diferensial biasa, satu untuk setiap variabel R, θ Dan φ.

Solusi dari masing -masing persamaan, yang akan menjadi fungsi r (r), f (θ) dan g (φ), berisi tiga angka kuantum pertama yang disebutkan.

Berapa angka kuantum?

Di bawah ini kami menggambarkan secara singkat sifat dari setiap nomor kuantum. Tiga yang pertama, seperti yang dinyatakan di atas, muncul dari solusi persamaan Schrödinger.

Angka keempat ditambahkan oleh Paul Dirac (1902 - 1984) pada tahun 1928.

Nomor kuantum utama

Itu dilambangkan dengan N dan menunjukkan ukuran orbital yang diizinkan, serta energi elektron. Semakin tinggi nilainya, semakin banyak elektron nukleus dan energinya juga akan, tetapi sebagai imbalannya mengurangi stabilitasnya.

Jumlah ini muncul dari fungsi R (R), yang merupakan probabilitas menemukan elektron pada jarak tertentu R inti, yang ditentukan oleh:

 Di mana konstanta berikut berpartisipasi:

-Planck Constant: h = 6.626 × 10 ^{-3. 4} J.S
-Massa elektron m_Dan = 9.1 × 10^-31 kg
-Beban elektron: e = 1.6 × 10^-19 C.
-Konstanta Elektrostatik: K = 9 × 10 ⁹ N.M²/C²

Ketika n = 1 sesuai dengan jari -jari bohr yang bernilai sekitar 5.3 × 10⁻¹¹ M.

Kecuali untuk lapisan pertama, yang lain dibagi lagi menjadi subkap atau sub -level. Setiap lapisan memiliki energi dalam elektron volt yang diberikan oleh:

Dapat melayani Anda: Gelombang Mekanik: Karakteristik, Properti, Rumus, Jenis

Syarat Ev "Elektron Volt" berarti, unit energi sering digunakan di area fisika kuantum. Dimana n = 1, 2, 3, 4 .. . dan setiap nilai n sesuai dengan a lapisan, yang diberi label dengan huruf kapital:

• K (n = 1)
• L (n = 2)
• M (n = 3)
• N (n = 4)
• Atau (n = 5)
• P (n = 6)
• Q (n = 7).

Secara teori tidak ada batas atas untuk n, tetapi dalam praktiknya diamati bahwa itu hanya mencapai n = 8. Energi yang paling tidak mungkin sesuai dengan n = 1 dan dari Negara mendasar.

Nomor kuantum azimutal atau momentum sudut

Dilambangkan dengan huruf miring, angka ini menentukan bentuk orbital, saat mengukur besarnya momentum sudut orbital elektron.

Anda dapat mengambil seluruh nilai dan positif antara 0 dan n-1, misalnya:

-Saat n = 1, lalu ℓ = 0 dan ada satu sub -level.

-Jika n = 2, maka ℓ bisa bernilai 0 atau 1, jadi Anda memiliki dua sub -level.

-Dan jika n = 3, maka ℓ mengasumsikan nilai 0, 1 dan 2 dan ada 3 sub -level.

Itu dapat diikuti tanpa batas waktu, meskipun seperti yang dinyatakan sebelumnya, dalam praktiknya n mencapai hingga 8. Sub -level dilambangkan melalui surat: S, P, D, F Dan G Dan mereka semakin meningkat energi.

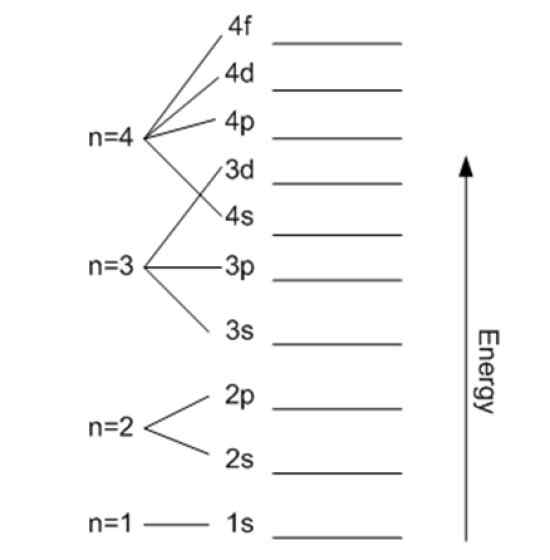Energi terkait dengan angka kuantum utama. Sumber: Wikimedia Commons.

Angka kuantum magnetik m_ℓ

Angka ini memutuskan orientasi orbital di ruang dan nilainya tergantung pada ℓ.

Untuk ℓ yang diberikan, ada (2ℓ+1) keseluruhan nilai m _ℓ, sesuai dengan orbital masing -masing. Ini adalah:

-ℓ, ( - ℓ+1),… 0,… (+ℓ -1),+ℓ.

Contoh

Jika n = 2, kita tahu bahwa ℓ = 0 dan ℓ = 1, maka m _ℓ Ambil nilai -nilai berikut:

-Untuk ℓ = 0: m _ℓ = 0.
-Untuk ℓ = 1: m _ℓ = -1, m _ℓ = 0, m _ℓ = +1

Orbital n = 2 memiliki dua sub -level, yang pertama dengan n = 2, ℓ = 0 dan m _ℓ = 0. Kemudian kita memiliki sub -level kedua: n = 2, ℓ = 1, dengan 3 orbital:

• N = 2, ℓ = 1, m _ℓ = -1
• N = 2, ℓ = 1, m _ℓ = 0
• N = 2, ℓ = 1, m _ℓ = +1

Tiga orbital memiliki energi yang sama tetapi orientasi spasial yang berbeda.

Jumlah kuantum putaran m_S

Saat memecahkan persamaan Schrödinger dalam tiga dimensi, angka -angka yang sudah dijelaskan muncul. Namun, dalam hidrogen struktur lebih lanjut diamati daripada angka -angka ini tidak cukup untuk dijelaskan.

Itu dapat melayani Anda: Gase Constant: Apa itu, Perhitungan dan Contoh

Oleh karena itu, pada tahun 1921 fisik lain, Wolfgang Pauli, mengusulkan keberadaan angka keempat: angka putaran m_S, yang membutuhkan nilai +½ atau -½.

Dengan nomor ini, sifat elektron yang sangat penting dijelaskan, yang merupakan putaran, Kata yang berasal dari bahasa Inggris putaran (Balikkan diri Anda). Dan putaran pada gilirannya terkait dengan sifat magnetik atom.

Salah satu cara untuk memahami putaran adalah dengan membayangkan bahwa elektron berperilaku seperti dipol magnetik kecil (magnet dengan kutub utara dan selatan), berkat rotasi di sekitar porosnya sendiri. Belokan bisa berada di arah yang sama dengan jarum jam, atau ke arah yang berlawanan.

Meskipun Pauli menyarankan keberadaan jumlah ini, hasil percobaan yang dilakukan oleh Otto Stern dan Walter Gerlach pada tahun 1922 telah mengantisipasinya.

Para ilmuwan ini berhasil membagi seberkas atom perak dengan penerapan medan magnet yang tidak seragam.

Nilai m_S Itu tidak tergantung pada n, ℓ dan m _ℓ. Secara grafis, itu diwakili oleh panah: panah ke atas menunjukkan jadwal dan satu di Antiboran.

Prinsip Pengecualian Pauli

Perilaku elektron dalam atom dirangkum dalam prinsip pengecualian Pauli, yang menyatakan bahwa dua elektron atom tidak dapat ada dalam keadaan kuantum yang sama.

Oleh karena itu, setiap elektron harus memiliki set angka kuantum yang berbeda n, ℓ, m _ℓ dan m_S.

Pentingnya angka kuantum dan prinsip ini terletak pada pemahaman sifat-sifat elemen dalam tabel periodik: elektron diatur dalam lapisan sesuai dengan N, dan kemudian dalam sub-cap menurut ℓ dan sisa angka.

Referensi

1. Alonso, m. 1971. Kuantum dan yayasan statistik. Dana Pendidikan Inter -American.
2. Bauer, w. 2011. Fisika untuk Teknik dan Ilmu Pengetahuan. Volume 1. MC Graw Hill.
3. Chang, R. 2013. Kimia. 11va. Edisi. Pendidikan MC Graw Hill.
4. Eisberg-Resnick. 1989. Fisika kuantum. Limusa - Wiley.
5. Giambattista, a. 2010. Fisika. 2nd. Ed. Bukit McGraw.
6. Rex, a. 2011. Dasar -dasar fisika. Pearson.
7. Tippens, hlm. 2011. Fisika: Konsep dan Aplikasi. Edisi ke -7. Bukit McGraw.