Angka sempurna bagaimana mengidentifikasi mereka dan contoh

A Angka yang sempurna adalah angka alami sehingga Jumlah pembaginya sama dengan angkanya. Jelas itu tidak dapat dimasukkan di antara para pembagi dengan nomor itu sendiri.

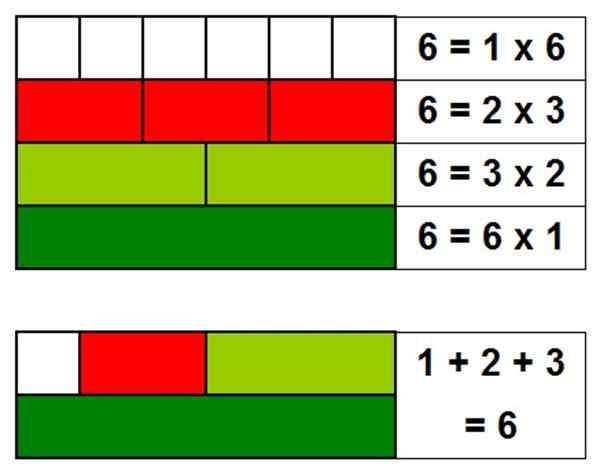
Salah satu contoh paling sederhana dari angka sempurna adalah 6, karena pembagi adalah: 1, 2 dan 3. Jika kita menambahkan pembagi, itu diperoleh: 1 + 2 + 3 = 6.

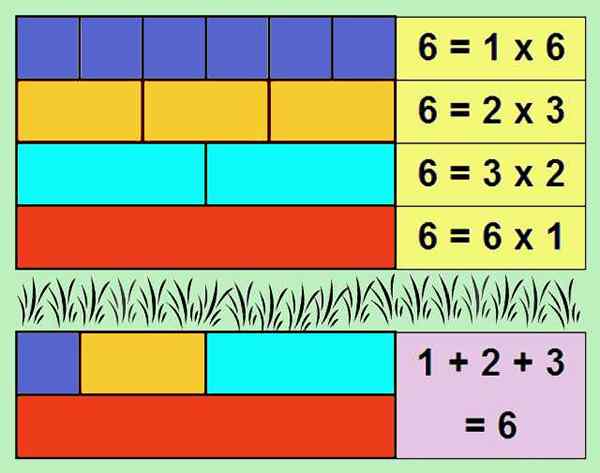Gambar 1. Angka 6 sempurna, karena jumlah pembagi, tidak termasuk angka itu sendiri, memberikan nomor 6. Sumber: Made sendiri

Jumlah para pembagi bilangan bulat, tidak termasuk angka itu sendiri, disebut alikuot. Oleh karena itu angka yang sempurna sama dengan alikuotnya.

Tetapi jika dalam jumlah pembagi dari angka angka itu sendiri termasuk, maka angka yang sempurna akan menjadi salah satu yang jumlah dari semua pembagi dibagi dengan 2 sama dengan angka itu sendiri.

[TOC]

Sejarah

Matematikawan kuno, terutama orang -orang Yunani, memberi sangat penting bagi angka yang sempurna dan mengaitkan kualitas ilahi.

Sebagai contoh, Philo de Alejandría, sekitar abad ke -1, mengklaim bahwa 6 dan 28 adalah angka sempurna yang bertepatan dengan enam hari penciptaan dunia dan dua puluh delapan hari yang dibutuhkan bulan untuk berbalik di bumi.

Angka -angka yang sempurna juga ada di alam, misalnya di kutub utara Saturnus juga muncul nomor 6 yang sempurna, pusaran berbentuk seekor segi enam yang ditemukan oleh probe Cassini dan yang telah menarik bagi para ilmuwan. 

Lebah lebah memiliki sel dalam bentuk heksagonal, yaitu dengan 6 sisi.  Ditunjukkan bahwa poligon dengan nomor 6 sempurna adalah yang memungkinkan memaksimalkan jumlah sel dalam sarang lebah, dengan lilin minimum untuk elaborasinya.

Gambar 2. Nomor 6 sempurna hadir dalam lebah sarang lebah. Ditunjukkan bahwa dengan jumlah sisi ini jumlah lilin yang akan digunakan untuk membentuk sel -sel sangat minim. Sumber: Pixabay.

Properti angka sempurna

Jumlah semua pembagi dari angka alami n dilambangkan dengan σ (n). Dalam angka yang sempurna memang benar bahwa: σ (n) = 2n.

Formula dan kriteria Euclid

Euclid menemukan formula dan kriteria yang memungkinkan Anda menemukan angka yang sempurna. Formula ini adalah:

2^(N-1) (2^N -1)

Namun, angka yang dihasilkan oleh formula akan sempurna hanya ketika faktor (2^N -1) Jadilah sepupu.

Dapat melayani Anda: komponen persegi panjang dari vektor (dengan latihan)

Mari kita lihat bagaimana angka sempurna pertama dihasilkan:

Jika n = 2 maka kami memiliki 2¹ (2² - 1) = 2 x 3 = 6 yang sudah kita lihat itu sempurna.

Saat n = 3 Anda memiliki 2² (2³ - 1) = 4 x 7 = 28 yang juga sempurna karena diverifikasi secara rinci dalam contoh 1.

Mari kita lihat apa yang terjadi dengan n = 4. Dengan mengganti dalam formula Euclid yang kami miliki:

2³ (2⁴ - 1) = 8 x 15 = 120

Dapat diverifikasi bahwa nomor ini tidak sempurna, seperti yang ditunjukkan secara rinci dalam Contoh 3. Ini tidak bertentangan dengan kriteria Euclid, karena 15 bukan sepupu, persyaratan yang diperlukan untuk hasilnya menjadi angka yang sempurna.

Mari kita lihat apa yang terjadi saat n = 5. Menerapkan formula yang kami miliki:

2⁴ (2⁵ - 1) = 16 x 31 = 496

Karena 31 adalah bilangan prima, jadi nomor 496 harus sempurna, menurut kriteria Euclid. Dalam Contoh 4 ditunjukkan secara rinci bahwa itu secara efektif.

Bilangan prima yang memiliki formulir 2^P - 1 Mereka disebut sepupu Mersenne, untuk menghormati bhikkhu Marin Mersenne, yang mempelajari bilangan prima dan angka sempurna pada abad ketujuh belas.

Selanjutnya pada abad kedelapan belas Leonhard Euler menunjukkan bahwa semua angka sempurna yang dihasilkan oleh formula Euclid adalah pasangan.

Sampai saat ini, sempurna telah ditemukan itu aneh.

Jumlah sempurna terbesar yang diketahui

Ke tanggal saat ini 51 angka sempurna diketahui, semua dihasilkan oleh rumus dan kriteria euclid. Jumlah ini diperoleh setelah sepupu Mersenne ditemukan, yaitu: (2^82589933 - 1).

Angka sempurna #51 adalah (2^82589933) X (2^82589933 - 1) dan memiliki 49724095 digito.

Angka yang sempurna adalah teman diri Anda

Dalam teori angka dikatakan bahwa dua angka adalah teman ketika jumlah pembagi satu, tidak termasuk angka itu sendiri, sama dengan angka lainnya dan sebaliknya.

Itu dapat melayani Anda: segmen garis dan semi -river

Pembaca dapat memverifikasi bahwa jumlah pembagi 220, tidak termasuk 220 adalah 284. Di sisi lain, jumlah pembagi 284, tidak termasuk 284, sama dengan 220. Oleh karena itu jumlah pasangan 220 dan 284 adalah teman.

Dari sudut pandang ini, jumlah yang sempurna adalah teman diri Anda.

Contoh Angka Sempurna

Selanjutnya, delapan angka sempurna pertama terdaftar:

6

28

496

8128

33550336

8589869056

137438691328

2305843008139952128

Latihan

Dalam latihan berikut, perlu untuk menghitung pembagi angka, dan kemudian membuat jumlah mereka dan memverifikasi apakah angka tersebut adalah angka yang sempurna atau tidak.

Oleh karena itu sebelum mengatasi latihan, kami akan meninjau konsep dan menunjukkan bagaimana mereka dihitung.

Untuk memulainya, Anda harus ingat bahwa angka -angka tersebut dapat menjadi sepupu (ketika mereka hanya dapat dibagi menjadi tepat dengan diri mereka sendiri dan 1) atau senyawa (ketika mereka dapat terurai sebagai produk bilangan prima).

Untuk nomor majemuk dan Anda punya:

N = a^N . B^M. C^P … R^k 

Di mana a, b, c ... r adalah bilangan prima dan n, m, p ... k adalah eksponen milik bilangan alami, yang dapat bernilai dari 1 dan seterusnya.

Dalam hal eksponen -eksponen ini, ada formula untuk mengetahui berapa banyak pembagi yang dimiliki angka n, meskipun tidak memberi tahu kita apa ini. Biarkan C menjadi jumlah ini, lalu:

C = (n +1) (m +1) (p +1) ... (k +1)

Dekomposisi angka n sebagai produk bilangan prima dan pengetahuan tentang berapa banyak pembagi memiliki, baik sepupu maupun non -cousin, akan membantu kita menentukan apa pembagi ini.

Setelah semua orang memiliki, kecuali yang terakhir yang tidak diperlukan dalam jumlah, itu dapat diverifikasi apakah itu adalah angka yang sempurna atau tidak.

- Latihan 1

Pastikan nomor 28 itu sempurna.

Larutan

Yang pertama adalah menguraikan angka dalam faktor utamanya.

28 | 2
14 | 2
07 | 7
01 | 1

Pembaginya adalah: 1, 2, 4, 7, 14 dan 28. Jika kita mengecualikan pada 28 jumlah yang diberikan para pembagi:

Dapat melayani Anda: setengah dari 15

1 + 2 + 4 + 7 + 14 = 3 + 4 + 7 + 14 = 7 + 7 + 14 = 14 + 14 = 28

Oleh karena itu 28 adalah angka yang sempurna.

Selain itu, jumlah semua pembagi adalah 28 + 28 sehingga aturan σ (28) = 2 x 28.

- Latihan 2

Memutuskan apakah nomor 38 sempurna atau tidak.

Larutan

Jumlahnya dipecah menjadi faktor utamanya:

39 | 3
13 | 13
01 | 1

Pembagi 39 tanpa memasukkan angka itu sendiri adalah: 1, 3 dan 13. Jumlah 1 + 3 + 13 = 4 + 13 = 17 tidak sama dengan 39, oleh karena itu 39 adalah angka yang tidak sempurna atau non-perfeksi. 

- Latihan 3

Cari tahu apakah nomor 120 sempurna atau tidak sempurna.

Larutan

Jumlahnya dipecah menjadi faktor utamanya:

120 | 2
060 | 2
 30 | 2
 15 | 3
  5 | 5
  1 | 1

Dari faktor utama, para pembagi ditemukan:

1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 40, 60 dan 120

Jika 120 sempurna saat menambahkan semua pembagi harus diperoleh 2 x 120 = 240. 

1 + 2 + 3 + 4 + 5 + 6 + 8 + 10 + 12 + 15 + 20 + 24 + 30 + 40 + 60 + 120 = 360

Hasil ini jelas berbeda dari 240, jadi disimpulkan bahwa angka 120 bukan angka yang sempurna.

- Latihan 4

Pastikan nomor 496, yang diperoleh dengan kriteria Euclid, adalah angka yang sempurna.

Larutan

Angka 496 dipecah menjadi faktor utamanya:

496 | 2
248 | 2
124 | 2
062 | 2
031 | 31
001 | 1

Maka pembagi mereka adalah:

1, 2, 4, 8, 16, 31, 62, 124, 248, 496

Sekarang semuanya ditambahkan, kecuali 496:

1 + 2 + 4 + 8 + 16 + 31 + 62 + 124 + 248 = 496

Mengkonfirmasi bahwa itu memang angka yang sempurna.

Referensi

1. Baldor, a. 1986. Hitung. Edisi dan distribusi Codex.
2. Semua tentang bilangan prima. Nomor teman. Pulih dari: perawat.org.
3. Wolfram Mathworld. Aturan Euler. Dipulihkan dari: MathWorld.Wolfram.com.
4. Wolfram Mathworld. Angka yang sempurna. Dipulihkan dari: MathWorld.Wolfram.com.
5. Wikipedia. Angka yang sempurna. Diperoleh dari: di.Wikipedia.org.
6. Wikipedia. Nomor teman. Pulih dari: is.Wikipedia.org.