Angka transenden yaitu, rumus, contoh, latihan

Itu Angka transenden Mereka adalah mereka yang tidak dapat diperoleh sebagai akibat dari persamaan polinomial. Kebalikan dari angka transenden adalah a Nomor aljabar, yang merupakan solusi dari persamaan polinomial tipe:

ke_N X^N + ke_N-1 X^N-1 +... + a₂ X² + ke₁ x + a₀ = 0

Dimana koefisiennya_N, ke_N-1,… ke₂, ke₁, ke₀ Mereka adalah bilangan rasional, disebut Koefisien polinomial. Jika angka x adalah solusi dari persamaan sebelumnya, maka angka itu tidak transenden.

Gambar 1. Dua jumlah yang sangat penting dalam sains adalah angka transenden. Sumber: Publik Domain Public.bersih.

Kami akan menganalisis beberapa angka dan melihat apakah mereka transenden atau tidak:

a) 3 tidak transenden karena merupakan solusi x - 3 = 0.

b) -2 tidak bisa transenden karena merupakan solusi x + 2 = 0.

C) ⅓ Solusi 3x - 1 = 0

d) Solusi Persamaan x² - 2x + 1 = 0 adalah √2 -1, jadi angka tersebut menurut definisi tidak transenden.

e) juga √2 karena itu adalah hasil dari persamaan x² - 2 = 0. Dengan menaikkan √2 persegi itu menghasilkan 2, yang dikurangi dari 2 tidak penting menjadi nol. Jadi √2 adalah bilangan irasional tetapi tidak transenden.

[TOC]

Apa angka transenden?

Masalahnya adalah tidak ada aturan umum untuk mendapatkannya (nanti kita akan mengatakan formulir), tetapi beberapa yang paling terkenal adalah nomornya pi dan Nomor Neper, dilambangkan masing -masing oleh: π Dan Dan.

Angka π

Nomor π Secara alami tampak mengamati bahwa kecenderungan matematika antara perimeter p lingkaran dan diameternya D, terlepas dari apakah itu lingkaran kecil atau besar, selalu memberikan angka yang sama, disebut pi:

π = P/D ≈ 3.14159…

Ini berarti bahwa jika diameter lingkar diambil sebagai satuan pengukuran, untuk semuanya, baik besar atau kecil, perimeter akan selalu bernilai P = 3.14… = π, seperti yang dapat dilihat dalam animasi Gambar 2.

Dapat melayani Anda: Teorema Bolzano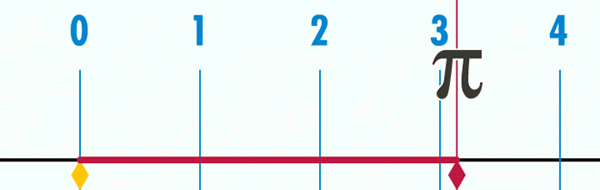Gambar 2. Panjang perimeter lingkaran kadang -kadang panjang diameter, sekitar 3,1416.

Untuk menentukan lebih banyak desimal, Anda harus mengukur lebih presisi P dan D dan kemudian menghitung hasil bagi, yang telah dilakukan dengan cara matematika. Kesimpulannya adalah bahwa desimal dari hasil bagi tidak ada habisnya dan tidak pernah diulang, jadi angkanya π Selain transenden, itu juga irasional.

Bilangan irasional adalah angka yang tidak dapat dinyatakan sebagai pembagian dua bilangan bulat. 

Diketahui bahwa setiap angka transenden tidak rasional, tetapi tidak benar bahwa semua irasional transenden. Misalnya √2 adalah irasional, tetapi tidak transenden.

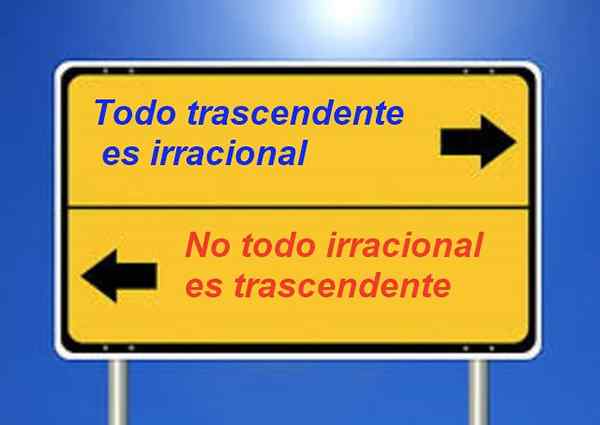Gambar 3. Angka transenden tidak rasional, tetapi pernyataan timbal balik tidak benar.

Nomor e

Jumlah transenden adalah dasar dari logaritma Neperian dan pendekatan desimal mereka adalah:

E ≈ 2.718281828459045235360… .

Jika Anda ingin menulis nomornya Dan Tepatnya, perlu untuk menulis desimal tak terbatas, karena setiap angka transenden tidak rasional, seperti yang dikatakan sebelumnya.

Sepuluh digit pertama Dan Mereka mudah diingat:

2.7 1828 1828 dan meskipun tampaknya mengikuti pola berulang, ini tidak dicapai dalam desimal urutan yang lebih besar dari sembilan.

Definisi yang lebih formal Dan adalah yang berikutnya:

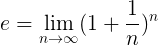
Yang berarti bahwa nilai yang tepat dari Dan Operasi yang ditunjukkan dalam formula ini tercapai, saat angka alami N Itu cenderung tak terbatas.

Ini menjelaskan mengapa kita hanya bisa mendapatkan pendekatan Dan, Karena betapapun besar angka N ditempatkan, Anda selalu dapat menemukan a N tua.

Mari kita cari beberapa pendekatan sendiri:

-Saat n = 100 lalu (1 + 1/100)¹⁰⁰ = 2.70481 yang nyaris tidak bertepatan dalam desimal pertama dengan nilai "benar" dari E.

-Jika Anda dipilih n = 10.000 yang Anda miliki (1 + 1/10.000)^10.000 = 2.71815 yang bertepatan dengan nilai E "tepat" dalam tiga desimal pertama.

Dapat melayani Anda: sisi homolog

Proses ini harus diikuti untuk dapat memperoleh nilai "benar" dari E. Saya tidak berpikir kita punya waktu untuk mencapainya, tapi mari kita lakukan satu upaya lagi:

Mari kita gunakan n = 100.000:

(1 + 1/100.000)^100.000 = 2.7182682372

Bahwa ia hanya memiliki empat desimal yang bertepatan dengan nilai yang dianggap akurat.

Yang penting adalah memahami bahwa semakin besar nilai N yang dipilih untuk menghitung dan_N, Lebih dekat akan menjadi nilai sebenarnya. Tetapi nilai sebenarnya hanya akan dipegang ketika n tidak terbatas.

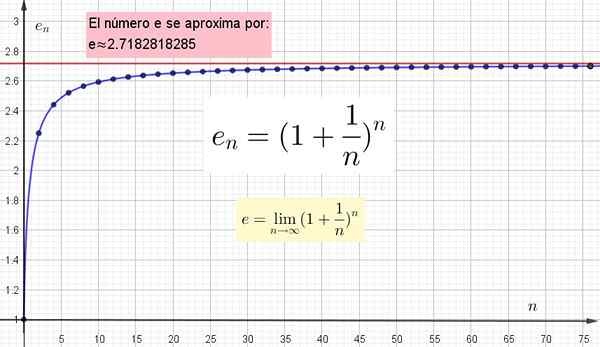Gambar 4. Secara grafis ditampilkan sebagai nilai n yang lebih tinggi lebih dekat ke E, tetapi untuk mencapai nilai yang tepat n harus tak terbatas.

Angka transenden lainnya

Terlepas dari angka -angka terkenal ini ada angka transenden lainnya, misalnya:

- 2^√2

Angka aljabar apa pun, yang bukan 0 atau 1, diangkat ke eksponen irasional akan menjadi angka transenden.

-Nomor 10 Champernowne: 

C_10 = 0.123456789101112131415161718192021… .

-Nomor Champernowne di pangkalan 2:

C_2 = 0.110111001011011… .

-Γ atau gamma konstan Euler-Mascheroni:

γ ≈ 0,577 215 664 901 532 860 606

Yang diperoleh dengan melakukan perhitungan berikut:

γ ≈ 1 + ½ + ⅓ + ¼ + ... + 1/n - ln (n)

Kapan N menjadi sangat besar. Untuk memiliki nilai yang tepat dari nomor gamma yang perlu dihitung N tak terbatas. Sesuatu yang mirip dengan apa yang kami lakukan di atas.

Dan ada lebih banyak angka transenden. Matematikawan agung Georg Cantor, lahir di Rusia dan hidup antara tahun 1845 dan 1918, menunjukkan bahwa himpunan angka transenden jauh lebih besar daripada himpunan bilangan aljabar.

Rumus di mana angka transenden π muncul

Perimeter keliling

P = π d = 2 π r, di mana p adalah perimeter, d diameter dan r jari -jari keliling. Harus diingat bahwa:

Dapat melayani Anda: berapa banyak yang harus Anda tambahkan ke 3/4 untuk mendapatkan 6/7?

-Diameter keliling adalah segmen terpanjang yang bergabung dengan dua titik dan yang selalu melewati pusatnya,

-Jari -jari adalah setengah dari diameter dan merupakan segmen yang bergerak dari tengah ke tepi.

Area lingkaran

A = π r² = ¼ π D²

Permukaan bola

S = 4 π r^2.

Ya. Meskipun sepertinya tidak, permukaan bola sama dengan empat lingkaran dengan jari -jari yang sama dengan bola.

Volume bola

V = 4/3 π r³

Latihan

- Latihan 1

Pizzeria "eksotis" menjual tiga pizza berdiameter: 30 cm kecil, median 37 cm dan besar 45 cm. Seorang anak sangat lapar dan menyadari bahwa dua pizza kecil memiliki biaya yang sama dengan yang besar. Apa yang akan lebih baik baginya, beli dua pizza kecil atau besar?

Gambar 5.- Area pizza sebanding dengan kuadrat jari -jari, menjadi konstanta proporsionalitas. Sumber: Pixabay.

Larutan

Semakin besar area, semakin besar jumlah pizza, karena alasan ini area pizza besar akan dihitung dan dibandingkan dengan dua pizza kecil:

Area pizza besar = ¼ π D² = ¼ ⋅3.1416⋅45² = 1590.44 cm²

Area pizza kecil = ¼ π D² = ¼ ⋅3.1416⋅30² = 706.86 cm²

Oleh karena itu dua pizza kecil akan memiliki area 

2 x 706.86 = 1413.72 cm² .

Jelas: akan ada lebih banyak pizza membeli satu besar dari dua anak kecil.

- Latihan 2

Pizzeria "Exotic" juga menjual semi -man -pizza radius 30 cm untuk bentuk persegi panjang yang sama dengan sisi 30 x 40 cm. Mana yang akan Anda pilih?

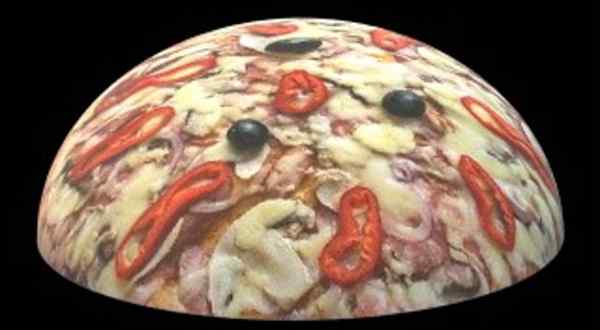Gambar 6.- Permukaan semi -speaker adalah dua kali permukaan melingkar dasar. Sumber: f. Zapata.

Larutan

Seperti yang dinyatakan pada bagian sebelumnya, permukaan bola empat kali lebih besar dari lingkaran dengan diameter yang sama, sehingga semi -spear berdiameter 30 cm akan memiliki:

30 cm semi -man -pizza: 1413.72 cm² (dua kali melingkar dengan diameter yang sama)

Pizza persegi panjang: (30 cm) x (40 cm) = 1200 cm² .

Semi -Man -Pizza memiliki area yang lebih besar.

Referensi

1. Fernández J. Nomor e. Asal dan keingintahuan. Pulih dari: matematika kedelai.com
2. Nikmati matematika. Nomor Euler. Pulih dari: nikmatiMaticaticas.com.
3. Figuera, J. 2000. Matematika 1. Diversifikasi. Edisi Co-Bo.
4. Garcia, m. Angka E dalam perhitungan dasar. Pulih dari: matematika.Ciens.UCV.pergi.
5. Wikipedia. Nomor pi. Pulih dari: wikipedia.com
6. Wikipedia. Angka transenden. Pulih dari: wikipedia.com