Rumus gelombang stasioner, karakteristik, jenis, contoh

Itu Gelombang berdiri Mereka adalah gelombang yang menyebar di setengah terbatas, pergi dan datang di bagian ruang, tidak seperti gelombang perjalanan, yang ketika menyebarkan pindah dari sumber yang berasal dan tidak kembali ke sana.

Mereka adalah dasar dari suara yang diproduksi dalam alat musik, karena mereka muncul dengan mudah pada senar tetap, baik di salah satu ujungnya atau keduanya. Mereka juga dibuat dalam membran tegang seperti drum atau tabung di dalam dan struktur seperti jembatan dan bangunan.

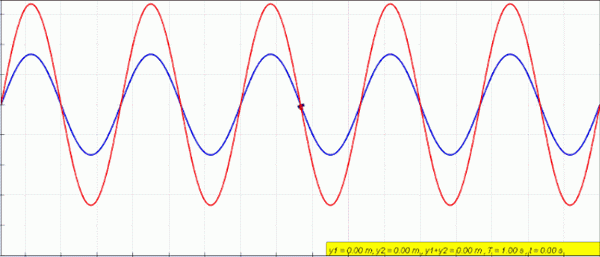Animasi gelombang stasioner (merah) yang dibuat oleh superposisi gelombang kiri (biru) dan kanan (hijau). Sumber: Lookangmany Terima kasih kepada penulis simulasi asli = Wolfgang Christian dan Francisco Schembre penulis simulasi java mudah = Francisco Schembre/CC BY-SA (https: // createvecommons.Org/lisensi/by-sa/4.0)

Ketika Anda memiliki tali tetap di kedua ujungnya, seperti gitar, misalnya, gelombang dibuat dengan amplitudo dan frekuensi yang identik, yang bergerak dalam indera yang berlawanan dan menggabungkan menghasilkan fenomena yang disebut gangguan.

Jika gelombang berada dalam fase, punggung dan lembah disejajarkan dan menghasilkan gelombang dengan amplitudo ganda. Dalam hal ini ada pembicaraan tentang gangguan konstruktif.

Tetapi jika gelombang yang mengganggu berada di luar fase, punggung satu memenuhi lembah orang lain dan amplitudo yang hasilnya adalah nol. Itu kemudian merupakan gangguan yang merusak.

[TOC]

Rumus dan Persamaan

Elemen utama gelombang untuk mewakilinya dalam ruang dan waktu adalah amplitudo A, panjang gelombangnya λ dan frekuensi sudutnya Ω.

Elemen gelombang. Sumber: Wikimedia Commons.

Dalam representasi matematika lebih disukai menggunakan k, daripada Nomor Gelombang o Jumlah kali gelombang per unit sedang terjadi. Itulah sebabnya didefinisikan melalui panjang gelombang λ yang merupakan jarak antara dua lembah atau dua punggung:

K = 2π/ λ

Selagi frekuensi sudut Ini terkait dengan periode atau durasi osilasi lengkap, seperti:

Ω = 2π/ t

Dan juga frekuensi F diberikan oleh:

F = Ω / 2π

Karena itu:

F = 1/t

Selain itu, gelombang bergerak dengan kecepatan v berdasarkan:

V = λ.F

Ekspresi matematika dari gelombang stasioner

Secara matematis kita dapat mengekspresikan gelombang melalui fungsi sinus atau fungsi kosinus. Misalkan ada gelombang dengan amplitudo yang sama A, panjang gelombang λ dan frekuensi Ω, menyebar di sepanjang tali dan dalam arti yang berlawanan:

Dan₁ = Dosa (kx - ωt)

Dan₂ = Dosa (kx + ωt)

Saat menambahkannya, kami menemukan gelombang yang dihasilkan dan_R:

Dan_R = y₁ + Dan₂ = Sen (kx - ωt) + dosa (kx + ωt)

Ada identitas trigonometri untuk menemukan jumlahnya:

Dapat melayani Anda: apa itu kekasaran relatif dan absolut?

sin α + sin β = 2 sin (α + β)/2 . cos (α - β)/2

Melalui identitas ini, gelombang yang dihasilkan dan_R tersisa:

Dan_R = [2a sen kx] . cos ωt

Lokasi node dan perut

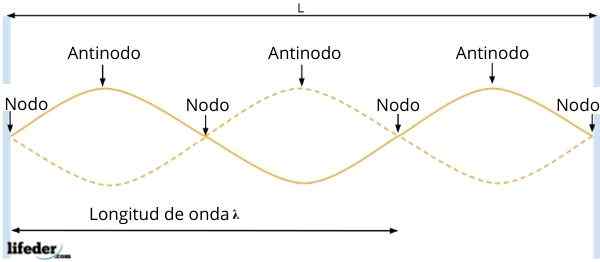Antinodos atau perut dan node

Gelombang yang dihasilkan memiliki amplitudo_R = 2ase kx, yang tergantung pada posisi partikel. Kemudian, pada titik -titik di mana sen kx = 0, amplitudo gelombang dibatalkan, yaitu, tidak ada getaran.

Poin -poin ini adalah:

Kx = π, 2π, 3π ..

Sebagai k = 2 π/ λ:

(2 π/ λ) x = π, 2π, 3π ..

x = λ/2, λ, 3λ/2 ..

Dalam titik -titik seperti itu gangguan destruktif terjadi dan mereka dipanggil node. Mereka dipisahkan oleh jarak yang sama dengan λ/2, sebagaimana disimpulkan dari hasil sebelumnya.

Dan antara dua node berturut -turut adalah antinodos atau perut, di mana amplitudo gelombang maksimum, karena gangguan konstruktif terjadi. Mereka terjadi ketika:

sin kx = ± 1

Kx = ± π/2, 3π/2, 5π/2 ..

Sekali lagi k = 2 π/ λ dan kemudian:

x = λ /4, 3λ /4, 5λ /4, ..

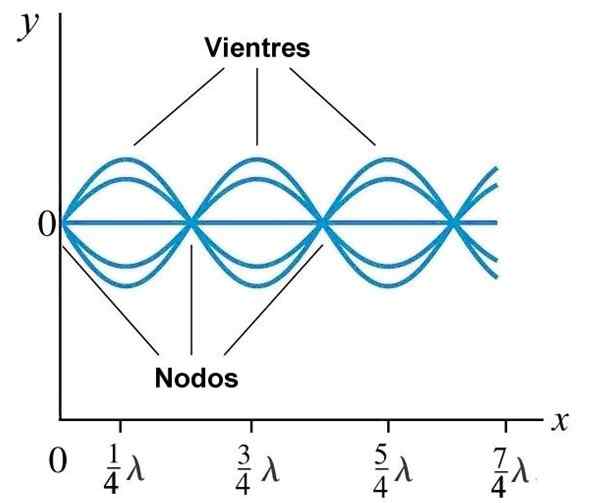Perut atau antinode dan node dalam gelombang stasioner yang dihasilkan pada tali dengan ujung tetap pada x = 0. Sumber: Wikimedia Commons.

Mode normal pada tali

Kondisi perbatasan pada tali menentukan bagaimana panjang gelombang dan frekuensi. Jika tali panjang L difiksasi oleh dua ujungnya, ia tidak dapat bergetar dengan frekuensi apa pun, karena titik -titik di mana tali tetap sudah ada node.

Selain itu, pemisahan antara node yang berdekatan adalah λ/2, dan antara simpul dan perut adalah λ/4, dengan cara ini hanya untuk panjang gelombang tertentu dihasilkan gelombang stasioner: yang di mana integer λ/2 di dalam disesuaikan dari itu:

(λ/2) = l, dengan n = 1, 2, 3, 4 .. .

Karena itu:

λ = 2l/n

Harmonik

Nilai yang berbeda yang diambil λ disebut Harmonik. Demikianlah kita memiliki:

-Harmonik Pertama: λ = 2L

-Harmonik Kedua: λ = l

-Harmonik Ketiga: λ = 2 l/3

-Ruang Harmonik: λ = l/2

Dan seterusnya.

Kecepatan dan frekuensi

Meskipun gelombang stasioner tampaknya tidak bergerak, persamaannya masih valid:

V = λ. F

Karena itu:

v = (2l/n) . F

F = nv/2l

Sekarang, dapat ditunjukkan bahwa kecepatan gelombang bergerak dalam tali tergantung pada tegangan T dalam hal yang sama dan kepadatan linier massa μ (massa per satuan panjang) sebagai:

Karena itu:

Dapat melayani Anda: beban mati: karakteristik, perhitungan, contoh

Fitur gelombang stasioner

-Saat gelombang diam, gelombang yang dihasilkan tidak menyebar seperti komponennya, yang beralih dari satu tempat ke tempat lain. Ada titik di mana y = 0 karena tidak ada getaran: node, dengan kata lain, amplitudo untuk_R Itu nol.

-Ekspresi matematika dari gelombang stasioner terdiri dari produk bagian spasial (yang tergantung pada koordinat x atau koordinat ruang) dan bagian temporal.

-Di antara node, gelombang hitam yang dihasilkan berosilasi di satu tempat, sedangkan gelombang yang berpindah dari satu tempat ke tempat lain sudah ketinggalan zaman di sana.

-Hanya di node, energi tidak diangkut, karena ini sebanding dengan kuadrat amplitudo, tetapi terperangkap di antara node.

-Jarak antara node yang berdekatan adalah setengah dari panjang gelombang.

-Poin di mana tali ditetapkan juga dianggap node.

Teman-teman

Gelombang stasioner dalam dimensi

Gelombang dalam tali tetap adalah contoh gelombang stasioner dalam dimensinya, yang deskripsi matematika yang kami tawarkan di bagian sebelumnya.

Gelombang stasioner dalam dua dan tiga dimensi

Gelombang stasioner juga dapat disajikan dalam dua dimensi, menjadi deskripsi matematika yang sedikit lebih kompleks.

Balap contoh ondas

Tetap string

-String yang dipasang oleh ekstrem yang terosilasi dengan tangan atau dengan satu piston oleh yang lain menghasilkan gelombang stasioner sepanjang panjangnya.

Alat-alat musik

Gelombang stasioner dibuat dalam alat musik seperti Violoncello. Sumber: Pixabay.

-Saat memainkan instrumen string seperti gitar, harpa, biola dan piano.

Gelombang Stlover juga dibuat dalam tabung udara, seperti tabung organ.

Bangunan dan jembatan

Gelombang stasioner muncul dalam struktur seperti jembatan dan bangunan. Kasus yang luar biasa adalah kasus Tacoma Narrows Suspension di dekat kota Seattle, Amerika Serikat. Tak lama setelah diresmikan pada tahun 1940, jembatan ini runtuh karena gelombang stasioner yang dibuat di dalam angin.

Frekuensi angin cocok dengan frekuensi alami jembatan, menciptakan gelombang stasioner dalam hal ini, yang meningkatkan amplitudo mereka sampai jembatan runtuh. Fenomena ini dikenal sebagai resonansi.

Itu bisa melayani Anda: refleksi cahaya

Seiches

Di pelabuhan ada fenomena yang sangat aneh yang disebut Seiche, di mana gelombang laut menghasilkan osilasi besar. Ini karena air di pelabuhan cukup tertutup, meskipun air samudera sering menembus pintu masuk pelabuhan.

Port Waters bergerak dengan frekuensi mereka sendiri, dan juga lautan. Jika kedua air cocok dengan frekuensi mereka, ada gelombang stasioner besar karena resonansi, seperti yang terjadi dengan Jembatan Tacoma.

Itu Seiches Mereka juga dapat terjadi di danau, waduk, kolam renang dan badan air lainnya dibatasi oleh permukaan.

Tangki ikan

Gelombang stasioner dapat dibuat dalam fishbowl yang diangkut oleh seseorang, jika frekuensi orang tersebut sama dengan frekuensi ayunan air.

Olahraga diselesaikan

Tali gitar memiliki l = 0.9 m dan kepadatan adonan linier μ = 0.005 kg/m. Ini mengalami tegangan 72 N dan mode getarannya adalah yang menunjukkan gambar, dengan amplitudo 2a = 0.5 cm.

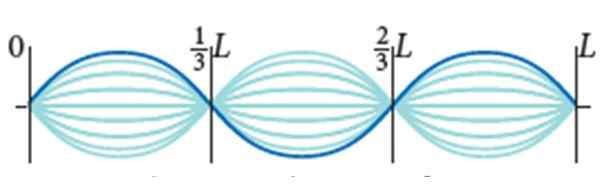Gelombang stasioner di tali gitar. Sumber: Bauer, W. Fisik.

Menemukan:

a) kecepatan propagasi

b) frekuensi gelombang

c) persamaan gelombang stasioner yang sesuai.

Solusi untuk

Melalui:

Diperoleh;

V = [72 N/(0.005 kg/m)]^1/2  = 120 m/s.

Solusi b

Jarak antara dua node yang berdekatan adalah λ/2, oleh karena itu:

(2/3) l - (1/3) l = λ/2

(1/3) l = λ/2

λ = 2l/3 = 2 x 0.90 m / 3 = 0.60 m.

Seperti v = λ.F

F = (120 m/ s)/ 0.60 m = 200 detik^-1= 200 Hz.

Solusi c

Persamaannya adalah:

Dan_R = [2a sen kx] . cos ωt

Kita perlu mengganti nilai:

K = 2π/ λ = k = 2π/ 0.60 m = 10 π/3

F = Ω / 2π

Ω = 2π x 200 Hz = 400 π Hz.

Amplitudo 2A sudah diberikan oleh pernyataan:

2a = 0.5 cm = 5 x 10 ^-3 M.

Karena itu:

Dan_R = 5 x 10 ^-3 M . sin [(10π/3) x] . cos (400πt) =

= 0.5 cm . sin [(10π/3) x] . cos (400πt)

Referensi

1. Bauer, w. 2011. Fisika untuk Teknik dan Ilmu Pengetahuan. Volume 1. MC Graw Hill.
2. Figueroa, d. (2005). Seri: Fisika untuk Sains dan Teknik. Volume 7. Gelombang dan fisika kuantum. Diedit oleh Douglas Figueroa (USB).
3. Giancoli, d.  2006. Fisika: Prinsip dengan aplikasi. 6. Ed Prentice Hall.
4. Serway, r., Jewett, J. (2008). Fisika untuk Sains dan Teknik. Volume 1. 7. Ed. Pembelajaran Cengage.
5. Tipler, hlm. (2006) Fisika untuk Sains dan Teknologi. Edisi ke -5. Volume 1. Editorial dikembalikan.
6. Wikipedia. Seiche. Pulih dari: is.Wikipedia.org.