Elemen pentadecágono, klasifikasi, karakteristik, olahraga

A Pentadecantagon Itu adalah sosok datar yang dibangun dengan lima belas segmen lurus dan tertutup. Angka semacam ini disebut poligon dan mereka dinamai sesuai dengan jumlah sisi yang memiliki.

Segitiga, dengan tiga sisi dan segi empat, dari empat, adalah contoh poligon yang sangat akrab, tetapi poligon mungkin memiliki lebih banyak sisi.

Gambar 1.  Pentagon biasa dengan simpul merah. Sumber: Wikimedia Commons.

Elemen dasar pentadecágono sama dengan poligon apa pun, terlepas dari jumlah sisi yang dimilikinya. Elemen -elemen ini adalah:

-Sisi, yang merupakan segmen yang membentuk pentadecágono dengan total 15.

-Sudut, juga 15, yang merupakan ujung sisi yang berdekatan.

-Sudut internal, Yang terbentuk di dalam pentadecágono antara dua sisi yang berdekatan.

-Sudut eksternal, terbentuk antara satu sisi dan perpanjangan salah satu sisi berturut -turut.

-Diagonal, Segmen garis yang bergabung dengan dua simpul yang tidak adil.

[TOC]

Klasifikasi

Pentadecágono bisa reguler salah satu tidak teratur, tergantung pada ukuran sisi mereka dan ukuran sudut internalnya. Jika Anda memiliki semua sisi dan sudut internal yang sama -quilátero dan equiook - itu teratur, seperti yang ditunjukkan pada Gambar 1, jika tidak itu tidak teratur.

Itu juga dapat diklasifikasikan sebagai cembung salah satu cekung. Pentagon cekung memiliki satu atau lebih sudut internal lebih besar dari 180º, sedangkan satu selalu cembung memiliki sudut internal kurang dari 180º. Pentagon biasa adalah cembung.

Kriteria klasifikasi lain dipertimbangkan jika pihaknya yang tidak berurutan - atau ekstensi mereka - dipotong atau tidak. Ketika mereka tidak dipotong, seperti dalam kasus Gambar 1, dikatakan bahwa itu adalah pentadecágon sederhana. Dan jika dipotong, maka itu rumit.

Itu dapat melayani Anda: geometri analitik

Pentagon biasa

Pentagon biasa, yang sisi dan sudut internalnya memiliki ukuran yang sama, adalah sosok simetri yang hebat, karena elemen tambahan berikut didefinisikan kepada yang dijelaskan sebelumnya:

-Tengah: Titik yang menjadi equidista dari simpul dan sisi.

-Radio: Jarak dari tengah ke salah satu simpul Pentagon biasa.

-Sudut tengah: Orang yang memiliki simpulnya di tengah sosok dan sisi -sisinya melewati dua simpul yang berdekatan.

-Apothem, Itu adalah segmen tegak lurus yang bergabung dengan pusat satu sisi dengan pusat sosok.

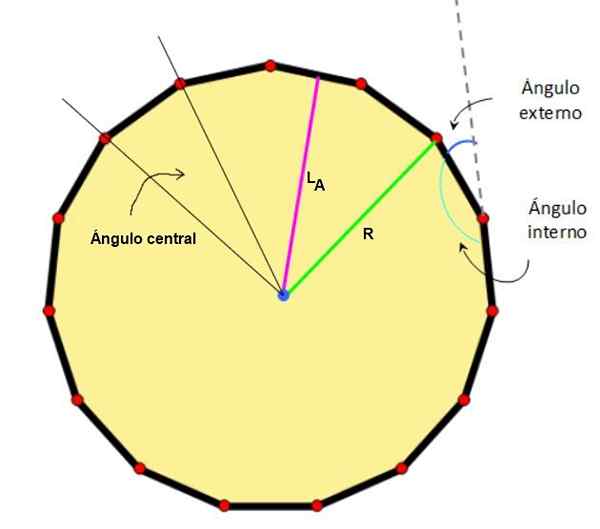Gambar 2. Tengah, apothem, radio, dan sudut penting dari pentadecágono. Sumber: Wikimedia Commons/F. Zapata.

- Karakteristik Pentagon biasa

Sudut internal

Formula berikut digunakan untuk menghitung ukuran I dari sudut internal poligon biasa, di mana N Itu adalah jumlah sisi:

Dalam rumus ini, ukuran I hadir dalam derajat, untuk mengekspresikannya dalam Radianes, dikalikan dengan faktor π/180. Mari kita lihat apa ukuran sudut internal Pentagon biasa, mengganti n = 15:

I = [(15-2) × 180º]/15 = 156º

Setara dengan radian 13π/15. Karena sudut internal pentagon biasa kurang dari 180º, itu adalah poligon cembung.

Jumlah sudut internal

Dimungkinkan untuk menghitung jumlah sudut internal dengan formula berikut:

S = (n-2) x 180º

Seperti biasa, N mewakili jumlah sisi. Rumus ini berlaku untuk n = 3, 4, 5 .. .

Melakukan n = 15 kita mendapatkan:

S = (15 - 2) x 180º = 2340º

Sudut eksternal

Sudut internal dan sudut eksternal adalah pelengkap, yaitu jumlahnya adalah 180º, sebagaimana dicatat pada Gambar 2. Oleh karena itu sudut eksternal dari Pentadecágono mengukur:

Dapat melayani Anda: binomial terkonjugasi: bagaimana itu diselesaikan, contoh, latihan

180 º - 156º = 24º.

Perimeter dan Area

Perimeter adalah ukuran kontur poligon dan dengan mudah menambahkan semua sisi. Ya ke Itu adalah panjang sisi, cukup untuk berlipat ganda N, Jumlah sisi.

Untuk pentagon biasa dari sisi A, perimeter P adalah:

P = 15a

Jika itu adalah sosok yang tidak teratur, di mana ukuran sisi berbeda, perimeter menambah panjang semua sisinya.

Adapun daerah tersebut, kami dapat menghitungnya dalam beberapa cara. Misalnya kami memiliki formula yang memungkinkan Anda untuk mendapatkannya mengetahui panjang sisi:

Melakukan operasi yang ditunjukkan, masih sekitar:

A = 17.6426⋅a²

Ada opsi lain, berlaku untuk poligon biasa. Ini tentang membaginya menjadi segitiga dasar yang sama dengan poligon. Ketinggian segitiga adalah panjang apothem l_KE, didefinisikan di atas.

Area segitiga tersebut dihitung dengan rumus yang diketahui dengan baik: basis x tinggi /2. Dengan cara ini area segitiga tunggal adalah:

Area = a. L_KE /2

Untuk memiliki luas total poligon, itu cukup untuk berlipat ganda dengan jumlah sisi n, yang dalam hal ini adalah 15:

A = 15⋅a⋅ l_KE /2

Dan karena perimeter gambar adalah p = 15⋅a, lalu:

A = p⋅ l_KE /2

Diagonal

Diagonal adalah segmen yang menyatukan dua simpul non -berturut -turut, seperti yang dinyatakan di atas. Untuk mengetahui berapa banyak diagonal yang dimiliki poligon biasa N Sisi, termasuk pentadecágono, ada formula berikut:

Dimana d adalah jumlah diagonal.

Sekarang kami mengganti n = 15, untuk mendapatkan diagonal total:

Dapat melayani Anda: poligon biasa: sifat, elemen, sudut, contoh

D = [15 × (15-3)]/2 = 90 Diagonals.

Konstruksi dengan aturan dan kompas

Pentadecágono dibangun dengan aturan dan kompas mulai dari lingkar. 360º harus dibagi menjadi 15 bagian yang sama dari 24º masing -masing. Pertama, konstruksi tambahan yang ditunjukkan dalam animasi dilakukan untuk mendapatkan sudut 60º, yang dibagi pada gilirannya menjadi 36º dan 24º.

Gambar 3. Konstruksi dengan aturan dan kompas pentagon biasa. Sumber: Wikimedia Commons.

Olahraga diselesaikan

Jika perimeter pentadecágono terdaftar dalam lingkaran jari -jari R adalah 12,56 cm. Menghitung:

A) Radio.

b) daerah Anda.

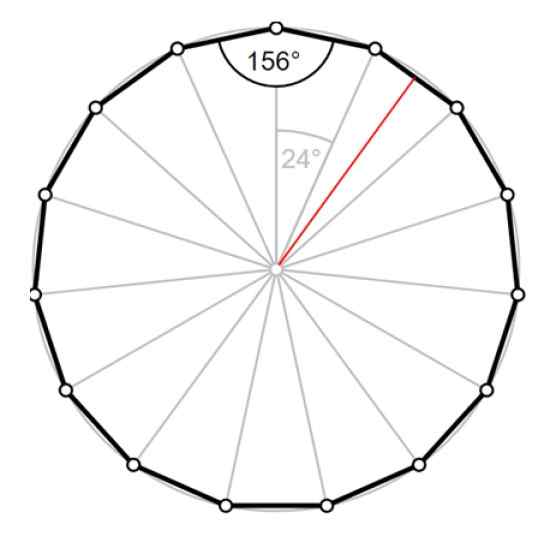Gambar 4. Pentadecágono: sudut tengah, sudut internal dan apothema merah. Sumber: Wikimedia Commons/F. Zapata.

Solusi untuk

Perimeter adalah P = 15⋅a = 12.56 cm, oleh karena itu sisi dari pentadecágono adalah 0.8373 cm. Radio Kita dapat menghitungnya dengan bantuan salah satu segitiga pada Gambar 4.

Apothem l_KE sesuai dengan ketinggian segitiga, digambar merah, yang membagi sudut 24º menjadi dua sudut masing -masing 12º.

Ada dua segitiga kanan dengan sudut internal masing -masing 12º, dan untuk salah satu dari mereka kita dapat menerapkan trigonometri untuk menemukan hipotenus, yang merupakan panjang R jari -jari.

Cara ini:

sen 12º = (a /2) /r

R = (a /2) /sen 12º = (0.8373 cm / 2) / sen12º = 2.01 cm.

Solusi b

Kita dapat menghitung area pentadecágono menggunakan rumus:

A = p⋅ l_KE /2

Kita sudah tahu perimeter p = 12.56 cm, dan panjang apothem dihitung dengan garis singgung atau cosinus 12º:

Cos 12º = l_KE / R

L_KE = R. cos 12 º = 2.01 cm. cos 12 º = 1.97 cm

Mengganti:

A = 12.56 cm⋅ 1.97 cm /2 = 12.35 cm²

Referensi

1. Alexander, d. 2013. Geometri. Ke -5. Edisi. Pembelajaran Cengage.
2. Belajar matematika. Angka geometris. Pulih dari: rodrigoanchorena.Wixsite.com.
3. Matematika Sangaku. Elemen poligon dan klasifikasinya. Pulih dari: sangakoo.com.
4. Wikipedia. Pentadecágono. Pulih dari: is.Wikipedia.org.
5. Dunia Matematika Wolfram. Pentadecagon. Dipulihkan dari: MathWorld.Wolfram.com.