Formula Prinsip Archimedes, Demonstrasi, Aplikasi

Dia Prinsip Archimedes Dia mengatakan bahwa tubuh yang benar -benar atau sebagian terendam menerima kekuatan vertikal yang disebut dorongan, yang setara dengan berat volume cairan yang dipindahkan oleh tubuh. 

Beberapa benda mengapung di dalam air, yang lain tenggelam dan sebagian membenamkan diri mereka sendiri. Untuk menenggelamkan bola pantai, perlu melakukan upaya, karena kekuatan itu segera dianggap yang mencoba mengembalikannya ke permukaan. Sebaliknya, bola logam dengan cepat tenggelam. 

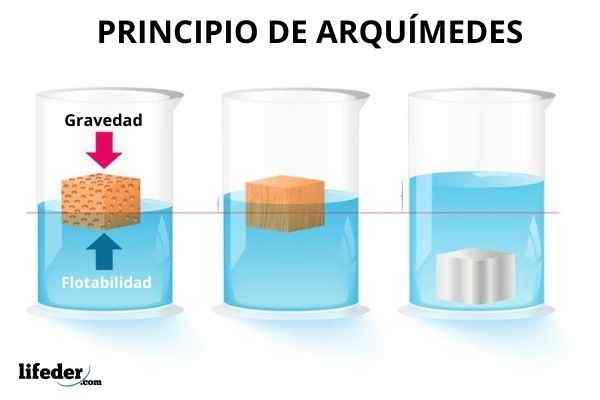
Di sisi lain, benda yang terendam tampak lebih ringan, oleh karena itu ada kekuatan yang diberikan oleh cairan yang bertentangan dengan berat badan. Tetapi Anda tidak selalu bisa memberi kompensasi sama sekali untuk gravitasi. Dan, meskipun lebih jelas dengan air, gas juga mampu menghasilkan kekuatan ini pada benda yang direndam di dalamnya.

[TOC]

Sejarah

Archimedes of Syracuse (287-212 a. C.) Itu adalah orang yang pasti menemukan prinsip ini, menjadi salah satu ilmuwan terhebat dalam sejarah. Mereka mengatakan bahwa Raja Hierón II dari Syracuse mengirim seorang tukang emas untuk memproduksi mahkota baru, yang dia berikan kepadanya sejumlah emas.

Archimedes

Ketika raja menerima mahkota baru, dia memiliki berat yang tepat, tetapi dia curiga bahwa tukang emas telah menipu dia dengan menambahkan perak, bukan emas. Bagaimana saya bisa memeriksanya tanpa menghancurkan mahkota?

Hierón disebut Archimedes, yang ketenaran sarjana terkenal, untuk membantunya menyelesaikan masalah. Legenda itu menegaskan bahwa Archimedes tenggelam di bak mandi ketika dia menemukan jawabannya dan, seperti itu emosinya, sehingga dia berlari telanjang di jalan -jalan Syracuse untuk mencari raja yang berteriak "Eureka", yang berarti "aku menemukannya".

https: // giphy.com/gifs/stito3echtlnbvliz3

Apa yang ditemukan Archimedes? Nah, saat mengambil kamar mandi permukaan air di bak mandi, saat ia masuk, yang berarti bahwa tubuh yang terendam menggantikan volume cairan tertentu.

Dan jika saya merendam mahkota dalam air, itu juga harus memindahkan volume air tertentu jika mahkota terbuat dari emas dan yang berbeda jika terbuat dari paduan dengan perak.

Formula Prinsip Archimedes

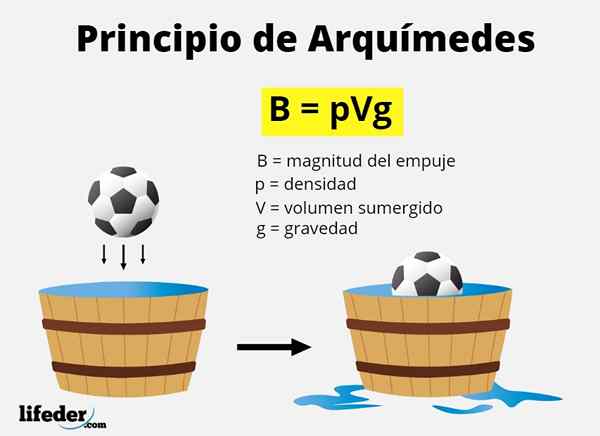
Kekuatan promosi yang dimaksud dalam prinsip Archimedes dikenal sebagai dorongan hidrostatik salah satu kekuatan pengapungan Dan, seperti yang telah kami katakan, itu setara dengan berat volume cairan yang digantikan oleh tubuh saat tenggelam.

Volume yang dipindahkan setara dengan volume objek yang terendam, baik sepenuhnya maupun sebagian. Karena beratnya apapun mg, Dan massa cairannya Kepadatan x volume, Menyangkal bagaimana B ke besarnya dorongan, secara matematis harus:

B = m_fasih x g = kerapatan cairan x gravitasi volume x terendam

B = ρ_fasih x v_terendam x g

Di mana huruf Yunani ρ ("rho") menunjukkan kepadatan.

Berat yang jelas

Berat objek dihitung dengan ekspresi yang diketahui dengan baik mg, Namun, hal -hal terasa lebih ringan saat terendam di dalam air. 

Dia Berat yang jelas Dari suatu objek adalah apa yang dimiliki ketika direndam dalam air atau cairan lainnya dan mengetahuinya, Anda dapat memperoleh volume objek yang tidak teratur seperti mahkota raja hierón, seperti yang akan dilihat di bawah ini.

Dapat melayani Anda: 13 contoh hukum pertama Newton dalam kehidupan nyata

Untuk melakukan ini, itu benar -benar terendam dalam air dan tunduk pada tali yang melekat pada a dinamo meter -instrumen yang dilengkapi dengan pegas yang berfungsi untuk mengukur kekuatan-. Semakin besar bobot objek, semakin besar perpanjangan pegas, yang diukur pada skala yang disediakan dalam perangkat.

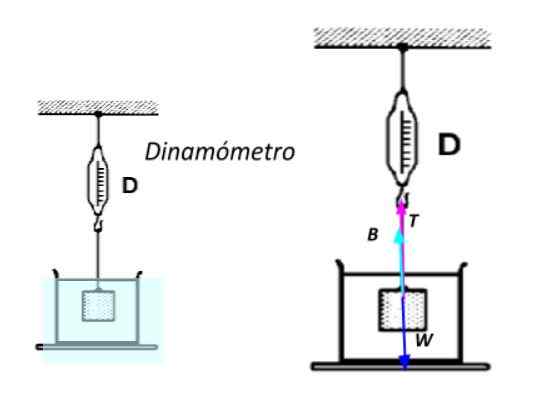Bobot yang jelas dari objek yang terendam. Sumber: disiapkan oleh f. Zapata.

Menerapkan hukum kedua Newton mengetahui bahwa objek sedang istirahat:

Σf_Dan = B + t - w = 0

Berat yang jelas w_ke Itu setara dengan ketegangan pada tali T:

T = w_ke

W_ke = mg - ρ_fasih . V. G

Jika volume V yang terendam diperlukan, itu dihapus sebagai:

V = (w - w_ke ) / ρ_fasih  . G

Demonstrasi

https: // giphy.com/gifs/mcphpppgtnpbhl4cgaq

Ketika tubuh merendam, dorongan adalah kekuatan yang dihasilkan dari semua kekuatan yang diberikan pada tubuh melalui tekanan yang disebabkan oleh cairan di sekitarnya:

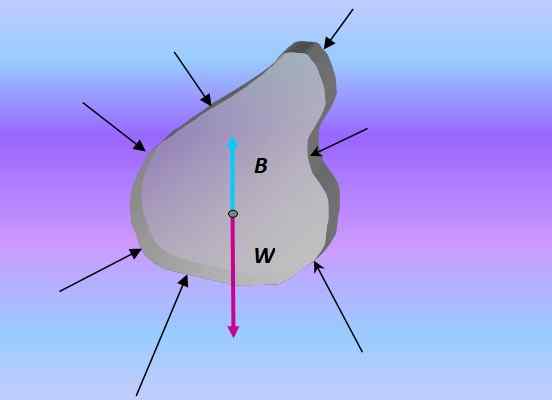Diagram tubuh bebas dari objek yang terendam. Sumber: disiapkan oleh f. Zapata.

Tekanan dan kedalaman

Karena tekanan meningkat dengan kedalaman, hasil dari gaya -kekuatan ini selalu diarahkan secara vertikal ke atas. Oleh karena itu, prinsip Archimedes adalah konsekuensi dari teorema mendasar hidrostatik, yang menghubungkan tekanan yang diberikan oleh cairan dengan kedalaman z sebagai:

P = ρ.G.z

Gaya pada cairan keseimbangan statis

Untuk menunjukkan prinsip Archimedes, bagian istirahat silinder kecil diambil secara istirahat untuk menganalisis gaya yang diberikan di atasnya, seperti yang ditunjukkan pada gambar berikut. Kekuatan pada permukaan melengkung silinder dibatalkan satu sama lain. 

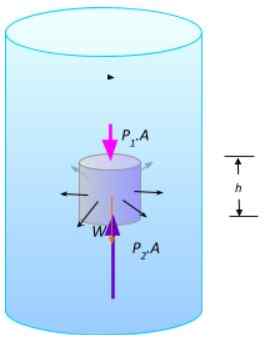Sebagian cairan dalam keseimbangan. Sumber: disiapkan oleh f. Zapata.

Besarnya gaya vertikal adalah F₁ = P₁.A dan F₂ = P2.A, ada beratnya W. Karena cairan seimbang, jumlah kekuatan harus dibatalkan:

∑f_Dan = P₂.A- p₁.A- w = 0

P₂.A- p₁.A = w

Karena dorongan mengkompensasi berat, karena bagian cairan sedang istirahat, maka:

B = p₂.A- p₁.A = w

Dari ekspresi ini mengikuti bahwa dorongan disebabkan oleh perbedaan tekanan antara permukaan atas silinder dan yang lebih rendah. Sebagai W = mg = ρfasih. V. G, Kamu harus:

B = ρ_fasih. V_terendam. G

Yang justru ekspresi untuk dorongan yang disebutkan di bagian sebelumnya.

Aplikasi Prinsip Archimedes

Balon yang mengapung: Prinsip Archimedes sedang beraksi

Prinsip Archimedes muncul dalam banyak aplikasi praktis, di antaranya dapat kami beri nama:

- Balon aerostatik. Yang dengan memiliki kepadatan rata -rata kurang dari udara di sekitarnya, mengapung di dalamnya karena gaya dorong.

- Kapal. Helm kapal lebih berat dari air. Tetapi jika lambung dianggap plus udara di dalam, hasil bagi antara massa total dan volumenya kurang dari air dan itulah alasan mengapa kapal melayang.

- Rompi kehidupan. Saat dibangun dari bahan cahaya dan berpori, mereka dapat mengapung karena rasio volume massa kurang dari air.

- Mengambang untuk menutup keran pengisian tangki air. Ini adalah bola yang penuh dengan udara volume besar yang mengapung di atas air, yang menyebabkan gaya dorong - dikalikan dengan efek tuas - menutup tutup keran pengisian tangki air ketika telah mencapai total level.

Itu dapat melayani Anda: Gelombang Unidimensional: Ekspresi Matematika dan Contoh

Contoh

Contoh 1

Legenda mengatakan bahwa Raja Hierón memberi Goldsmith sejumlah emas untuk membuat mahkota, tetapi raja yang tidak mempercayai itu berpikir bahwa tukang emas bisa berselingkuh ketika menempatkan logam yang kurang berharga di dalam mahkota daripada mahkota. Tapi bagaimana saya bisa tahu tanpa menghancurkan mahkota? 

Raja menugaskan Archimedes dan ini, mencari solusinya, menemukan prinsipnya yang terkenal.

Misalkan mahkota memiliki berat 2,10 kg-f di udara dan 1,95 kg-f saat benar-benar tenggelam dalam air. Dalam hal ini, tidak ada penipuan?

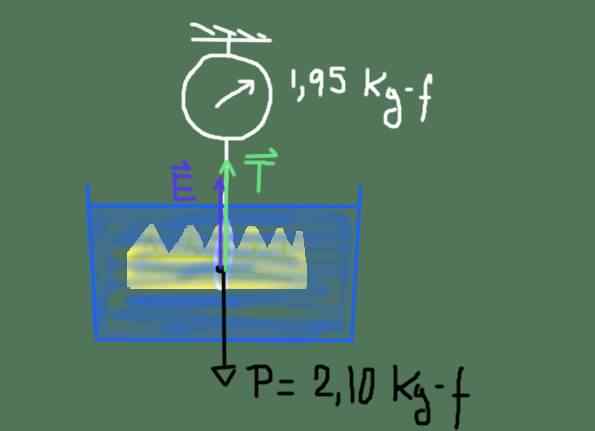Diagram Tubuh Bebas Mahkota King Heron. Sumber: disiapkan oleh f. Zapata

Diagram gaya ditunjukkan pada gambar sebelumnya. Kekuatan -kekuatan ini adalah: beratnya P dari mahkota, dorongan DAN dan ketegangan T dari tali yang menggantung dari skala.

P = 2,10 kg-f dan t = 1,95 kg-f diketahui, perlu untuk menentukan besarnya dorongan DAN:

T + e = p ⇒ e = p - t = (2.10 - 1.95) kg -f = 0.15 kg -f

Di sisi lain, menurut prinsip Archimedes, dorongan itu setara dengan berat air yang diusir ruang yang ditempati oleh mahkota, yaitu kepadatan air dengan volume mahkota karena percepatan gravitasi :

E = ρ_air⋅v⋅g = 1000 kg/m^3 ⋅ V ⋅ 9.8m/s^2 = 0,15 kg ⋅ 9.8 m/s^2

Di mana volume mahkota dapat dihitung:

V = 0,15 kg / 1000 kg / m^3 = 0,00015 m^3

Kepadatan mahkota adalah hasil bagi antara massa mahkota dari air dan volume:

Kepadatan mahkota = 2,10 kg / 0,00015 m^3 = 14000 kg / m^3

Kepadatan emas murni dapat ditentukan oleh prosedur yang sama dan hasilnya adalah tahun 19300 kg/m^3.

Membandingkan dua kepadatan, terbukti bahwa mahkota itu bukan emas murni! 

Contoh 2 

Berdasarkan data dan hasil dari Contoh 1, dimungkinkan untuk menentukan berapa banyak emas yang dicuri oleh Goldsmith dalam kasus bahwa bagian dari emas telah digantikan oleh perak, yang memiliki kepadatan 10500 kg/m^3 3.

Kami akan memanggil ρc ke kepadatan mahkota, ρo ke kepadatan emas dan ρ_P untuk kepadatan perak.

Total massa mahkota adalah:

M = ρc⋅v = ρo⋅vo + ρ_P⋅vp

Volume total mahkota adalah volume perak ditambah volume emas:

V = vo + vp ⇒ vp = v - vo

Mengganti persamaan massa:

ρc⋅v = ρo⋅vo + ρ_P⋅ (v - vo) ⇒ (ρo - ρ_P) Vo = (ρc - ρ_P) V

Artinya volume emas yang berisi mahkota volume total V adalah:

Vo = v⋅ (ρc - ρ_P)/(ρo - ρ_P) = ..

... = 0,00015 m^3 (14000 - 10500)/(19300 - 10500) = 0,0000596 m^3

Untuk mengetahui bobot emas yang berisi mahkota kami melipatgandakan kepadatan emas:

Dapat melayani Anda: aturan tangan kanan

MO = 19300 *0,00005966 = 1.1514 kg

Karena massa mahkota adalah 2,10 kg, kita tahu bahwa 0,94858 kg emas dicuri oleh tukang emas dan digantikan oleh perak.

Latihan terpecahkan

Latihan 1

Balon helium besar mampu mempertahankan keseimbangan (tanpa naik atau turun) kepada seseorang.

Asumsikan bahwa berat orang tersebut, ditambah keranjang, senar dan balon adalah 70 kg. Apa volume helium yang diperlukan untuk ini terjadi? Berapa ukuran yang akan dimiliki balon?

Larutan

Kami akan mengasumsikan bahwa dorongan diproduksi terutama oleh volume helium dan bahwa dorongan komponen lainnya sangat kecil dibandingkan dengan helium yang menempati volume lebih banyak.

Dalam hal ini, volume helium akan diperlukan yang mampu memberikan dorongan berat 70 kg +.

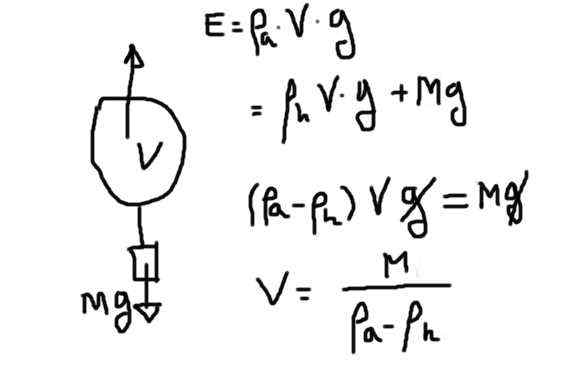Fdiaogram tubuh bebas penuh helium. Sumber: disiapkan oleh f. Zapata.

Dorongan adalah produk volume helium karena kepadatan helium karena percepatan gravitasi. Dorongan itu harus mengimbangi bobot helium ditambah berat sisanya.

Da⋅v⋅g = da⋅v⋅g + m⋅g

di mana ia menyimpulkan bahwa v = m / (da - dh)

V = 70 kg / (1.25 - 0,18) kg/m^3 = 65.4 m^3

Artinya, 65 diperlukan.4 m^3 helium pada tekanan atmosfer untuk dukungan.

Jika kita mengasumsikan balon bola kita dapat menemukan jari -jari yang sama dari hubungan antara volume dan jari -jari bola:

V = (4/3) ⋅π⋅r^3

Dimana r = 2,49 m. Dengan kata lain, diameter 5 m yang penuh helium akan diperlukan.

Latihan 2

Bahan kepadatan yang lebih rendah bahwa air mengapung di tempat yang sama. Asumsikan bahwa Anda memiliki kubus polystyrene (gabus putih), kayu dan es. Kepadatannya dalam kg per meter kubik masing -masing: 20, 450 dan 915.

Temukan fraksi volume total apa yang keluar dari air dan tingginya apa yang menonjol sehubungan dengan permukaan air yang diambil sebagai kepadatan 1000 kilogram terakhir per meter kubik.

Larutan 

Kemampuan mengapung terjadi ketika berat badan sama dengan dorong karena air:

E = m⋅g

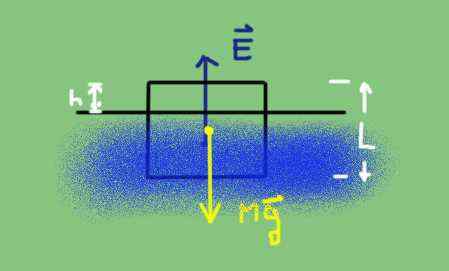Diagram tubuh bebas dari objek yang terendam sebagian. Sumber: disiapkan oleh f. Zapata.

Berat adalah kepadatan tubuh DC dikalikan dengan volume V dan dengan percepatan gravitasi g.

Dorongan adalah berat cairan yang dipindahkan sesuai dengan prinsip Archimedes dan dihitung dengan mengalikan kepadatan D air dengan volume V yang terendam dan dengan percepatan gravitasi.

Itu adalah:

D⋅v'⋅g = dc⋅v⋅g

Yang berarti bahwa fraksi volume yang terendam sama dengan hasil bagi antara kepadatan tubuh dan kepadatan air.

(V '/v) = (dc/d) 

Artinya fraksi volume yang luar biasa (v "/v) adalah

(V "/v) = 1 - (dc/d)

Ya H Itu adalah ketinggian yang luar biasa dan L Sisi kubus fraksi volume dapat ditulis sebagai

(H⋅l^2)/(l^3) = h/l, Dengan kata lain, fraksi tinggi yang luar biasa juga

(h/l) = 1 - (dc/d)

Maka hasil untuk materi yang diminta adalah:

Polystyrene (White Cork):

(H/l) = (v "/v) = 1 - (dc/d) = 1- (20/1000) = 98% terlepas dari air

Kayu:

(h/l) = (v "/v) = 1 - (dc/d) = 1- (450/1000) = 55% terlepas dari air

Es:

(h/l) = (v "/v) = 1 - (dc/d) = 1- (915/1000) = 8.5% terlepas dari air

Referensi

1. Bauer, w. 2011. Fisika untuk Teknik dan Ilmu Pengetahuan. Volume 1. MC Graw Hill. 417-455.
2. Cengel Y, Cimbala J. 2011.Mekanika Cairan. Fundamental dan Aplikasi. Edisi pertama. Bukit McGraw.
3. Figueroa, d. (2005). Seri: Fisika untuk Sains dan Teknik. Volume 4. Cairan dan termodinamika. Diedit oleh Douglas Figueroa (USB). 1 - 42.
4. Giles, r. 2010. Mekanika cairan dan hidrolik. Bukit McGraw. 
5. Rex, a. 2011. Dasar -dasar fisika. Pearson. 239-263.
6. Tippens, hlm. 2011. Fisika: Konsep dan Aplikasi. Edisi ke -7. Bukit McGraw.