Karakteristik prisma pentagonal, bagian, simpul, tepi, volume

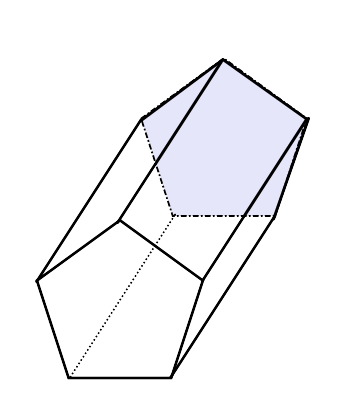
A Prisma pentagonal Ini adalah sosok geometris tiga dimensi yang pangkalannya, identik, memiliki bentuk pentagon, dan juga memiliki total 5 -sisi dalam bentuk jajaran genjang.

Jika wajahnya persegi panjang dikatakan bahwa itu adalah a Prisma pentagonal lurus, Sementara jika ujungnya cenderung ke pangkalan, maka itu adalah a Prisma pentagonal miring. Pada gambar berikut ada contoh masing -masing.

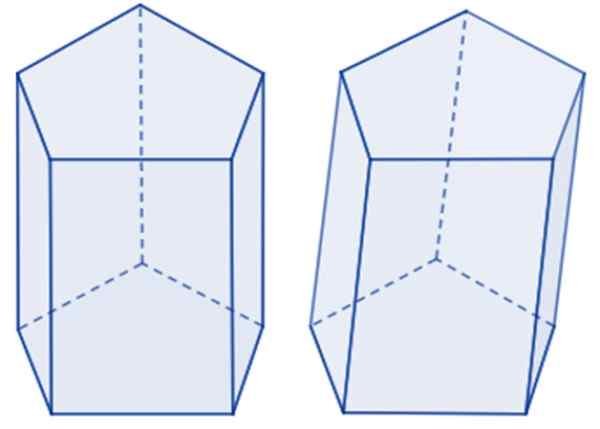Prisma pentagonal ke kiri dan miring ke kanan. Sumber: Wikimedia Commons.

Pentagon dasar bisa teratur jika kelima sisi memiliki ukuran yang sama, serta sudut internal, jika tidak, itu adalah pentagon yang tidak teratur. Jika basis prisma teratur, itu tentang Prisma pentagonal biasa. Kalau tidak adalah prisma Pentagonal tidak teratur.

Prisma pentagonal dasar yang tidak teratur digunakan dalam konstruksi modern. Sumber: Wallpaper Flare.

Prisma pentagonal adalah struktur harmonis yang digunakan dalam arsitektur dan desain benda, seperti bangunan modern yang ditunjukkan pada sosok atas. Jendela berbentuk Pentagon yang tidak teratur membentuk dasar prisma.

[TOC]

Karakteristik prisma pentagonal

-Ini adalah angka geometris tiga dimensi, permukaan yang menyusunnya mengandung volume tertentu.

-Basis mereka adalah pentagon dan wajah sampingnya bisa berupa persegi panjang atau jajaran genjang.

-Ia memiliki simpul -sudut pandang prisma -dan tepi atau pantai-.

-Jika tepi yang menyatukan pangkalan tegak lurus terhadap mereka, prisma lurus, dan jika cenderung, prisma itu miring.

-Saat alasnya adalah pentagon yang sudut internalnya kurang dari 180º, prisma itu cembung, Tetapi jika satu atau lebih sudut internal lebih besar dari 180º, itu adalah prisma cekung.

Elemen prisma pentagonal

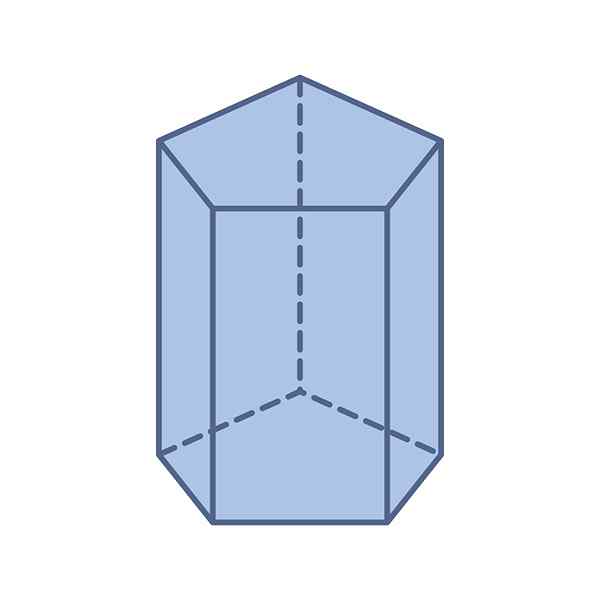
-Pangkalan: Ia memiliki dua pangkalan pentagonal dan kongruen -pengukuran mereka sama -baik reguler atau tidak teratur.

Dapat melayani Anda: Formula Umum: Persamaan Kuadratik, Contoh, Latihan

-Wajah: Prisma pentagonal memiliki total 7 wajah: dua pangkalan pentagonal dan lima jajaran genjang yang membentuk sisi.

-Tepian: Segmen yang bergabung dengan dua pangkalan, ditunjukkan dengan warna merah pada Gambar 3 atau satu yang bergabung dengan dua sisi.

-Tinggi: Jarak antara wajah. Jika prisma lurus, jarak ini bertepatan dengan ukuran tepi.

-Puncak: Titik umum antara dasar dan dua sisi sisi.

Gambar yang lebih rendah menunjukkan prisma pentagonal dasar biasa, di mana segmen yang membentuk basis memiliki ukuran yang sama, disebut ke.

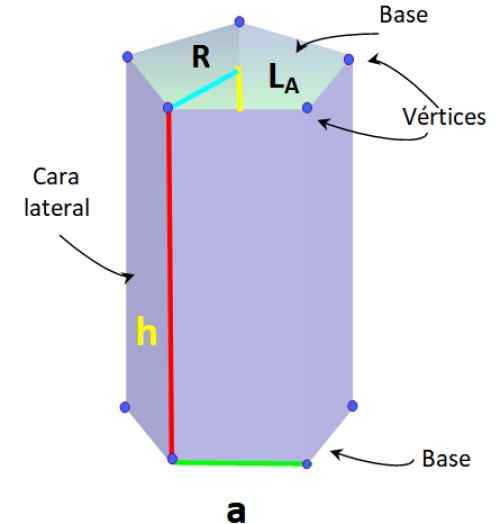 Elemen prisma pentagonal biasa. Sumber: f. Zapata.

Jenis prisma ini juga memiliki elemen -elemen berikut, khas dari Pentagon biasa:

-Radio r: Jarak antara pusat Pentagon dan salah satu simpul.

-Apothem l_KE: segmen yang bergabung dengan pusat dengan titik tengah salah satu sisi Pentagon.

Berapa banyak simpul yang dimiliki prisma pentagonal?

Di Pentagon ada 5 simpul dan karena prisma pentagonal memiliki dua pentagon sebagai pangkalan, tubuh ini memiliki total 10 simpul.

Berapa banyak tepi yang dimiliki prisma pentagonal?

Anda dapat menghitung jumlah tepi untuk tubuh geometris dengan wajah datar, seperti prisma, menggunakan Teorema Euler Untuk cembung polyhedros. Leonhard Euler (1707-1783) adalah salah satu ahli matematika dan fisik terbesar dalam sejarah.

Teorema menetapkan hubungan antara jumlah wajah, yang akan kita sebut C, jumlah simpul V dan tepi total A sebagai berikut:

C+V = A+2

Untuk prisma pentagonal yang kita miliki: c = 7 dan v = 10. Membersihkan, jumlah tepi:

Itu dapat melayani Anda: fungsi bijyjective: apa itu, bagaimana cara melakukannya, contoh, latihan

A = C+V-2

Mengganti Nilai:

A = 7 + 10 - 2 = 15

Prisma pentagonal memiliki 15 tepi.

Bagaimana mendapatkan volume prisma pentagonal?

Volume prisma pentagonal mengukur ruang yang terkunci oleh sisi dan pangkalan. Ini adalah jumlah positif yang dihitung dengan properti berikut:

Pesawat apa pun yang memotong prisma tegak lurus dengan ujung -ujungnya, menghasilkan persimpangan dengan cara yang sama seperti pangkalan, yaitu, pentagon dari dimensi yang sama.

Oleh karena itu, volume prisma pentagonal adalah produk dari area dasar dan ketinggian prisma.

Menjadi KE_B area dasar pentagonal dan H Ketinggian prisma, lalu volume V adalah:

V = a_B x h

Formula ini bersifat umum, valid untuk prisma apa pun, baik secara teratur atau tidak teratur, lurus atau miring.

Volume prisma selalu datang dalam satuan panjang tinggi ke kubus. Jika panjang sisi dan ketinggian prisma diberikan dalam meter, maka volume dinyatakan dalam m³, "Meter kubik" itu dibaca. Unit lainnya termasuk CM³, km³, inci³ dan lebih banyak lagi.

- Volume prisma pentagonal biasa

Dalam prisma pentagonal reguler, pangkalan adalah pentagon biasa, yang berarti bahwa sisi dan sudut internal adalah sama. Mengingat simetri tubuh, area Pentagon dan oleh karena itu volume mudah dihitung dalam beberapa cara:

Mengetahui tinggi dan pengukuran sisi

Menjadi ke Ukuran sisi dasar pentagonal. Dalam hal ini area tersebut dihitung oleh:

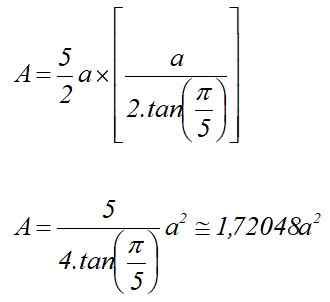
Oleh karena itu volume prisma pentagonal reguler tinggi h adalah:

Dapat melayani Anda: Nomor Imajiner: Properti, Aplikasi, Contoh

V = 1.72048 a²⋅ H

Mengetahui tinggi dan ukuran radio

Ketika Radio r Dari basis pentagonal, persamaan lain ini dapat digunakan untuk area dasar:

A = (5/2) r²⋅ Sen 72º

Dengan cara ini volume prisma pentagonal diberikan oleh:

V = (5/2) r² ⋅ H ⋅ sen 72º

Di mana H Itu adalah ketinggian prisma

Mengetahui ketinggian, ukuran nilai apothem dan perimeter

Area dasar pentagonal dapat dihitung jika perimeter P diketahui, yang merupakan jumlah sisi, serta ukuran apothem l l_KE:

A = p. L_KE / 2

Mengalikan ekspresi ini dengan nilai tinggi H, Kami memiliki volume prisma:

V = P. L_KE .H / 2

- Volume prisma pentagonal yang tidak teratur

Formula yang diberikan pada awalnya bahkan valid ketika dasar prisma adalah pentagon yang tidak teratur:

V = a_B x h

Untuk menghitung area dasar, berbagai metode digunakan, misalnya:

-Metode triangulasi, yang terdiri dari membagi pentagon menjadi segitiga dan segi empat, yang area masing -masing mudah dihitung. Area Pentagon akan menjadi jumlah area dari angka -angka yang lebih sederhana ini.

-Metode penentu Gauss, yang harus Anda ketahui simpul sosok.

Setelah nilai area ditentukan, itu dikalikan dengan ketinggian prisma untuk mendapatkan volume.

Referensi

1. Alexander, d. 2013. Geometri. Ke -5. Edisi. Pembelajaran Cengage.
2. Referensi Terbuka Matematika. Area Poligon. Pulih dari: mathpenref.com.
3. Rumus alam semesta. Teorema Euler untuk polyhedros. Pulih dari: universoformulas.com.
4. Rumus alam semesta. Area pentagon biasa. Pulih dari: universoformulas.com.
5. Wikipedia. Prisma. Pulih dari: is.Wikipedia.com.
6. Wikipedia. Prisma pentagonal. Pulih dari: is.Wikipedia.com.